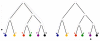The evolution of domain-content in bacterial genomes - PubMed (original) (raw)
The evolution of domain-content in bacterial genomes
Nacho Molina et al. Biol Direct. 2008.
Abstract
Background: Across all sequenced bacterial genomes, the number of domains nc in different functional categories c scales as a power-law in the total number of domains n, i.e. nc proportional n(alpha)c, with exponents alpha(c) that vary across functional categories. Here we investigate the implications of these scaling laws for the evolution of domain-content in bacterial genomes and derive the simplest evolutionary model consistent with these scaling laws.
Results: We show that, using only an assumption of time invariance, the scaling laws uniquely determine the relative rates of domain additions and deletions across all functional categories and evolutionary lineages. In particular, the model predicts that the rate of additions and deletions of domains of category c is proportional to the number of domains nc currently in the genome and we discuss the implications of this observation for the role of horizontal transfer in genome evolution. Second, in addition to being proportional to nc, the rate of additions and deletions of domains of category c is proportional to a category-dependent constant rho(c), which is the same for all evolutionary lineages. This 'evolutionary potential' rho(c) represents the relative probability for additions/deletions of domains of category c to be fixed in the population by selection and is predicted to equal the scaling exponent alpha(c). By comparing the domain content of 93 pairs of closely-related genomes from all over the phylogenetic tree of bacteria, we demonstrate that the model's predictions are supported by available genome-sequence data.
Conclusion: Our results establish a direct quantitative connection between the scaling of domain numbers with genome size, and the rate of addition and deletions of domains during short evolutionary time intervals.of domain numbers with genome size, and the rate of addition and deletions of domains during short evolutionary time intervals.
Figures
Figure 1
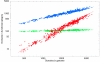
Scaling laws. The number of protein-domains associated with functional categories 'translation' (green), metabolic process' (blue), and 'regulation of transcription' (red) as a function of the total number of domains in the genome for which a functional annotation is available. Each dot corresponds to a fully-sequenced microbial genome, with the total number of domains on the horizontal axis and the number of domains in a particular functional category on the vertical axis. Both axes are shown on a logarithmic scale. The straight lines show power-law fits.
Figure 2
Evolutionary histories and time invariance. Evolutionary histories of different organisms. The scaling laws constrain integrals of domain-count changes over long evolutionary times, i.e. from the common ancestor up to the present (left panel). Our assumption of time invariance now implies relations between the domain-count changes during short time intervals which can be tested by comparing domain-counts in closely-related genomes (right panel).
Figure 3
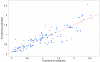
Linear dependence of domain-count changes on domain occurrence. Linear dependency of the fraction of domain-count changes on the domain-count itself. Left panel : For each genome pair i the fraction Δnci/Δni of domain-count changes that involve domains of category c is shown (vertical axis) as a function of the fraction nci/ni of all domains in the genome that are associated with category c (horizontal axis) for the categories 'metabolic process' (blue), 'regulation of transcription' (red), and 'protein kinase activity' (green). Each dot corresponds to the data for one pair i of closely-related genomes. Both axes are shown on a logarithmic scale. The straight-lines show least-squares fits of the form log[Δnci/Δni]=γclog[nci/ni]+δc. The fitted slopes for the three categories are _γ_prot.kin.activity = 0.56 ± 0.46, _γ_reg.transcr. = 0.95 ± 0.20, and _a_met.proc. = 1.48 ± 0.31. For comparison the dotted lines show linear scaling. Right panel: A 99% posterior probability interval for the slope γ c was estimated for all selected GO categories (Methods). The fitted slopes were ordered from high to low and are shown in the right panel from left to right with the vertical bars corresponding to the 99% posterior probability intervals for each slope γ c. The slope γ = 1, corresponding to a linear dependency, is shown as a horizontal dotted line.
Figure 4
Evolutionary potentials across different lineages. Distribution of inferred evolutionary potentials ρci for the categories 'translation' (left panel), 'metabolic process' (middle panel), and 'regulation of transcription' (right panel) across all genome pairs i. Each panel shows the 99% posterior probability intervals [lci,hci] for the potentials ρci as vertical bars (sorted from left to right by their means). The dotted horizontal lines show the average ρci, averaged over all pairs i.
Figure 5
Correlation between exponents α c and evolutionary potentials ρ c. Correlation between the inferred evolutionary potentials ρ c (vertical axis) and the exponents ρ c (horizontal axis) of the scaling laws. Each dot corresponds to one of the 156 selected GO categories. The line shows the linear fit ρ c = 0.71_α_ c + 0.1 with correlation coefficient _r_2 = 0.80.
Similar articles
- Family-specific scaling laws in bacterial genomes.
De Lazzari E, Grilli J, Maslov S, Cosentino Lagomarsino M. De Lazzari E, et al. Nucleic Acids Res. 2017 Jul 27;45(13):7615-7622. doi: 10.1093/nar/gkx510. Nucleic Acids Res. 2017. PMID: 28605556 Free PMC article. - Joint scaling laws in functional and evolutionary categories in prokaryotic genomes.
Grilli J, Bassetti B, Maslov S, Cosentino Lagomarsino M. Grilli J, et al. Nucleic Acids Res. 2012 Jan;40(2):530-40. doi: 10.1093/nar/gkr711. Epub 2011 Sep 21. Nucleic Acids Res. 2012. PMID: 21937509 Free PMC article. - Algorithms for computing parsimonious evolutionary scenarios for genome evolution, the last universal common ancestor and dominance of horizontal gene transfer in the evolution of prokaryotes.
Mirkin BG, Fenner TI, Galperin MY, Koonin EV. Mirkin BG, et al. BMC Evol Biol. 2003 Jan 6;3:2. doi: 10.1186/1471-2148-3-2. Epub 2003 Jan 6. BMC Evol Biol. 2003. PMID: 12515582 Free PMC article. - Phylogenomic networks.
Dagan T. Dagan T. Trends Microbiol. 2011 Oct;19(10):483-91. doi: 10.1016/j.tim.2011.07.001. Epub 2011 Aug 3. Trends Microbiol. 2011. PMID: 21820313 Review.
Cited by
- Evolution of biomolecular networks: lessons from metabolic and protein interactions.
Yamada T, Bork P. Yamada T, et al. Nat Rev Mol Cell Biol. 2009 Nov;10(11):791-803. doi: 10.1038/nrm2787. Nat Rev Mol Cell Biol. 2009. PMID: 19851337 Review. - Family-specific scaling laws in bacterial genomes.
De Lazzari E, Grilli J, Maslov S, Cosentino Lagomarsino M. De Lazzari E, et al. Nucleic Acids Res. 2017 Jul 27;45(13):7615-7622. doi: 10.1093/nar/gkx510. Nucleic Acids Res. 2017. PMID: 28605556 Free PMC article. - Large-scale dynamics of horizontal transfers.
Grassi L, Grilli J, Lagomarsino MC. Grassi L, et al. Mob Genet Elements. 2012 May 1;2(3):163-167. doi: 10.4161/mge.21112. Mob Genet Elements. 2012. PMID: 23061026 Free PMC article. - On the origin of protein superfamilies and superfolds.
Magner A, Szpankowski W, Kihara D. Magner A, et al. Sci Rep. 2015 Feb 23;5:8166. doi: 10.1038/srep08166. Sci Rep. 2015. PMID: 25703447 Free PMC article. - Modular origins of biological electron transfer chains.
Raanan H, Pike DH, Moore EK, Falkowski PG, Nanda V. Raanan H, et al. Proc Natl Acad Sci U S A. 2018 Feb 6;115(6):1280-1285. doi: 10.1073/pnas.1714225115. Epub 2018 Jan 22. Proc Natl Acad Sci U S A. 2018. PMID: 29358375 Free PMC article.
References
- Zuckerkandl E, Pauling LB. Molecular disease, evolution, and genetic heterogeneity. In: Kasha M, Pulman B, editor. Horizons in Biochemistry. New York: Academic Press; 1962. pp. 189–225.
- Kimura M. The Neutral Theory of Molecular Evolution. Cambridge University Press; 1983.
- Nei M, Gojobori T. Simple methods for estimating the numbers of synonymous and nonsynonymous nucleotide substitutions. Molecular Biology and Evolution. 1986;3:418–426. - PubMed
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources