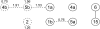A model selection approach for the identification of quantitative trait loci in experimental crosses, allowing epistasis - PubMed (original) (raw)
A model selection approach for the identification of quantitative trait loci in experimental crosses, allowing epistasis
Ani Manichaikul et al. Genetics. 2009 Mar.
Erratum in
- Genetics. 2010 Feb;184(2):607
Abstract
The identification of quantitative trait loci (QTL) and their interactions is a crucial step toward the discovery of genes responsible for variation in experimental crosses. The problem is best viewed as one of model selection, and the most important aspect of the problem is the comparison of models of different sizes. We present a penalized likelihood approach, with penalties on QTL and pairwise interactions chosen to control false positive rates. This extends the work of Broman and Speed to allow for pairwise interactions among QTL. A conservative version of our penalized LOD score provides strict control over the rate of extraneous QTL and interactions; a more liberal criterion is more lenient on interactions but seeks to maintain control over the rate of inclusion of false loci. The key advance is that one needs only to specify a target false positive rate rather than a prior on the number of QTL and interactions. We illustrate the use of our model selection criteria as exploratory tools; simulation studies demonstrate reasonable power to detect QTL. Our liberal criterion is comparable in power to two Bayesian approaches.
Figures
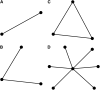
Figure 1.—
Example graphical representations of QTL models. Nodes represent QTL and edges represent pairwise interactions. (A) A model containing two QTL and their interaction. (B) A model containing three QTL and two pairwise interactions. (C) A model containing three QTL and all possible pairwise interactions. (D) A model containing seven QTL, with one central locus interacting with the other six.
Figure 2.—
The final model for hypertension data in S
ugiyama
et al. (2001) contained a pair of QTL on chromosome 1, unlinked QTL on chromosomes 4 and 5, and a pair of interacting QTL on chromosomes 6 and 15 (solid line). We explored the possibility of additional interactions between QTL in the original model of S
ugiyama
et al. (2001) and also considered additional QTL on chromosomes 2, 4, and 5, with possible interactions involving these loci (dashed lines). Each new model term is annotated with its corresponding contribution to the model LOD score. For example, an interaction between model terms 1b and 5a increased the model LOD score by 0.76 compared to the original model.
Figure 3.—
Estimated error rates for intercross simulations under a model based on data from S
mith
R
ichards
et al. (2002). Plots display observed distribution summaries of (A) the number of extraneous main effects, (B) the number of extraneous interactions, (C) the number of interactions associated with extraneous main effects, and (D) the probability of one or more extraneous unlinked terms as a function of the number of correct main effects, shown only when at least 30 simulation replicates had the specified number of correct main effects using a given method. Ninety-five percent confidence intervals in D are obtained by inverting an exact binomial test. Results are shown for pLODL (solid black circle), pLODH (solid red square), pLODa (solid blue triangle), Bayes (open black diamond), mBIC2 (open black circle), and mBIC1 (open red square).
Figure 4.—
Estimated power to detect true QTL in intercross simulations under a model based on data from S
mith
R
ichards
et al. (2002). Plots display (A) the power to detect each individual model term, (B) the heritability of the QTL main effects and interactions, (C) the root mean squared error of the estimated positions among correctly identified QTL, and (D) the observed distribution of the number of correct main effects identified in each simulation replicate. A, C, and D show results for pLODL (solid black circle), pLODH (solid red square), pLODa (solid blue triangle), Bayes (open black diamond), mBIC2 (open black circle), and mBIC1 (open red square).
Similar articles
- Bayesian model selection for genome-wide epistatic quantitative trait loci analysis.
Yi N, Yandell BS, Churchill GA, Allison DB, Eisen EJ, Pomp D. Yi N, et al. Genetics. 2005 Jul;170(3):1333-44. doi: 10.1534/genetics.104.040386. Epub 2005 May 23. Genetics. 2005. PMID: 15911579 Free PMC article. - A two-step approach to map quantitative trait loci for meat quality in connected porcine F(2) crosses considering main and epistatic effects.
Stratz P, Baes C, Rückert C, Preuss S, Bennewitz J. Stratz P, et al. Anim Genet. 2013 Feb;44(1):14-23. doi: 10.1111/j.1365-2052.2012.02360.x. Epub 2012 Apr 18. Anim Genet. 2013. PMID: 22509991 - Efficiency of triple test cross for detecting epistasis with marker information.
Zhu C, Zhang R. Zhu C, et al. Heredity (Edinb). 2007 Jun;98(6):401-10. doi: 10.1038/sj.hdy.6800956. Epub 2007 Mar 28. Heredity (Edinb). 2007. PMID: 17392709 - QTL-based evidence for the role of epistasis in evolution.
Malmberg RL, Mauricio R. Malmberg RL, et al. Genet Res. 2005 Oct;86(2):89-95. doi: 10.1017/S0016672305007780. Genet Res. 2005. PMID: 16356282 Review. - QTL mapping and the genetic basis of adaptation: recent developments.
Zeng ZB. Zeng ZB. Genetica. 2005 Feb;123(1-2):25-37. doi: 10.1007/s10709-004-2705-0. Genetica. 2005. PMID: 15881678 Review.
Cited by
- Identification of powdery mildew resistance quantitative trait loci in melon and development of resistant near-isogenic lines through marker-assisted backcrossing.
Wang CS, Lin SY, Huang JH, Chang HY, Lew DK, Wang YH, Hwu KK, Huang YF. Wang CS, et al. Bot Stud. 2024 Nov 4;65(1):31. doi: 10.1186/s40529-024-00435-x. Bot Stud. 2024. PMID: 39495375 Free PMC article. - An ultra-dense linkage map identified quantitative trait loci corresponding to fruit quality- and size-related traits in red goji berry.
Rehman F, Gong H, Ma Y, Zeng S, Ke D, Yang C, Zhao Y, Wang Y. Rehman F, et al. Front Plant Sci. 2024 Sep 4;15:1390936. doi: 10.3389/fpls.2024.1390936. eCollection 2024. Front Plant Sci. 2024. PMID: 39297015 Free PMC article. - Wheat (Triticum aestivum) chromosome 6D harbours the broad spectrum common bunt resistance gene Bt11.
Lunzer M, Buerstmayr M, Grausgruber H, Müllner AE, Fallbacher I, Buerstmayr H. Lunzer M, et al. Theor Appl Genet. 2023 Sep 7;136(9):207. doi: 10.1007/s00122-023-04452-5. Theor Appl Genet. 2023. PMID: 37679535 Free PMC article. - Genetics of evolved load resistance in the skeletons of unusually large mice from Gough Island.
Payseur BA, Anderson S, James RT, Parmenter MD, Gray MM, Vinyard CJ. Payseur BA, et al. Genetics. 2023 Aug 31;225(1):iyad137. doi: 10.1093/genetics/iyad137. Genetics. 2023. PMID: 37477896 Free PMC article. - Genomic regions associated with chocolate spot (Botrytis fabae Sard.) resistance in faba bean (Vicia faba L.).
Gela TS, Bruce M, Chang W, Stoddard FL, Schulman AH, Vandenberg A, Khazaei H. Gela TS, et al. Mol Breed. 2022 Jun 22;42(6):35. doi: 10.1007/s11032-022-01307-7. eCollection 2022 Jun. Mol Breed. 2022. PMID: 37312967 Free PMC article.
References
- Akaike, H., 1969. Fitting autoregressive models for prediction. Ann. Inst. Stat. Math. 21 243–247.
Publication types
MeSH terms
Grants and funding
- GM069430/GM/NIGMS NIH HHS/United States
- GM078338/GM/NIGMS NIH HHS/United States
- R01 GM078338/GM/NIGMS NIH HHS/United States
- GM074244/GM/NIGMS NIH HHS/United States
- R01 GM069430/GM/NIGMS NIH HHS/United States
- R01 GM074244/GM/NIGMS NIH HHS/United States
LinkOut - more resources
Full Text Sources