Synaptic depression enables neuronal gain control - PubMed (original) (raw)
. 2009 Feb 19;457(7232):1015-8.
doi: 10.1038/nature07604. Epub 2009 Jan 14.
Affiliations
- PMID: 19145233
- PMCID: PMC2689940
- DOI: 10.1038/nature07604
Synaptic depression enables neuronal gain control
Jason S Rothman et al. Nature. 2009.
Abstract
To act as computational devices, neurons must perform mathematical operations as they transform synaptic and modulatory input into output firing rate. Experiments and theory indicate that neuronal firing typically represents the sum of synaptic inputs, an additive operation, but multiplication of inputs is essential for many computations. Multiplication by a constant produces a change in the slope, or gain, of the input-output relationship, amplifying or scaling down the sensitivity of the neuron to changes in its input. Such gain modulation occurs in vivo, during contrast invariance of orientation tuning, attentional scaling, translation-invariant object recognition, auditory processing and coordinate transformations. Moreover, theoretical studies highlight the necessity of gain modulation in several of these tasks. Although potential cellular mechanisms for gain modulation have been identified, they often rely on membrane noise and require restrictive conditions to work. Because nonlinear components are used to scale signals in electronics, we examined whether synaptic nonlinearities are involved in neuronal gain modulation. We used synaptic stimulation and the dynamic-clamp technique to investigate gain modulation in granule cells in acute slices of rat cerebellum. Here we show that when excitation is mediated by synapses with short-term depression (STD), neuronal gain is controlled by an inhibitory conductance in a noise-independent manner, allowing driving and modulatory inputs to be multiplied together. The nonlinearity introduced by STD transforms inhibition-mediated additive shifts in the input-output relationship into multiplicative gain changes. When granule cells were driven with bursts of high-frequency mossy fibre input, as observed in vivo, larger inhibition-mediated gain changes were observed, as expected with greater STD. Simulations of synaptic integration in more complex neocortical neurons suggest that STD-based gain modulation can also operate in neurons with large dendritic trees. Our results establish that neurons receiving depressing excitatory inputs can act as powerful multiplicative devices even when integration of postsynaptic conductances is linear.
Figures
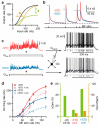
Figure 1. Synaptic depression enhances inhibition-mediated gain modulation
a, Hypothetical neuronal input-output relation before (black) and after multiplicative gain modulation (green, ×) and an additive offset (orange, +). b, Averaged AMPAR-mediated synaptic train exhibiting STD (blue trace) in response to Poisson stimulation (black ticks; f = 86 Hz) of single MF inputs. Red trace shows corresponding artificial synaptic train without STD. c, The sum of 4 independent synaptic trains (each f = 86 Hz) with and without STD injected into a GC via dynamic clamp (_G_clamp) with and without tonic inhibition (black and gray; _G_inh = 500 pS). Right vertical ticks indicate spike times. Horizontal bars indicate output rate measurement window. _V_rest = −79 mV. d, Average input-output relations (n = 9) with and without STD (blue and red) and tonic inhibition (open and closed symbols). Lines are fits to a Hill function (Eq. 5; Supplementary Table 1). e, Gain (green) and offset (orange) changes due to STD (±STD) and inhibition (±inh) from fits in d.
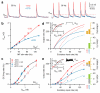
Figure 2. Synaptic depression transforms additive shifts into multiplicative gain modulation
a, Average AMPAR-mediated synaptic trains with and without STD (blue and red) with their time-averaged conductances (_G_exc, dashed lines). b, _G_exc versus MF rate f with and without STD. Red line is a linear fit (Eq. 3). Blue line is an exponential fit (Eq. 4). c, Data in Fig. 1d plotted as output rate (F) versus _G_exc. Lines are Hill fits (Eq. 5). d, Predicted input-output relations computed from G_exc_f relations in b, and experimentally measured GC _FG_exc relation generated with noise-free excitatory conductance steps (inset, red squares from Fig. 2b in ref. 13). Solid line in inset is a Hill fit, and dashed line is the same curve rightward shifted 0.3 nS along the _G_exc-axis. Bar graphs show changes in gain (green) and offset (orange) due to inhibition with and without STD. e, Same as d, except control _FG_exc data (inset) is from c during noisy synaptic excitation. The predicted change in the input-output relation for STD match the experimental observations (blue symbols). Grey bars show gain and offset changes for a leftward shift of 0.3 nS to simulate excitation.
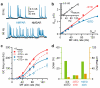
Figure 3. Gain modulation in the presence of synaptic NMDAR conductances
a, Average AMPAR (blue) and NMDAR (black) synaptic conductance trains from the same 4 GCs during Poisson stimulation of individual MF inputs. b, _G_exc versus MF rate (f) for AMPAR+NMDAR components with and without AMPAR STD. Red and blue lines are fits to Eqs. 3 and 4. Inset: G_exc_f relations for NMDAR with and without AMPAR STD (circles and squares). c, Average input-output relations for AMPAR+NMDAR with and without AMPAR STD and tonic inhibition. Lines are Hill fits (Eq. 5). d, Gain (green) and offset (orange) changes due to STD (±STD) and tonic inhibition (±inh) from fits in c.
Figure 4. Gain modulation during broad bandwidth single mossy fibre stimulation
a, Mixed AMPAR+NMDAR EPSCs in GCs during single MF, Poisson burst-like stimulation (black ticks) at −75mV. Stimulus artifacts subtracted. b, Voltage responses to burst-like MF stimulation with and without tonic inhibition (±inh; black and gray; _G_inh = 500 pS) injected via dynamic clamp. Black horizontal bar indicates firing rate measurement window. _V_rest = −74mV. c, Average GC input-output relation ±inh for single MF stimulation (n = 7) with Hill fits (Eq. 5). d, Mean between relationship _G_exc and MF stimulation rate (f). Blue line is an exponential fit (Eq. 4). e, Gain (green) and offset (orange) changes due to inhibition (±inh) computed from fits in c.
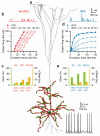
Figure 5. Multiplicative gain modulation in a cortical layer 5 pyramidal neuron model
a, Layer 5 neuron model with location of excitatory (red circles) and inhibitory (green) synaptic contacts. Bottom: black trace shows spiking during synaptic excitation and inhibition. b, Top: conductance train for non-depressing unitary excitatory synaptic input. Bottom: input-output relation for non-depressing synaptic excitation (−STD, red) for control conditions (solid symbols) and various rates of synaptic inhibition (open symbols) together with Hill fits (Eq. 5). c, Gain (green) and offset (orange) changes due to different inhibition rates (±inh) in absence of STD from fits in b. d, As for b, but for depressing synaptic excitation (+STD, blue) together with Hill fits. e, As for c, but for depressing synaptic excitation (+STD) from fits in d.
Similar articles
- Passive Synaptic Normalization and Input Synchrony-Dependent Amplification of Cortical Feedback in Thalamocortical Neuron Dendrites.
Connelly WM, Crunelli V, Errington AC. Connelly WM, et al. J Neurosci. 2016 Mar 30;36(13):3735-54. doi: 10.1523/JNEUROSCI.3836-15.2016. J Neurosci. 2016. PMID: 27030759 Free PMC article. - Properties of excitatory synaptic connections mediated by the corpus callosum in the developing rat neocortex.
Kumar SS, Huguenard JR. Kumar SS, et al. J Neurophysiol. 2001 Dec;86(6):2973-85. doi: 10.1152/jn.2001.86.6.2973. J Neurophysiol. 2001. PMID: 11731554 - A Slow Short-Term Depression at Purkinje to Deep Cerebellar Nuclear Neuron Synapses Supports Gain-Control and Linear Encoding over Second-Long Time Windows.
Pedroarena CM. Pedroarena CM. J Neurosci. 2020 Jul 29;40(31):5937-5953. doi: 10.1523/JNEUROSCI.2078-19.2020. Epub 2020 Jun 17. J Neurosci. 2020. PMID: 32554551 Free PMC article. - The neuronal transfer function: contributions from voltage- and time-dependent mechanisms.
Cook EP, Wilhelm AC, Guest JA, Liang Y, Masse NY, Colbert CM. Cook EP, et al. Prog Brain Res. 2007;165:1-12. doi: 10.1016/S0079-6123(06)65001-2. Prog Brain Res. 2007. PMID: 17925236 Review. - Neuronal arithmetic.
Silver RA. Silver RA. Nat Rev Neurosci. 2010 Jul;11(7):474-89. doi: 10.1038/nrn2864. Nat Rev Neurosci. 2010. PMID: 20531421 Free PMC article. Review.
Cited by
- Location-dependent effects of inhibition on local spiking in pyramidal neuron dendrites.
Jadi M, Polsky A, Schiller J, Mel BW. Jadi M, et al. PLoS Comput Biol. 2012;8(6):e1002550. doi: 10.1371/journal.pcbi.1002550. Epub 2012 Jun 14. PLoS Comput Biol. 2012. PMID: 22719240 Free PMC article. - Short term synaptic depression imposes a frequency dependent filter on synaptic information transfer.
Rosenbaum R, Rubin J, Doiron B. Rosenbaum R, et al. PLoS Comput Biol. 2012;8(6):e1002557. doi: 10.1371/journal.pcbi.1002557. Epub 2012 Jun 21. PLoS Comput Biol. 2012. PMID: 22737062 Free PMC article. - Rapid desynchronization of an electrically coupled interneuron network with sparse excitatory synaptic input.
Vervaeke K, Lorincz A, Gleeson P, Farinella M, Nusser Z, Silver RA. Vervaeke K, et al. Neuron. 2010 Aug 12;67(3):435-51. doi: 10.1016/j.neuron.2010.06.028. Neuron. 2010. PMID: 20696381 Free PMC article. - GABAA receptor-mediated tonic depolarization in developing neural circuits.
Lu JC, Hsiao YT, Chiang CW, Wang CT. Lu JC, et al. Mol Neurobiol. 2014 Apr;49(2):702-23. doi: 10.1007/s12035-013-8548-x. Epub 2013 Sep 11. Mol Neurobiol. 2014. PMID: 24022163 Review. - Slow AMPA receptors in hippocampal principal cells.
Pampaloni NP, Riva I, Carbone AL, Plested AJR. Pampaloni NP, et al. Cell Rep. 2021 Aug 3;36(5):109496. doi: 10.1016/j.celrep.2021.109496. Cell Rep. 2021. PMID: 34348150 Free PMC article.
References
- Koch C. Biophysics of computation: Information processing in single neurons. Oxford University Press; 1999. p. 552.
- Holt GR, Koch C. Shunting inhibition does not have a divisive effect on firing rates. Neural Comput. 1997;9:1001–13. - PubMed
- Chance FS, Abbott LF, Reyes AD. Gain modulation from background synaptic input. Neuron. 2002;35:773–82. - PubMed
- Anderson JS, Lampl I, Gillespie DC, Ferster D. The contribution of noise to contrast invariance of orientation tuning in cat visual cortex. Science. 2000;290:1968–72. - PubMed
- Treue S, Martinez Trujillo JC. Feature-based attention influences motion processing gain in macaque visual cortex. Nature. 1999;399:575–9. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
- 064413/WT_/Wellcome Trust/United Kingdom
- BB/F005369/1/BB_/Biotechnology and Biological Sciences Research Council/United Kingdom
- G0400598/MRC_/Medical Research Council/United Kingdom
- G0400598(71261)/MRC_/Medical Research Council/United Kingdom
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials