Application of elastic network models to proteins in the crystalline state - PubMed (original) (raw)

Application of elastic network models to proteins in the crystalline state

Demian Riccardi et al. Biophys J. 2009 Jan.

Erratum in

Abstract

Normal mode analysis using elastic network models has grown popular for probing the low-frequency collective dynamics of proteins and other biomolecular assemblies. In most previous studies, these models were validated by comparing calculated atomic fluctuations for isolated proteins with experimental temperature factors determined in the crystalline state, although there were also hints that including crystal contacts in the calculations has an impact on the comparison. In this study, a set of 83 ultra-high resolution crystal structures with experimentally determined anisotropic displacement parameters is used to evaluate several C(alpha)-based elastic network models that either ignore or treat the crystal environment in different ways; the latter include using periodic boundary conditions defined with respect to the asymmetric unit or the primitive unit cell as well as using the Born-von Kármán boundary condition that accounts for lattice vibrations. For all elastic network models, treating the crystal environment leads to better agreement with experimental anisotropic displacement parameters with the Born-von Kármán boundary condition giving the best agreement. Atomic correlations over the entire protein are clearly affected by the presence of the crystal contacts and fairly sensitive to the way that the crystal environment is treated. These observations highlight the importance of properly treating the protein system in an environment consistent with experiment when either evaluating approximate protein models or using approximate dynamic models in structural refinement application types. Finally, investigation of the scaling behaviors of the cumulative density of states and the heat capacity indicates that there are still gaps between simplified elastic models and all-atom models for proteins.

PubMed Disclaimer

Figures

Figure 1

Figure 1

Isolated Lysozyme (PDB ID: 3LZT) rendered with ANM interactions between atoms with 8 Å and 16 Å cutoffs on the top and bottom, respectively.

Figure 2

Figure 2

Crystal structure of tropomyosin (PDB ID: 2TMA) in the C_α_ representation. The top figure is rendered orthographically with the a axis pointing out of the page; the primitive cell is in large solid spheres and the 26 nearest neighbors are shown with smaller open spheres. The bottom figure is in perspective with a slightly rotated orientation, zoomed in on the central unit cell; the primitive unit cell has four asymmetric units (space group _P_21212): one is shown with solid black spheres (color online) and the other three are shown with solid gray spheres. Tropomyosin is involved in actin regulation and consists of two long, coiled _α_-helices that resemble a floppy noodle when taken alone. In contrast, the crystal structure has many intermolecular interactions, which yields a structure resembling chicken wire. This crystal structure is low-resolution and not included in the set of 83 proteins.

Figure 3

Figure 3

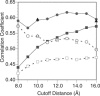
Correlation coefficient between the ANM and experimental isotropic temperature factors as a function of the ANM cutoff distance using various ways of treating the crystal environment. Each point (squares, circles, and triangles) represents a weighted average for the set of 83 proteins (Eq. 14). The solid lines and shapes include all normal modes in the calculations whereas the dashed lines and open shapes include only 5% of the modes for each protein. The squares, circles, and triangles are for the ISL, ASYMPBC, and P1PBC boundary conditions, respectively. Comparing the boundary conditions, including the crystal environment via periodic boundary conditions, clearly improves the agreement with experiment, and the largest gains are at shorter cutoff distance. Both ASYMPBC and P1PBC yield similar agreement for both set of calculations (5% and 100%). As discussed in the text, using 5% of the modes dramatically reduces the agreement, and this behavior has a strong dependence on the cutoff distance.

Figure 4

Figure 4

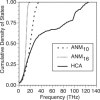
Calculated cumulative density of states for an isolated (ISL) PDZ2 domain of syntenin (PDB ID: 1R6J) using ANM10, ANM16, and HCA. For each calculation, the force constant is scaled to best fit the experimental isotropic temperature factors, which defines the range of frequencies for each model. In contrast to ANM10 and ANM16 the cumulative density of states for HCA has distinct features due to the distance-dependence of the force constant.

Figure 5

Figure 5

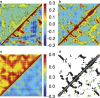
Calculated atomic correlations (Eq. 17) and contact maps for the PDZ2 domain of syntenin (PDB ID: 1R6J) using various C_α_-based ENMs and different ways of treating the crystal environment. The residue number is plotted along the x and y axes and ranges from 1 to 82 in all plots. Atomic correlations are shown in a_–_c (note the difference in scale between c and a/b): (a) ISL results obtained with ANM16 (HCA) are shown in the upper (lower) triangle. (b) ASYMPBC and P1PBC results obtained using HCA are plotted above and below the diagonal, respectively. (c) Correlations computed with BVK and 27 wavevectors using only the three acoustic modes are shown above the diagonal and results obtained with all modes below the diagonal. (d) The Kirchoff matrix for the ISL and ASYMPBC cases (using a cutoff of 10.0 Å) are plotted above and below the diagonal, respectively; blue indicates off-diagonal contacts that exist in the ISL case and green highlights contacts introduced via the crystal environment.

Similar articles

Cited by

References

    1. Corey R.B., Pauling L. Fundamental dimensions of poly-peptide chains. Proc. R. Soc. Lond. B. Biol. Sci. 1953;141:10–20. - PubMed
    1. Watson J.D., Crick F.H.C. Molecular structure of nucleic acids: a structure for deoxyribose nucleic acid. Nature. 1953;171:737–738. - PubMed
    1. Perutz M.F. Stereochemistry of cooperative effects in hemoglobin. Nature. 1970;228:726–739. - PubMed
    1. Ringe D., Petsko G.A. Study of protein dynamics by x-ray diffraction. Methods Enzymol. 1986;131:389–433. - PubMed
    1. Casper D.L.D., Clarage J., Salunke D.M., Clarage M. Liquid-like movements in crystalline insulin. Nature. 1988;332:659–662. - PubMed

Publication types

MeSH terms

Substances

LinkOut - more resources