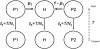Approximate bayesian computation without summary statistics: the case of admixture - PubMed (original) (raw)
Approximate bayesian computation without summary statistics: the case of admixture
Vitor C Sousa et al. Genetics. 2009 Apr.
Abstract
In recent years approximate Bayesian computation (ABC) methods have become popular in population genetics as an alternative to full-likelihood methods to make inferences under complex demographic models. Most ABC methods rely on the choice of a set of summary statistics to extract information from the data. In this article we tested the use of the full allelic distribution directly in an ABC framework. Although the ABC techniques are becoming more widely used, there is still uncertainty over how they perform in comparison with full-likelihood methods. We thus conducted a simulation study and provide a detailed examination of ABC in comparison with full likelihood in the case of a model of admixture. This model assumes that two parental populations mixed at a certain time in the past, creating a hybrid population, and that the three populations then evolve under pure drift. Several aspects of ABC methodology were investigated, such as the effect of the distance metric chosen to measure the similarity between simulated and observed data sets. Results show that in general ABC provides good approximations to the posterior distributions obtained with the full-likelihood method. This suggests that it is possible to apply ABC using allele frequencies to make inferences in cases where it is difficult to select a set of suitable summary statistics and when the complexity of the model or the size of the data set makes it computationally prohibitive to use full-likelihood methods.
Figures
Figure 1.—
The admixture model described in the text. We assume a single admixture event, T generations ago. The three populations are allowed to have different sizes _N_1, _N_2, and _N_h.
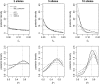
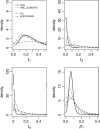
Figure 2.—
Example of posterior distributions of three runs. Results obtained for _t_h and _p_1 in three single-locus analyses, varying the number of alleles, are shown. The different lines correspond to the posteriors obtained with the different methods compared (key is shown in the top left plot). For the ABC methods the densities were obtained with the regression step. The prior distributions are shown as horizontal dotted lines and the true parameter value as dotted vertical lines.
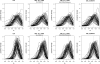
Figure 3.—
Comparison of the posterior distributions obtained for _p_1 with the different methods for the multiple biallelic loci case, with drift ti = 0.01. The results obtained with 5 and 10 loci are shown in the top and bottom rows, respectively. Each solid line corresponds to the posterior obtained for 1 of the 50 repetitions. For the ABC methods, the densities were obtained with the regression step. The prior distributions are shown as dotted horizontal lines and the true parameter values as dashed vertical lines. ABC results obtained with 108 simulations and _P_δ = 10−5.
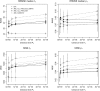
Figure 4.—
Effect of tolerance level _P_δ and regression step in the RRMSE and MISE of _p_1 and _t_h. Error values were estimated using 10 biallelic loci, with drift ti = 0.001 and _p_1 = 0.7. For the ABC methods 108 simulations were performed. Solid lines correspond to the error of the regression step and dashed lines to the error of the rejection step. LEA results are shown as a solid diamond at _P_δ = 0. Error bars of MISE correspond to the standard deviation across repetitions, and error bars for the relative RRMSE correspond to the 95%C.I., obtained with 1000 nonparametric bootstrap iterations.
Figure 5.—
Posterior distributions obtained with the different methods for the analysis of the human data set to estimate admixture in Jamaica. European and African samples were assumed to come from the parental populations _P_1 and _P_2, respectively. The ABC posteriors were based on the closest 1000 points from 10 million simulations (_P_δ = 10−4). The corresponding tolerance distances were 1.73, 1.05, and 75.00 for ABC_SUMSTAT, ABC_ALL_FREQ with _G_ST, and Euclidean, respectively. The upper limit for the drift priors was equal to one (upper limit ti = 1.0).
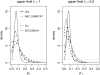
Figure 6.—
Effect of drift prior in human data set results. Posterior distributions obtained for _p_1 with the different ABC methods and LEA, varying the upper limit for ti, are shown. The ABC posteriors were based on the closest 1000 points from 10 million simulations (_P_δ = 10−4).
Similar articles
- AABC: approximate approximate Bayesian computation for inference in population-genetic models.
Buzbas EO, Rosenberg NA. Buzbas EO, et al. Theor Popul Biol. 2015 Feb;99:31-42. doi: 10.1016/j.tpb.2014.09.002. Epub 2014 Sep 26. Theor Popul Biol. 2015. PMID: 25261426 Free PMC article. - Complex genetic admixture histories reconstructed with Approximate Bayesian Computation.
Fortes-Lima CA, Laurent R, Thouzeau V, Toupance B, Verdu P. Fortes-Lima CA, et al. Mol Ecol Resour. 2021 May;21(4):1098-1117. doi: 10.1111/1755-0998.13325. Epub 2021 Feb 26. Mol Ecol Resour. 2021. PMID: 33452723 Free PMC article. - Estimating demographic parameters from large-scale population genomic data using Approximate Bayesian Computation.
Li S, Jakobsson M. Li S, et al. BMC Genet. 2012 Mar 27;13:22. doi: 10.1186/1471-2156-13-22. BMC Genet. 2012. PMID: 22453034 Free PMC article. - On the use of kernel approximate Bayesian computation to infer population history.
Nakagome S. Nakagome S. Genes Genet Syst. 2015;90(3):153-62. doi: 10.1266/ggs.90.153. Genes Genet Syst. 2015. PMID: 26510570 Review. - ABC as a flexible framework to estimate demography over space and time: some cons, many pros.
Bertorelle G, Benazzo A, Mona S. Bertorelle G, et al. Mol Ecol. 2010 Jul;19(13):2609-25. doi: 10.1111/j.1365-294X.2010.04690.x. Epub 2010 Jun 18. Mol Ecol. 2010. PMID: 20561199 Review.
Cited by
- On the structural plasticity of the human genome: chromosomal inversions revisited.
Alves JM, Lopes AM, Chikhi L, Amorim A. Alves JM, et al. Curr Genomics. 2012 Dec;13(8):623-32. doi: 10.2174/138920212803759703. Curr Genomics. 2012. PMID: 23730202 Free PMC article. - MTML-msBayes: approximate Bayesian comparative phylogeographic inference from multiple taxa and multiple loci with rate heterogeneity.
Huang W, Takebayashi N, Qi Y, Hickerson MJ. Huang W, et al. BMC Bioinformatics. 2011 Jan 3;12:1. doi: 10.1186/1471-2105-12-1. BMC Bioinformatics. 2011. PMID: 21199577 Free PMC article. - Lack of confidence in approximate Bayesian computation model choice.
Robert CP, Cornuet JM, Marin JM, Pillai NS. Robert CP, et al. Proc Natl Acad Sci U S A. 2011 Sep 13;108(37):15112-7. doi: 10.1073/pnas.1102900108. Epub 2011 Aug 29. Proc Natl Acad Sci U S A. 2011. PMID: 21876135 Free PMC article. - Evolution of lactase persistence: an example of human niche construction.
Gerbault P, Liebert A, Itan Y, Powell A, Currat M, Burger J, Swallow DM, Thomas MG. Gerbault P, et al. Philos Trans R Soc Lond B Biol Sci. 2011 Mar 27;366(1566):863-77. doi: 10.1098/rstb.2010.0268. Philos Trans R Soc Lond B Biol Sci. 2011. PMID: 21320900 Free PMC article. - Atlantic salmon populations invaded by farmed escapees: quantifying genetic introgression with a Bayesian approach and SNPs.
Glover KA, Pertoldi C, Besnier F, Wennevik V, Kent M, Skaala Ø. Glover KA, et al. BMC Genet. 2013 Aug 23;14:74. doi: 10.1186/1471-2156-14-74. BMC Genet. 2013. PMID: 23968202 Free PMC article.
References
- Beaumont, M., J. Cornuet, J. Marin and C. Robert, 2009. Adaptivity for approximate Bayesian computation algorithms: a population Monte Carlo approach. Biometrika (in press).
- Beaumont, M. A., and B. Rannala, 2004. The Bayesian revolution in genetics. Nat. Rev. Genet. 5 251–261. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Miscellaneous