Accurate detection of recombinant breakpoints in whole-genome alignments - PubMed (original) (raw)
Accurate detection of recombinant breakpoints in whole-genome alignments
Oscar Westesson et al. PLoS Comput Biol. 2009 Mar.
Abstract
We propose a novel method for detecting sites of molecular recombination in multiple alignments. Our approach is a compromise between previous extremes of computationally prohibitive but mathematically rigorous methods and imprecise heuristic methods. Using a combined algorithm for estimating tree structure and hidden Markov model parameters, our program detects changes in phylogenetic tree topology over a multiple sequence alignment. We evaluate our method on benchmark datasets from previous studies on two recombinant pathogens, Neisseria and HIV-1, as well as simulated data. We show that we are not only able to detect recombinant regions of vastly different sizes but also the location of breakpoints with great accuracy. We show that our method does well inferring recombination breakpoints while at the same time maintaining practicality for larger datasets. In all cases, we confirm the breakpoint predictions of previous studies, and in many cases we offer novel predictions.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
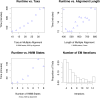
Figure 1. Accuracy of breakpoint detection varies as a function of simulation and inference parameters.
In each case, we plot both positive predictive value (TP/(TP+FP) = PPV ) and sensitivity (TP/(TP+FN)). A correctly predicted breakpoint is defined as one which occurs less than 10 bp from a true breakpoint. We observe that the overall accuracy remains high except for situations of high diversity, extremely short recombinant region (less than 50 bp), or more than 20 taxa. In several cases, we were resource-limited and only able to provide a few data points for each variable, and this is the reason for the sparseness of the plots. Each data point is the maximum-likelihood outcome of 10 independently run EM trials, each one taking on average 15 minutes for small length/taxa, though this varies as seen in Figure 9.
Figure 2. The detection power increases as more trees are added to the model.
Here we analyze alignments with 5 regions, while setting our predicted number of states to various values. The sensitivity increases steadily while PPV tapers off at a fixed value.
Figure 3. Analyses of Neisseria argF (left) and penA (right) data.
The left plot shows the analysis of Neisseria argF data with predictions from Husmeier and Wright, who used a similar method, in red dashed lines. We confirm each of their breakpoints and are able to better characterize uncertain regions. Still, the region from 0–75 remains difficult to characterize. Different colors represent posterior probabilities of different tree-topology states in the HMM, and sharp changes in color indicates likely recombination breakpoints. The right figure shows analysis of Neisseria penA data, an alignment of 9 taxa of length circa 1900 bp, demonstrating our ability to analyze many taxa. We confirm with high posterior probabilities the two breakpoints previously found by Bowler et al., shown in red .
Figure 4. The top figure shows our analysis of the strain CRF01_AE/B Malaysian HIV-1 with our recombination phylo-HMM.
We recover 6 previously predicted recombination breakpoints (red), and predict new regions in 6415–6594 and 2360–2553 (green). The grey and black regions correspond to posterior probabilities of the trees shown in the lowest figure. Previous bootscanning analysis of the same data is shown in the middle figure . Since this previous analysis involved removing gaps from the alignment, we provide approximate mappings from our predictions to theirs, as the red dashed lines between the two figures. They provided precise breakpoint locations in based on consensus HXB2 strain, which we plot in our figure as the vertical red lines. Note the spike in their plot that appears in our plot around 6500 as a recombinant region. The trees in the lowest figure were those trained as hidden states in our HMM; the black state clearly shows the query strain clustering with CRF_AE, whereas the gray tree shows a closer relationship with subtype B, in accordance with the previous findings.
Figure 5. Analysis of A/C Indian HIV-1 recombinant strain 95IN21301.
In the original paper , gaps were stripped and so mapping predictions to our plot is difficult. Instead, we show our confirmations in red, which correspond closely to the predictions seen in Figures 1 and 2 of . Our new prediction of region 4328–4401 is shown in green. Trees trained as hidden HMM states are shown underneath, with their colored boxes corresponding to the colors in the plot, which in turn denote posterior probabilities of hidden states. Note that in the black tree the query sequence doesn't cluster with C, but the branch length from the (C,F) clade to the query strain is effectively zero, indicating a star-like topology in these areas.
Figure 6. Brazilian strain BREPM12313.
We confirm Filho et al.'s breakpoints near 1322 and 2571 (red), and predict new recombinant regions in nt 4784–4945 as well as 970–1049 (green). The second of these is short, but present in some form in all three strains analyzed here. The spike at 3851–3909 is even shorter and is not represented in the other two species, leading us to not predict it as a likely recombinant region. Trees trained in hidden states are shown below the plot.
Figure 7. Brazilian strain BREPM16704.
We confirm breakpoints near 1322, 2571, and 5462 (red) and predict recombinations in 9281–9405 and 1017–1085 (green). Trees trained in hidden states are shown below the plot.
Figure 8. Brazilian strain BREPM11871.
Confirmation of breakpoints 1322 and 2571, and 4782 (red dashed lines). We predict a region common to BREPM16704 at 9238–9361 (green). Also, the breakpoint previously estimated at 5462 (red) we propose to be at 5277 (green dashed line). In support of this, we provide bootstrapping values (1000 replicates) for the 3 different regions, indicated by horizontal colored lines above the plot. Our prediction (orange) carries the highest value, 99.9%, whereas the previous (blue) is only 85.1%, since it includes a region (purple) that strongly supports BREPM11871 clustering with subtype B, with value 98.2%. The small region at 985–1080 is difficult to confidently categorize, but its high posterior probability for clustering with F and its agreement with the other two strains lead us to suspect a recombination. Trees trained in hidden states are shown below the plot.
Figure 9. Resource use of the algorithm increases with model complexity.
The algorithm converges in a reasonable number of EM steps, as seen in the lower right plot. We observed no dependence of iterations to convergence and the model complexity, and so the lower right histogram represents data concatenated from all simulation trials. The final bar in the histogram represents the proportion of trials which took 14 or more iterations to converge.
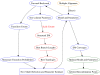
Figure 10. Phylo-HMM training algorithm.
Input Alignment ⇒ Model Selection/Parameter Estimation ⇒ Recombination Inference.
Similar articles
- Detecting recombination with MCMC.
Husmeier D, McGuire G. Husmeier D, et al. Bioinformatics. 2002;18 Suppl 1:S345-53. doi: 10.1093/bioinformatics/18.suppl_1.s345. Bioinformatics. 2002. PMID: 12169565 - GARD: a genetic algorithm for recombination detection.
Kosakovsky Pond SL, Posada D, Gravenor MB, Woelk CH, Frost SD. Kosakovsky Pond SL, et al. Bioinformatics. 2006 Dec 15;22(24):3096-8. doi: 10.1093/bioinformatics/btl474. Epub 2006 Nov 16. Bioinformatics. 2006. PMID: 17110367 - Genome resequencing and genetic variation.
Stratton M. Stratton M. Nat Biotechnol. 2008 Jan;26(1):65-6. doi: 10.1038/nbt0108-65. Nat Biotechnol. 2008. PMID: 18183021 Review. No abstract available. - Homology assessment and molecular sequence alignment.
Phillips AJ. Phillips AJ. J Biomed Inform. 2006 Feb;39(1):18-33. doi: 10.1016/j.jbi.2005.11.005. Epub 2005 Dec 9. J Biomed Inform. 2006. PMID: 16380300 Review.
Cited by
- The impact of mutation and gene conversion on the local diversification of antigen genes in African trypanosomes.
Gjini E, Haydon DT, Barry JD, Cobbold CA. Gjini E, et al. Mol Biol Evol. 2012 Nov;29(11):3321-31. doi: 10.1093/molbev/mss166. Epub 2012 Jun 25. Mol Biol Evol. 2012. PMID: 22735079 Free PMC article. - Classification of HIV-1 sequences using profile Hidden Markov Models.
Dwivedi SK, Sengupta S. Dwivedi SK, et al. PLoS One. 2012;7(5):e36566. doi: 10.1371/journal.pone.0036566. Epub 2012 May 18. PLoS One. 2012. PMID: 22623958 Free PMC article. - Detection of homologous recombination events in bacterial genomes.
Wang WB, Jiang T, Gardner S. Wang WB, et al. PLoS One. 2013 Oct 7;8(10):e75230. doi: 10.1371/journal.pone.0075230. eCollection 2013. PLoS One. 2013. PMID: 24116030 Free PMC article. - Distributed genotyping and clustering of Neisseria strains reveal continual emergence of epidemic meningococcus over a century.
Zhong L, Zhang M, Sun L, Yang Y, Wang B, Yang H, Shen Q, Xia Y, Cui J, Hang H, Ren Y, Pang B, Deng X, Zhan Y, Li H, Zhou Z. Zhong L, et al. Nat Commun. 2023 Nov 24;14(1):7706. doi: 10.1038/s41467-023-43528-0. Nat Commun. 2023. PMID: 38001084 Free PMC article. - A novel computational method identifies intra- and inter-species recombination events in Staphylococcus aureus and Streptococcus pneumoniae.
Sanguinetti L, Toti S, Reguzzi V, Bagnoli F, Donati C. Sanguinetti L, et al. PLoS Comput Biol. 2012;8(9):e1002668. doi: 10.1371/journal.pcbi.1002668. Epub 2012 Sep 6. PLoS Comput Biol. 2012. PMID: 22969418 Free PMC article.
References
- Awadalla P. The evolutionary genomics of pathogen recombination. Nat Rev Genet. 2003;4:50–60. - PubMed
- Hein J, Shierup H, Wiuf C. Gene Genealogies, Variation and Evolution. New York: Oxford University Press; 2005.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources