Automated high-dimensional flow cytometric data analysis - PubMed (original) (raw)
. 2009 May 26;106(21):8519-24.
doi: 10.1073/pnas.0903028106. Epub 2009 May 14.
Xinli Hu, Kui Wang, Elizabeth Rossin, Tsung-I Lin, Lisa M Maier, Clare Baecher-Allan, Geoffrey J McLachlan, Pablo Tamayo, David A Hafler, Philip L De Jager, Jill P Mesirov
Affiliations
- PMID: 19443687
- PMCID: PMC2682540
- DOI: 10.1073/pnas.0903028106
Automated high-dimensional flow cytometric data analysis
Saumyadipta Pyne et al. Proc Natl Acad Sci U S A. 2009.
Abstract
Flow cytometric analysis allows rapid single cell interrogation of surface and intracellular determinants by measuring fluorescence intensity of fluorophore-conjugated reagents. The availability of new platforms, allowing detection of increasing numbers of cell surface markers, has challenged the traditional technique of identifying cell populations by manual gating and resulted in a growing need for the development of automated, high-dimensional analytical methods. We present a direct multivariate finite mixture modeling approach, using skew and heavy-tailed distributions, to address the complexities of flow cytometric analysis and to deal with high-dimensional cytometric data without the need for projection or transformation. We demonstrate its ability to detect rare populations, to model robustly in the presence of outliers and skew, and to perform the critical task of matching cell populations across samples that enables downstream analysis. This advance will facilitate the application of flow cytometry to new, complex biological and clinical problems.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
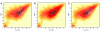
Fig. 1.
Enhanced fit using skew distribution with FLAME. (A) Expression of HLA-DQ and CD95 in a lymphoblastic cell line: A representative sample from 194 cell lines is plotted with hue intensity representing data density. The data contours, in white, show a single unimodal asymmetric population of cells. The mode estimated by skew-t modeling (cyan dot) coincides with the highest percentile contour. (B) Gaussian mixture modeling (MCLUST) yields 2 distinct subpopulations. The true (cyan dot) and estimated (center of cross) modes do not coincide. (C) FLAME fits a single skew t distribution capturing the asymmetry in 1(a) and correctly estimating the mode.
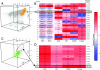
Fig. 2.
Automated discovery of a rare subset of regulatory T cells with FLAME. (A) 3-dimensional projection (for markers CD4, CD25, Foxp3) of the stained PBMCs. FLAME's 4-variate modeling yielded 19 clusters as optimal. Cluster 5 (orange) has high expression of CD4 and CD25, rendering it the best candidate to represent the regulatory T cell population. (B) Clusters' expression profiles as a heat map of the 4 markers, FSC and SSC. Lower CD4 and high FSC and SSC in cluster 2 suggest activated T cells rather than regulatory T cells. (C) Subclustering of cluster 5 yields an optimal model of 9 subpopulations. Subcluster 9 (purple) matches the CD4+DR+CD25brightFoxp3+ of regulatory T cells. Subclusters 1–8 are in green. (D) The heat map shows that subcluster 9 has the highest expression levels of DR, CD25 and Foxp3, and is 0.81% of live PBMCs, consistent with an expected frequency of ∼1%.
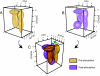
Fig. 3.
Mixture modeling of prephosphorylation and postphosphorylation T cell populations. (A and B) FLAME modeling of (A) pre- and (B) postphosphorylation data for a representative subject. The data are fit with 4-variate t mixtures projected into 3 dimensions, ZAP70 is not shown. Three-dimensional abstractions of the (A) pre- and (B) postphosphorylation clusters are shown in yellow and purple respectively. Black dots mark the cluster modes. (C) The results are superimposed, and the view is rotated to emphasize the differences in the SLP76 dimension that occur with stimulation. A green arrow indicates the increase in SLP76 phosphorylation of the naïve and memory CD4+ T cell populations and in the CD4−CD45RAintermediate population.
Similar articles
- Bayesian inference for finite mixtures of univariate and multivariate skew-normal and skew-t distributions.
Frühwirth-Schnatter S, Pyne S. Frühwirth-Schnatter S, et al. Biostatistics. 2010 Apr;11(2):317-36. doi: 10.1093/biostatistics/kxp062. Epub 2010 Jan 27. Biostatistics. 2010. PMID: 20110247 - Fluorescence-intensity multiplexing: simultaneous seven-marker, two-color immunophenotyping using flow cytometry.
Bradford JA, Buller G, Suter M, Ignatius M, Beechem JM. Bradford JA, et al. Cytometry A. 2004 Oct;61(2):142-52. doi: 10.1002/cyto.a.20037. Cytometry A. 2004. PMID: 15382027 - Modeling of inter-sample variation in flow cytometric data with the joint clustering and matching procedure.
Lee SX, McLachlan GJ, Pyne S. Lee SX, et al. Cytometry A. 2016 Jan;89(1):30-43. doi: 10.1002/cyto.a.22789. Epub 2015 Oct 22. Cytometry A. 2016. PMID: 26492316 - Analysis of protein phosphorylation and cellular signaling events by flow cytometry: techniques and clinical applications.
Krutzik PO, Irish JM, Nolan GP, Perez OD. Krutzik PO, et al. Clin Immunol. 2004 Mar;110(3):206-21. doi: 10.1016/j.clim.2003.11.009. Clin Immunol. 2004. PMID: 15047199 Review. - Intracellular cytokine detection by fluorescence-activated flow cytometry: basic principles and recent advances.
Freer G, Rindi L. Freer G, et al. Methods. 2013 May 15;61(1):30-8. doi: 10.1016/j.ymeth.2013.03.035. Epub 2013 Apr 11. Methods. 2013. PMID: 23583887 Review.
Cited by
- cytoKernel: Robust kernel embeddings for assessing differential expression of single cell data.
Ghosh T, Baxter RM, Seal S, Lui VG, Rudra P, Vu T, Hsieh EW, Ghosh D. Ghosh T, et al. bioRxiv [Preprint]. 2024 Aug 19:2024.08.16.608287. doi: 10.1101/2024.08.16.608287. bioRxiv. 2024. PMID: 39229233 Free PMC article. Preprint. - GateMeClass: Gate Mining and Classification of cytometry data.
Caligola S, Giacobazzi L, Canè S, Vella A, Adamo A, Ugel S, Giugno R, Bronte V. Caligola S, et al. Bioinformatics. 2024 May 2;40(5):btae322. doi: 10.1093/bioinformatics/btae322. Bioinformatics. 2024. PMID: 38775676 Free PMC article. - Characterization of CD34+ Cells from Patients with Acute Myeloid Leukemia (AML) and Myelodysplastic Syndromes (MDS) Using a t-Distributed Stochastic Neighbor Embedding (t-SNE) Protocol.
Nollmann C, Moskorz W, Wimmenauer C, Jäger PS, Cadeddu RP, Timm J, Heinzel T, Haas R. Nollmann C, et al. Cancers (Basel). 2024 Mar 28;16(7):1320. doi: 10.3390/cancers16071320. Cancers (Basel). 2024. PMID: 38610998 Free PMC article. - A cell-level discriminative neural network model for diagnosis of blood cancers.
Robles EE, Jin Y, Smyth P, Scheuermann RH, Bui JD, Wang HY, Oak J, Qian Y. Robles EE, et al. Bioinformatics. 2023 Oct 3;39(10):btad585. doi: 10.1093/bioinformatics/btad585. Bioinformatics. 2023. PMID: 37756695 Free PMC article. - Statistical and machine learning methods for immunoprofiling based on single-cell data.
Zhang J, Li J, Lin L. Zhang J, et al. Hum Vaccin Immunother. 2023 Aug 1;19(2):2234792. doi: 10.1080/21645515.2023.2234792. Epub 2023 Jul 24. Hum Vaccin Immunother. 2023. PMID: 37485833 Free PMC article. Review.
References
- Perfetto SP, Chattopadhyay PK, Roederer M. Seventeen-colour flow cytometry: Unravelling the immune system. Nat Rev. 2004;4:648–655. - PubMed
- De Rosa SC, Brenchley JM, Roederer M. Beyond six colors: A new era in flow cytometry. Nat Med. 2003;9:112–117. - PubMed
- De Rosa SC, Herzenberg LA, Herzenberg LA, Roederer M. 11-color, 13-parameter flow cytometry: Identification of human naive T cells by phenotype, function, and T-cell receptor diversity. Nat Med. 2001;7:245–248. - PubMed
- Irish JM, Kotecha N, Nolan GP. Mapping normal and cancer cell signalling networks: Towards single-cell proteomics. Nat Rev. 2006;6:146–155. - PubMed
- Lo K, Brinkman RR, Gottardo R. Automated gating of flow cytometry data via robust model-based clustering. Cytometry A. 2008;73:321–332. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources