Permeability calculations in three-dimensional isotropic and oriented fiber networks - PubMed (original) (raw)
Permeability calculations in three-dimensional isotropic and oriented fiber networks
Triantafyllos Stylianopoulos et al. Phys Fluids (1994). 2008 Dec.
Abstract
Hydraulic permeabilities of fiber networks are of interest for many applications and have been studied extensively. There is little work, however, on permeability calculations in three-dimensional random networks. Computational power is now sufficient to calculate permeabilities directly by constructing artificial fiber networks and simulating flow through them. Even with today's high-performance computers, however, such an approach would be infeasible for large simulations. It is therefore necessary to develop a correlation based on fiber volume fraction, radius, and orientation, preferably by incorporating previous studies on isotropic or structured networks. In this work, the direct calculations were performed, using the finite element method, on networks with varying degrees of orientation, and combinations of results for flows parallel and perpendicular to a single fiber or an array thereof, using a volume-averaging theory, were compared to the detailed analysis. The detailed model agreed well with existing analytical solutions for square arrays of fibers up to fiber volume fractions of 46% for parallel flow and 33% for transverse flow. Permeability calculations were then performed for isotropic and oriented fiber networks within the fiber volume fraction range of 0.3%-15%. When drag coefficients for spatially periodic arrays were used, the results of the volume-averaging method agreed well with the direct finite element calculations. On the contrary, the use of drag coefficients for isolated fibers overpredicted the permeability for the volume fraction range that was employed. We concluded that a weighted combination of drag coefficients for spatially periodic arrays of fibers could be used as a good approximation for fiber networks, which further implies that the effect of the fiber volume fraction and orientation on the permeability of fiber networks are more important than the effect of local network structure.
Figures
Figure 1
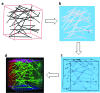
The four steps for the generation of the FE mesh from the fiber networks. (a) The initial network generated with the method described in Sec. 2A. (b) The parasolid model of the fibers. (c) The parasolid model of the surrounding fluid. (d) The final FE mesh.
Figure 2
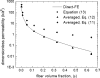
Permeability calculations for parallel flow in a square array of fibers.
Figure 3
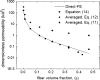
Permeability calculations for transverse flow in a square array of fibers.
Figure 4
The isotropic 4 (left), the moderately aligned 4 (center), and the highly aligned 4 (right) networks that were employed in the calculations. Structural properties of these networks are shown in Table 1.
Figure 5
The streamlines for flow through the isotropic fiber network 4.
Figure 6
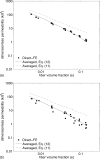
Permeability calculations for isotropic fiber networks. The permeability calculated using Eqs. 11, 12 is the average over the five isotropic networks.
Figure 7
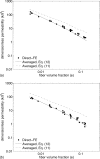
(a) Permeability calculations for flow parallel to the preferred fiber direction of the moderately oriented networks. (b) Permeability calculations for flow transverse to the preferred fiber direction of the moderately oriented networks. The permeability calculated using Eqs. 11, 12 is the average over the five moderately aligned networks.
Figure 8
(a) Permeability calculations for flow parallel to the preferred fiber direction of the strongly oriented networks. The permeability calculated using Eqs. 11, 12 is the average over the five highly aligned networks. (b) Permeability calculations for flow transverse to the preferred fiber direction of the strongly oriented networks. The permeability calculated using Eqs. 11, 12 is the average over the five highly aligned networks.
Figure 9
Dependence of the permeability on the network orientation. (◼) Isotropic networks, (△) moderately aligned networks (parallel flow), (▽) moderately aligned networks (transverse flow), (×) highly aligned networks (parallel flow), and (*) highly aligned networks (transverse flow).
Figure 10
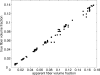
True vs apparent fiber volume fraction for the networks used in this study.
Similar articles
- Computational modeling for prediction of the shear stress of three-dimensional isotropic and aligned fiber networks.
Park S. Park S. Comput Methods Programs Biomed. 2017 Sep;148:91-98. doi: 10.1016/j.cmpb.2017.06.019. Epub 2017 Jun 29. Comput Methods Programs Biomed. 2017. PMID: 28774442 - Orthotropic hydraulic permeability of arrays of parallel cylinders.
Maleki M, Martinuzzi RJ, Herzog W, Federico S. Maleki M, et al. Phys Rev E. 2017 Sep;96(3-1):033112. doi: 10.1103/PhysRevE.96.033112. Epub 2017 Sep 25. Phys Rev E. 2017. PMID: 29346921 - Numerical analysis of viscous flow through fibrous media: a model for glomerular basement membrane permeability.
Palassini M, Remuzzi A. Palassini M, et al. Am J Physiol. 1998 Jan;274(1):F223-31. doi: 10.1152/ajprenal.1998.274.1.F223. Am J Physiol. 1998. PMID: 9458843 - Effect of micropolar fluid properties on the hydraulic permeability of fibrous biomaterials.
Karvelas EG, Tsiantis A, Papathanasiou TD. Karvelas EG, et al. Comput Methods Programs Biomed. 2020 Mar;185:105135. doi: 10.1016/j.cmpb.2019.105135. Epub 2019 Oct 16. Comput Methods Programs Biomed. 2020. PMID: 31671342 - Numerical modeling of anisotropic fiber bundle behavior in oxygenators.
Bhavsar SS, Schmitz-Rode T, Steinseifer U. Bhavsar SS, et al. Artif Organs. 2011 Nov;35(11):1095-102. doi: 10.1111/j.1525-1594.2011.01365.x. Epub 2011 Oct 5. Artif Organs. 2011. PMID: 21973082
Cited by
- Strong triaxial coupling and anomalous Poisson effect in collagen networks.
Ban E, Wang H, Franklin JM, Liphardt JT, Janmey PA, Shenoy VB. Ban E, et al. Proc Natl Acad Sci U S A. 2019 Apr 2;116(14):6790-6799. doi: 10.1073/pnas.1815659116. Epub 2019 Mar 20. Proc Natl Acad Sci U S A. 2019. PMID: 30894480 Free PMC article. - The hydraulic permeability of blood clots as a function of fibrin and platelet density.
Wufsus AR, Macera NE, Neeves KB. Wufsus AR, et al. Biophys J. 2013 Apr 16;104(8):1812-23. doi: 10.1016/j.bpj.2013.02.055. Biophys J. 2013. PMID: 23601328 Free PMC article. - Modulating the Tumor Microenvironment to Enhance Tumor Nanomedicine Delivery.
Zhang B, Hu Y, Pang Z. Zhang B, et al. Front Pharmacol. 2017 Dec 22;8:952. doi: 10.3389/fphar.2017.00952. eCollection 2017. Front Pharmacol. 2017. PMID: 29311946 Free PMC article. Review. - A Study on the Through-Plane Permeability of Anisotropic Fibrous Porous Material by Fractal Stochastic Method.
Xu Y, Xu L, Qiu S, Jiang Z, Rao B, Xu P. Xu Y, et al. Materials (Basel). 2022 Nov 15;15(22):8064. doi: 10.3390/ma15228064. Materials (Basel). 2022. PMID: 36431552 Free PMC article. - Multiscale biphasic modelling of peritumoural collagen microstructure: The effect of tumour growth on permeability and fluid flow.
Wijeratne PA, Hipwell JH, Hawkes DJ, Stylianopoulos T, Vavourakis V. Wijeratne PA, et al. PLoS One. 2017 Sep 13;12(9):e0184511. doi: 10.1371/journal.pone.0184511. eCollection 2017. PLoS One. 2017. PMID: 28902902 Free PMC article.
References
- Ghassemzadeh J. and Sahimi M., “Pore network simulation of fluid imbibition into paper during coating: II. Characterization of paper’s morphology and computation of its effective permeability tensor,” Chem. Eng. Sci. CESCAC10.1016/j.ces.2004.01.057 59, 2265 (2004). - DOI
- Koponen A., Kandhai D., Hellen E., Alava M., Hoekstra A., Kataja M., Niskanen K., Sloot P., and Timonen J., “Permeability of three-dimensional random fiber webs,” Phys. Rev. Lett. PRLTAO10.1103/PhysRevLett.80.716 80, 716 (1998). - DOI
- Schweers E. and Loffler F., “Realistic modeling of the behaviour of fibrous filters through consideration of filter structure,” Powder Technol. POTEBX10.1016/0032-5910(94)02850-8 80, 191 (1994). - DOI
- Skartsis L., Kardos J. L., and Khomami B., “Resin flow through fiber beds during composite manufacturing processes. Part I: Review of Newtonian flow through fiber beds,” Polym. Eng. Sci. PYESAZ10.1002/pen.760320402 32, 221 (1992). - DOI
LinkOut - more resources
Full Text Sources