A toolbox for the fast information analysis of multiple-site LFP, EEG and spike train recordings - PubMed (original) (raw)
A toolbox for the fast information analysis of multiple-site LFP, EEG and spike train recordings
Cesare Magri et al. BMC Neurosci. 2009.
Abstract
Background: Information theory is an increasingly popular framework for studying how the brain encodes sensory information. Despite its widespread use for the analysis of spike trains of single neurons and of small neural populations, its application to the analysis of other types of neurophysiological signals (EEGs, LFPs, BOLD) has remained relatively limited so far. This is due to the limited-sampling bias which affects calculation of information, to the complexity of the techniques to eliminate the bias, and to the lack of publicly available fast routines for the information analysis of multi-dimensional responses.
Results: Here we introduce a new C- and Matlab-based information theoretic toolbox, specifically developed for neuroscience data. This toolbox implements a novel computationally-optimized algorithm for estimating many of the main information theoretic quantities and bias correction techniques used in neuroscience applications. We illustrate and test the toolbox in several ways. First, we verify that these algorithms provide accurate and unbiased estimates of the information carried by analog brain signals (i.e. LFPs, EEGs, or BOLD) even when using limited amounts of experimental data. This test is important since existing algorithms were so far tested primarily on spike trains. Second, we apply the toolbox to the analysis of EEGs recorded from a subject watching natural movies, and we characterize the electrodes locations, frequencies and signal features carrying the most visual information. Third, we explain how the toolbox can be used to break down the information carried by different features of the neural signal into distinct components reflecting different ways in which correlations between parts of the neural signal contribute to coding. We illustrate this breakdown by analyzing LFPs recorded from primary visual cortex during presentation of naturalistic movies.
Conclusion: The new toolbox presented here implements fast and data-robust computations of the most relevant quantities used in information theoretic analysis of neural data. The toolbox can be easily used within Matlab, the environment used by most neuroscience laboratories for the acquisition, preprocessing and plotting of neural data. It can therefore significantly enlarge the domain of application of information theory to neuroscience, and lead to new discoveries about the neural code.
Figures
Figure 1
Components of the information breakdown. This figure shows a schematic representation of the terms of the information breakdown of Ref. [17]. The information breakdown takes the joint mutual information I(S; R) and breaks it down into the sum of two terms: I lin (the sum of information carried by each element of the response array) and syn (the amount of synergistic information). The synergy can be further broken down into the terms I _sig_-sim and I cor which highlight the effect of different modes of correlation. I _sig_-sim quantifies the impact of signal correlations on the total information, while I cor quantifies the effect of noise correlation. The term I cor is finally broken down into I _cor_-ind and I _cor_-dep, which describe the effects of stimulus-independent and stimulus-dependent correlations respectively.
Figure 2
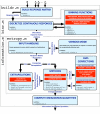
Structure of the main routines in the ToolBox. The core function is
entropy.m
which allows to compute the entropy-like quantities which constitute the building blocks for the calculation of mutual information and of all the other breakdown terms. It is important to note how the modular structure allows for new methods and extrapolation procedures to be easily created and linked to the existing software. In particular, starting with the next release of the toolbox, users will be given the opportunity to easily plug-in their custom bias correction m-files in order to extend the capabilities of the existing code. Other routines in the toolbox are available for the pre-processing of the input to
entropy.m. buildr.m
allows to build the response-matrix to be fed to the information routines starting from L + 1  -long arrays: the first array stores a list specifying, for each trial, which stimulus was presented to the subject while the L remaining arrays specify the L corresponding recorded responses.
-long arrays: the first array stores a list specifying, for each trial, which stimulus was presented to the subject while the L remaining arrays specify the L corresponding recorded responses.
binr.m
allows to discretize continuous response-matrices – prior to calls to
entropy.m
with the the Direct Method – according to a binning method chosen among a list of available binning options. Again, users are given the possibility to define their own binning strategy (in addition to the built-in binning methods) and to easily link their code to the toolbox. Finally,
information.m
is a wrapper around
entropy.m
which directly computes the breakdown terms by combining the outputs from this main function, thus skipping all the complex computations necessary for the the calculation of the breakdown quantities.
Figure 3
Comparison of the sampling properties of different information quantities and of bias correction techniques. The estimates of information and entropies obtained with a number of techniques are tested on simulated data and plotted as a function of the number of generated trials per stimulus. Results were averaged over a number of repetitions of the simulation (mean value ± st. dev. over 50 simulations). We generated simulated LFPs which matched the second order statistics of LFPs recorded from primary visual cortex during visual stimulation with color movies (see Appendix A). The neural response r used to compute information was a two dimensional response array r = [_r_1, _r_2] containing the simulated LFP power at frequencies _f_1 = 4 Hz and _f_2 = 75 Hz, respectively. The power at each frequency was binned into 6 equi-populated values. A: Values of the four plug-in entropies H(R), H(R|S), H ind(R|S) and H sh(R|S). B: Values of the bootstrap estimates of the quantities in Panel (A), computed by randomly pairing trials and stimuli. C: Mutual information values obtained with plug-in estimate (black line) and following the application of two bias correction procedures, namely QE (red line) and PT (green line). D: values of the same quantities reported in panel (C), but after further subtracting the bootstrap correction. E: Values of the information I sh(S; R) computed using the shuffling procedure with the following bias corrections: plug-in (black line); QE (red line) and PT (green line). F: values of the same quantities reported in panel (E), but after further subtracting the bootstrap correction.
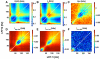
Figure 4
The information conveyed jointly by V1 LFPs at pairs of frequencies and its breakdown in terms of different correlational components. The breakdown of the information about naturalistic color movies carried by the power of LFPs at two different frequencies _f_1 and _f_2. Results are plotted as function of _f_1 and _f_2, and averaged over a set of 51 recording sites obtained from primary visual cortex of anaesthetized macaques. All estimates were computed using the Direct Method corrected with the QE bias correction procedure and the bootstrap subtraction. Each analog LFP power response was binned into 6 equi-populated values. A: The information, I(S;  ,
,  ), conveyed jointly about the stimulus by pairs of LFP power responses B: The linear sum, I lin(S;
), conveyed jointly about the stimulus by pairs of LFP power responses B: The linear sum, I lin(S;  ,
,  ), of the information conveyed independently by each response. C: The synergy syn(
), of the information conveyed independently by each response. C: The synergy syn( ,
,  ), between the responses at the two frequencies. D: The signal-similarity term I _sig_-sim E: The stimulus-independent noise correlation component I _cor_-ind F: the stimulus-dependent correlational component I _cor_-dep.
), between the responses at the two frequencies. D: The signal-similarity term I _sig_-sim E: The stimulus-independent noise correlation component I _cor_-ind F: the stimulus-dependent correlational component I _cor_-dep.
Figure 5
A comparison of Gaussian and Direct information estimation on V1 LFPs. A: This panel compares the values of information about naturalistic movies carried by V1 LFPs with the Gaussian and the Direct methods. It shows a scatter plot of the information conveyed about the movie by a single LFP frequency computed either with the Gaussian Method, or as a Direct estimate with data discretized into 8 bins. Data were taken from channel 7 of session D04 of the dataset reported in Ref. [29]. Each dot represents an information value obtained at a different LFP frequency with the two techniques considered. This figure shows that, on this dataset, the Gaussian and the Direct calculations provide similar values. The Pearson correlation coefficient between the values computed with the two methods was 0.99. B: We tested the Gaussian estimates of information on simulated data. We generated simulated LFPs which matched the second order statistics of LFPs recorded from primary visual cortex during visual stimulation with color movies (see Appendix A). The neural response r used to compute information was either a one, a two or a three dimensional response array containing the simulated LFP power at frequencies of 4, 25 and 75 Hz. The estimates of the mutual information carried by the power at either one, two or three frequencies were computed using these data and the Gaussian Method and was plotted as function of the generated number of trials per stimulus (mean value ± the standard deviation over 50 simulations). Solid lines and dotted lines represent Gaussian estimates obtained without and with the subtraction of the analytic gaussian bias correction (see text) respectively.
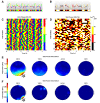
Figure 6
Information analysis of EEG recordings during vision of naturalistic movies. The Figure shows EEG responses, and their information, recorded from a human subject watching 5 s-long repeated presentations of a color movie. Data from Panels (A-D) were taken from an example electrode (whose location is reported by the arrow in Panels E-F). A: The time course of the phase of the delta-band (0.1 – 4 Hz) EEG during a single trial (i.e., a single movie presentation). The single-trial delta-band EEG has been color-coded according to its phase-angle binned into four equally spaced intervals between -π and π. B: The same single-trial delta-band EEG from the example electrode was color-coded according to the instantaneous power binned into four equally probable intervals. C: Time course of the instantaneous phases of the 0.1 – 4 Hz (delta) EEG from the example electrode over 30 repetitions of the movie. Phase values were color coded into quadrants exactly as illustrated in Panel (A). D: Time course of the binned instantaneous power of the 0.1 – 4 Hz (delta) EEG from the example electrode over 30 repetitions of the movie. Power values were color coded into quadrants exactly as illustrated in Panel (B). E: The information conveyed by the binned phase in the delta (0 – 4 Hz), theta (4 – 8 Hz), alpha (8 – 15 Hz) and beta (15 – 30 Hz) frequency bands is plotted topographically across the electrode locations. F: The same topographic plot for the EEG instantaneous power information.
Similar articles
- Cortical dynamics during naturalistic sensory stimulations: experiments and models.
Mazzoni A, Brunel N, Cavallari S, Logothetis NK, Panzeri S. Mazzoni A, et al. J Physiol Paris. 2011 Jan-Jun;105(1-3):2-15. doi: 10.1016/j.jphysparis.2011.07.014. Epub 2011 Aug 31. J Physiol Paris. 2011. PMID: 21907800 - Unbiased and robust quantification of synchronization between spikes and local field potential.
Li Z, Cui D, Li X. Li Z, et al. J Neurosci Methods. 2016 Aug 30;269:33-8. doi: 10.1016/j.jneumeth.2016.05.004. Epub 2016 May 13. J Neurosci Methods. 2016. PMID: 27180930 - Spike train analysis toolkit: enabling wider application of information-theoretic techniques to neurophysiology.
Goldberg DH, Victor JD, Gardner EP, Gardner D. Goldberg DH, et al. Neuroinformatics. 2009 Sep;7(3):165-78. doi: 10.1007/s12021-009-9049-y. Epub 2009 May 28. Neuroinformatics. 2009. PMID: 19475519 Free PMC article. - Information-theoretic methods for studying population codes.
Ince RA, Senatore R, Arabzadeh E, Montani F, Diamond ME, Panzeri S. Ince RA, et al. Neural Netw. 2010 Aug;23(6):713-27. doi: 10.1016/j.neunet.2010.05.008. Epub 2010 Jun 12. Neural Netw. 2010. PMID: 20542408 Review. - In Vivo Observations of Rapid Scattered Light Changes Associated with Neurophysiological Activity.
Rector DM, Yao X, Harper RM, George JS. Rector DM, et al. In: Frostig RD, editor. In Vivo Optical Imaging of Brain Function. 2nd edition. Boca Raton (FL): CRC Press/Taylor & Francis; 2009. Chapter 5. In: Frostig RD, editor. In Vivo Optical Imaging of Brain Function. 2nd edition. Boca Raton (FL): CRC Press/Taylor & Francis; 2009. Chapter 5. PMID: 26844322 Free Books & Documents. Review.
Cited by
- Theta-gamma phase-amplitude coupling in auditory cortex is modulated by language proficiency.
Lizarazu M, Carreiras M, Molinaro N. Lizarazu M, et al. Hum Brain Mapp. 2023 May;44(7):2862-2872. doi: 10.1002/hbm.26250. Epub 2023 Feb 27. Hum Brain Mapp. 2023. PMID: 36852454 Free PMC article. - A Tutorial for Information Theory in Neuroscience.
Timme NM, Lapish C. Timme NM, et al. eNeuro. 2018 Sep 11;5(3):ENEURO.0052-18.2018. doi: 10.1523/ENEURO.0052-18.2018. eCollection 2018 May-Jun. eNeuro. 2018. PMID: 30211307 Free PMC article. Review. - EEG Functional Connectivity is a Weak Predictor of Causal Brain Interactions.
Vink JJT, Klooster DCW, Ozdemir RA, Westover MB, Pascual-Leone A, Shafi MM. Vink JJT, et al. Brain Topogr. 2020 Mar;33(2):221-237. doi: 10.1007/s10548-020-00757-6. Epub 2020 Feb 24. Brain Topogr. 2020. PMID: 32090281 Free PMC article. - Deciphering the functional role of spatial and temporal muscle synergies in whole-body movements.
Delis I, Hilt PM, Pozzo T, Panzeri S, Berret B. Delis I, et al. Sci Rep. 2018 May 30;8(1):8391. doi: 10.1038/s41598-018-26780-z. Sci Rep. 2018. PMID: 29849101 Free PMC article. - Estimating Neuronal Information: Logarithmic Binning of Neuronal Inter-Spike Intervals.
Dorval AD. Dorval AD. Entropy (Basel). 2011 Feb 1;13(2):485-501. doi: 10.3390/e13020485. Entropy (Basel). 2011. PMID: 24839390 Free PMC article.
References
- Shannon C. A mathematical theory of communcation. Bell Systems Technical Journal. 1948;27:379–423.
- Cover TM, Thomas JA. Elements of information theory. New York: John Wiley; 2006.
- Rieke F, Warland D, van Steveninck R, Bialek W. Spikes: exploring the neural code. Cambridge: MIT Press; 1997.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources