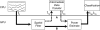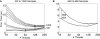Massively Parallel Signal Processing using the Graphics Processing Unit for Real-Time Brain-Computer Interface Feature Extraction - PubMed (original) (raw)

Massively Parallel Signal Processing using the Graphics Processing Unit for Real-Time Brain-Computer Interface Feature Extraction

J Adam Wilson et al. Front Neuroeng. 2009.

Abstract

The clock speeds of modern computer processors have nearly plateaued in the past 5 years. Consequently, neural prosthetic systems that rely on processing large quantities of data in a short period of time face a bottleneck, in that it may not be possible to process all of the data recorded from an electrode array with high channel counts and bandwidth, such as electrocorticographic grids or other implantable systems. Therefore, in this study a method of using the processing capabilities of a graphics card [graphics processing unit (GPU)] was developed for real-time neural signal processing of a brain-computer interface (BCI). The NVIDIA CUDA system was used to offload processing to the GPU, which is capable of running many operations in parallel, potentially greatly increasing the speed of existing algorithms. The BCI system records many channels of data, which are processed and translated into a control signal, such as the movement of a computer cursor. This signal processing chain involves computing a matrix-matrix multiplication (i.e., a spatial filter), followed by calculating the power spectral density on every channel using an auto-regressive method, and finally classifying appropriate features for control. In this study, the first two computationally intensive steps were implemented on the GPU, and the speed was compared to both the current implementation and a central processing unit-based implementation that uses multi-threading. Significant performance gains were obtained with GPU processing: the current implementation processed 1000 channels of 250 ms in 933 ms, while the new GPU method took only 27 ms, an improvement of nearly 35 times.

Keywords: BCI2000; CUDA; NVIDIA; brain–computer interface; parallel processing.

PubMed Disclaimer

Figures

Figure 1

Figure 1

The signal processing flow in any brain–computer interface. Data recorded from the brain is processed in two general steps, comprised of feature extraction, which converts relevant brain features into an appropriate task-specific representation (e.g., frequency domain or time-domain average), and translation, which converts the brain features into a control signal. This paper focuses on the feature extraction portion, which is the most computationally extensive.

Figure 2

Figure 2

The organization of threads and memory hierarchy. Individual threads are organized into blocks, which are organized into a grid. Within a block, an individual thread has a unique three-component index which identifies its position in the block; similarly each block has a three-component index identifying its position in the grid. Each thread has a private local memory accessible only to that thread; every block has shared memory accessible to all threads in that block; and all threads can access global memory.

Figure 3

Figure 3

Threaded matrix multiplication. In this load-balanced example, four threads each calculate four samples, for a total of 16 output samples. The samples that thread 0 calculates are highlighted in gray.

Figure 4

Figure 4

Two possible data transfer paths. (A) Following the spatial filter, data is transferred to the CPU before being transferred back to the GPU for the power estimate. This incurs an additional overhead that can contribute significantly to the overall processing time. (B) The data remains on the video card after spatial filtering for the power estimation routine.

Figure 5

Figure 5

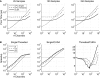
(A) The processing times for the single-threaded (dotted line), multi-threaded (dashed line), and GPU (solid line) matrix multiplication algorithms for time-series data with lengths of 25, 120, and 240 samples, which are equivalent to 50 ms of data at 512, 2400, and 4800 Hz, respectively. (B) The ratios of matrix-multiplication processing times for single-threaded to multi-threaded, single-threaded to CUDA, and multi-threaded to CUDA implementations. The results for input matrices with 25 (dotted line), 120 (dashed line), and 240 (solid line) samples are shown. A value exceeding 1 indicates that the processing time for the first implementation in the ratio exceeds that of the second implementation (e.g., if Single/Threaded >1, then the threaded version is faster). The spatial filter is a square matrix with the number of rows and columns each equal to the number of channels.

Figure 6

Figure 6

(A) The processing times for the single-threaded (dotted line), the multi-threaded (dashed line), and CUDA (solid line) auto-regressive power estimation algorithms for time-series data with lengths of 128, 600, and 1200 samples. For 1200 samples, the threaded processing time is 56 ms, while the CUDA processing time is 24.21 ms, as shown in the blow-up graph. (B) The ratios of power estimation processing times for single-threaded and multi-threaded, single-threaded and CUDA, and multi-threaded and CUDA implementations. The results for input matrices with 128 (dotted line), 600 (dashed line), and 1200 (solid line) samples are shown. A value exceeding 1 indicates that the processing time for the first implementation in the ratio exceeds that of the second implementation (e.g., if Single/Threaded >1, then the threaded version is faster).

Figure 7

Figure 7

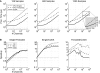
(A) Processing time using different numbers of threads with CUDA for different data lengths from 100 to 1200, in 100-sample increments, and 128 input channels. A * indicates a minimum processing time. For shorter data segments (e.g., 100–400 samples), a lower number of threads is more efficient, while for longer data segments (e.g., > 500 samples), an increased number of threads results in a faster processing time. Up to 256 threads were tested, but in no cases was 256 threads the most efficient, showing that more threads does not necessarily guarantee better performance. (B) When increasing from 654 to 656 processed samples, there is a large jump in the processing time, resulting from the way in which the data is loaded into memory on the GPU.

Figure 8

Figure 8

(A) The combined spatial filtering and power estimation processing times for single-threaded, threaded, and CUDA based implementations. The spatial filter processed one-fifth of the samples shown (i.e., 25, 120, and 240 samples), while the AR algorithm estimated the power for the total length of data. The solid horizontal line is at 50 ms, indicating the real-time performance threshold. (B) The ratios of combined spatial filtering and power estimation processing times for single-threaded and threaded, single-threaded and CUDA, and threaded and CUDA implementations. A value exceeding 1 indicates that the processing time for the first implementation in the ratio exceeds that of the second implementation (e.g., if Single/Threaded >1, then the threaded version is faster).

Figure 9

Figure 9

Comparison of processing times in μ_s_ for combined spatial filter and AR power estimates done with data transfer to and from the video card in between processing steps (CUDA + Mem), and without data transfer. The overall speedup by removing the intermediate data transfer is shown on the _Y_-axis, and is generally 1.5 to 2 times faster. The graphs show the processing times for data lengths of 125, 600, and 1200 samples, from left to right.

Similar articles

Cited by

References

    1. Andersen N. (1978). Comments on the performance of maximum entropy algorithms. Proc. IEEE 66, 1581–158210.1109/PROC.1978.11160 - DOI
    1. Burg J. P. (1975). Maximum Entropy Spectral Analysis. Ph.D. thesis, Stanford University, Stanford, CA
    1. Chen C. (1988). Signal Processing Handbook. Boca Raton, FL, CRC Press
    1. Chen T.-C., Liu W., Chen L.-G. (2008). Vlsi architecture of leading eigenvector generation for on-chip principal component analysis spike sorting system. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2008, 3192–3195 - PubMed
    1. Colicos M., Syed N. (2006). Neuronal networks and synaptic plasticity: understanding complex system dynamics by interfacing neurons with silicon technologies. J. Exp. Biol. 209, 2312–231910.1242/jeb.02163 - DOI - PubMed

LinkOut - more resources