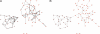Inferring friendship network structure by using mobile phone data - PubMed (original) (raw)
Inferring friendship network structure by using mobile phone data
Nathan Eagle et al. Proc Natl Acad Sci U S A. 2009.
Abstract
Data collected from mobile phones have the potential to provide insight into the relational dynamics of individuals. This paper compares observational data from mobile phones with standard self-report survey data. We find that the information from these two data sources is overlapping but distinct. For example, self-reports of physical proximity deviate from mobile phone records depending on the recency and salience of the interactions. We also demonstrate that it is possible to accurately infer 95% of friendships based on the observational data alone, where friend dyads demonstrate distinctive temporal and spatial patterns in their physical proximity and calling patterns. These behavioral patterns, in turn, allow the prediction of individual-level outcomes such as job satisfaction.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
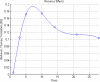
Fig. 1.
The effect of recency on self-report data. When subjects were asked to report their general proximity patterns, the survey responses were biased in favor of recent behavior. Although the correlation is lowest when only using observed behavior during the day before the survey, as we expand the observational time window to seven days, the correlation between the self-report and observed behavior increases. However, expanding the time window beyond seven days results in a decreasing correlation, leading us to conclude that subjects recall of information about their interactions begins to degrade after approximately one week.
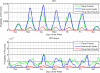
Fig. 2.
Probability of proximity. Proximity probabilities at work and off campus for symmetric friend, asymmetric friend, and nonfriend dyads. Probability of proximity is calculated for each hour in the week and is generally much higher for friends than nonfriends. However, it is also apparent that asymmetric and symmetric friend dyads have different temporal and spatial patterns in proximity, with symmetric friends spending more time together off campus in the evenings.
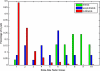
Fig. 3.
Normalized extra-role histograms. The distributions of a pair of colleagues extra-role communication factor scores segmented by relationship. Ninety-five percent (21/22) of the symmetric friendships have extra-role scores above 5, whereas ninety-six percent (901/935) of symmetric nonfriends have extra-role scores below 5. The 28 asymmetric friends have more behavioral variance, drawing from behaviors characteristic of both nonfriends and friends.
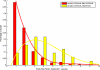
Fig. 4.
A histogram of the extra-role distribution generated from behavioral data collected from September to January for two sets of dyads. The red bins represent the dyads that consistently confirmed they were not friends on both the January and May survey (n = 2153). The yellow bins represent the dyads that confirmed they were not friends on the January survey, but at least one individual named the other as a friend on the May survey (n = 32). Clearly these two sets of dyads come from distinct distributions; potential explanations for the yellow distribution could be survey error in January (i.e., the friendships existed, but were not reported in January), or that the dyads' behavior during the autumn was indicative of budding friendships that they only became aware of during the subsequent year.
Fig. 5.
Inferred, weighted friendship network vs. reported, discrete friendship network. Frame A shows the inferred friendship network with edge weights corresponding to the factor scores for factor 2, extra-role communication. Frame B shows the reported friendship network. Node colors highlight the two groups of colleagues, first-year business school students (brown) and individuals working together in the same building (red).
Comment in
- What is a social tie?
Wuchty S. Wuchty S. Proc Natl Acad Sci U S A. 2009 Sep 8;106(36):15099-100. doi: 10.1073/pnas.0907905106. Epub 2009 Sep 1. Proc Natl Acad Sci U S A. 2009. PMID: 19805245 Free PMC article. No abstract available. - Distant friends, close strangers? Inferring friendships from behavior.
Adams J. Adams J. Proc Natl Acad Sci U S A. 2010 Mar 2;107(9):E29-30; author reply E31. doi: 10.1073/pnas.0911195107. Proc Natl Acad Sci U S A. 2010. PMID: 20197437 Free PMC article. No abstract available.
Similar articles
- A Systematic Review of Mobile Phone Data in Crime Applications: A Coherent Taxonomy Based on Data Types and Analysis Perspectives, Challenges, and Future Research Directions.
Okmi M, Por LY, Ang TF, Al-Hussein W, Ku CS. Okmi M, et al. Sensors (Basel). 2023 Apr 28;23(9):4350. doi: 10.3390/s23094350. Sensors (Basel). 2023. PMID: 37177554 Free PMC article. Review. - Calling patterns in human communication dynamics.
Jiang ZQ, Xie WJ, Li MX, Podobnik B, Zhou WX, Stanley HE. Jiang ZQ, et al. Proc Natl Acad Sci U S A. 2013 Jan 29;110(5):1600-5. doi: 10.1073/pnas.1220433110. Epub 2013 Jan 14. Proc Natl Acad Sci U S A. 2013. PMID: 23319645 Free PMC article. - A comparative analysis of the statistical properties of large mobile phone calling networks.
Li MX, Jiang ZQ, Xie WJ, Miccichè S, Tumminello M, Zhou WX, Mantegna RN. Li MX, et al. Sci Rep. 2014 May 30;4:5132. doi: 10.1038/srep05132. Sci Rep. 2014. PMID: 24875444 Free PMC article. - Survey of ownership and use of mobile phones among medical science students in Yazd.
Mazloomy Mahmoodabad SS, Barkhordari A, Nadrian H, Moshiri O, Yavari MT. Mazloomy Mahmoodabad SS, et al. Pak J Biol Sci. 2009 Nov 1;12(21):1430-3. doi: 10.3923/pjbs.2009.1430.1433. Pak J Biol Sci. 2009. PMID: 20128515 - Connecting Mobility to Infectious Diseases: The Promise and Limits of Mobile Phone Data.
Wesolowski A, Buckee CO, Engø-Monsen K, Metcalf CJE. Wesolowski A, et al. J Infect Dis. 2016 Dec 1;214(suppl_4):S414-S420. doi: 10.1093/infdis/jiw273. J Infect Dis. 2016. PMID: 28830104 Free PMC article. Review.
Cited by
- How human location-specific contact patterns impact spatial transmission between populations?
Wang L, Wang Z, Zhang Y, Li X. Wang L, et al. Sci Rep. 2013;3:1468. doi: 10.1038/srep01468. Sci Rep. 2013. PMID: 23511929 Free PMC article. - Malaria transmission modelling: a network perspective.
Liu J, Yang B, Cheung WK, Yang G. Liu J, et al. Infect Dis Poverty. 2012 Nov 1;1(1):11. doi: 10.1186/2049-9957-1-11. Infect Dis Poverty. 2012. PMID: 23849949 Free PMC article. - Design and methods of a social network isolation study for reducing respiratory infection transmission: The eX-FLU cluster randomized trial.
Aiello AE, Simanek AM, Eisenberg MC, Walsh AR, Davis B, Volz E, Cheng C, Rainey JJ, Uzicanin A, Gao H, Osgood N, Knowles D, Stanley K, Tarter K, Monto AS. Aiello AE, et al. Epidemics. 2016 Jun;15:38-55. doi: 10.1016/j.epidem.2016.01.001. Epub 2016 Feb 1. Epidemics. 2016. PMID: 27266848 Free PMC article. Clinical Trial. - Unsupervised user similarity mining in GSM sensor networks.
Shad SA, Chen E. Shad SA, et al. ScientificWorldJournal. 2013;2013:589610. doi: 10.1155/2013/589610. Epub 2013 Mar 18. ScientificWorldJournal. 2013. PMID: 23576905 Free PMC article. - Temporal aggregation impacts on epidemiological simulations employing microcontact data.
Hashemian M, Qian W, Stanley KG, Osgood ND. Hashemian M, et al. BMC Med Inform Decis Mak. 2012 Nov 15;12:132. doi: 10.1186/1472-6947-12-132. BMC Med Inform Decis Mak. 2012. PMID: 23153380 Free PMC article.
References
- Wasserman S, Faust K. Social Network Analysis: Methods and Applications. New York: Cambridge Univ Press; 1994.
- Kossinets G, Watts D. Empirical analysis of an evolving social network. Science. 2006;311:88–90. - PubMed
- Ebel H, Mielsch L, Bornholdt S. Scale-free topology of e-mail networks. Phys Rev E. 2002;66:35103. - PubMed
- Aiello W, Chung F, Lu L. Proceedings of the Thirty-Second Annual ACM Symposium on Theory of Computing. New York: Association for Computing Machinery; 2000. A random graph model for massive graphs; pp. 171–180.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources