Coarse-grained models reveal functional dynamics--I. Elastic network models--theories, comparisons and perspectives - PubMed (original) (raw)

Coarse-grained models reveal functional dynamics--I. Elastic network models--theories, comparisons and perspectives

Lee-Wei Yang et al. Bioinform Biol Insights. 2008.

Abstract

In this review, we summarize the progress on coarse-grained elastic network models (CG-ENMs) in the past decade. Theories were formulated to allow study of conformational dynamics in time/space frames of biological interest. Several highlighted models and their underlined hypotheses are introduced in physical depth. Important ENM offshoots, motivated to reproduce experimental data as well as to address the slow-mode-encoded configurational transitions, are also introduced. With the theoretical developments, computational cost is significantly reduced due to simplified potentials and coarse-grained schemes. Accumulating wealth of data suggest that ENMs agree equally well with experiment in describing equilibrium dynamics despite their distinct potentials and levels of coarse-graining. They however do differ in the slowest motional components that are essential to address large conformational changes of functional significance. The difference stems from the dissimilar curvatures of the harmonic energy wells described for each model. We also provide our views on the predictability of 'open to close' (open-->close) transitions of biomolecules on the basis of conformational selection theory. Lastly, we address the limitations of the ENM formalism which are partially alleviated by the complementary CG-MD approach, to be introduced in the second paper of this two-part series.

Keywords: B-factors; GNM; NMR; X-ray; low-frequency motions; normal mode analysis; potential surface.

PubMed Disclaimer

Figures

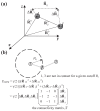
Figure S1.

Figure S1.

(a) The relative orientations of vectors R⃗ij, R⃗_ij_0and ΔR⃗i (b)The elastic potential of a tripeptide molecule, represented by Cα atoms only. The cutoff R c here is set small enough so that only the atom pairs (1,2) and (2,3) are in contact but not for (1,3). Practical GNM cutoff often takes a value between 6.5 and 15 Å. Provided a certain pair ij (i ≠ j) is in contact (their linear separation <R c), the off-diagonal element ij of the connectivity matrix Γ is set to −1; otherwise 0. The diagonal elements are the negative sums of the off-diagonal elements in each individual row (or column; since Γ is symmetric).

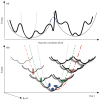
Figure 1

Figure 1

(a) The effect of simplified potentials. The energy landscape outlined by the conventional force field (detailed potential, as used by standard NMA) is drawn in thick lines. Simplified potential, (in thin lines) as used in Tirion’s or CG-EN models, approximates the rugged potential surface crossing the local energy barriers. At coarse-grained level, the rugged potential can be described by RTB/BNM and the smoothed-out one by XNM {X = A, βG, C, D and HE …}. Despite the difference between the two potentials, equilibrium dynamics characterized by X-ray and NMR can be well described by both potentials from which the derived slowest modes cover the slowest ends of experimentally observed dynamics (see Discussion). In contrast, the slowest modes derived from the smoothed-out potential are slower than those derived from the detailed potential due to the narrower energy wells in the latter. As a result, large conformational transitions with high anharmonicity could be better predicted by the slowest modes derived from the simple elastic potential than by force-field-based potential. The blue long dashed line joins the equal energy points of two CG energy wells as described by PNM (see Supplementary Material). (b) Similarity of the shape of hierarchical global potential envelopes. The thick lines indicate the actual detailed potential. The blue dotted line approximates the local energy well as in the standard NMA or ENMs. Green dashed and red dot-dashed lines approximate the potential envelopes at a higher hierarchy. The fractal-like similarity between the curvature of the local well and those of the potential envelopes at a higher hierarchy could account for part of the reason why NMA-based models, assuming a minimal structural deformation and approximating the potential of mean force harmonically at the equilibrium, can often predict large conformational changes reasonably well.

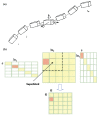
Figure 2

Figure 2

(a) Each block in the molecule is a rigid body that is subject to local translations/rotations (T/R) described by 6 T/R eigenvectors. The figure is reproduced from Durand et al. (1994) (b) The atomic Hessian matrix is expressed in a reduced basis for each coupled or diagonal block. Block i and j has _N_a,i and _N_a,j atoms, respectively. U i (part of the P matrix) is a _N_a,i by 6 matrix that consists of 6 T/R vectors, representing the rigid body motions of block i. The atomic Hessian elements for blocks i and j is projected to a 6 × 6 reduced Hessian H ij b using the equation H ij b = U iT H ij U j. Superblock, used in BNM, comprises several blocks. The Hessian elements within each superblock is computed on the fly and then projected to reduced dimension with P. The figure is reproduced from Durand et al. (1994) and Li and Cui, (2002).

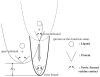
Figure 3

Figure 3

Conformational selection (Ma et al. 1999; Dror and Bahar, 2006) explains why open → close is easier predicted than close → open. Assuming only the protein takes the conformational change but ligand does not in either the bound or unbound state, the binary system, ligand + protein, evolves along the energy landscapes defined by (1) protein conformational change (with or without the contact of ligand) and (2) the binding energy ΔG, only. The conformational change is approximated harmonically by either atomic- or CG-ENM. “Close bound” state herein is referred to as ‘close state’ in the literature. Protein at the ‘open’ state access a close but unbound state (Dror and Bahar, 2006) along the smoothest deformational path (thin line), namely the slowest few normal modes. The protein in the disfavored “close unbound” state may further change the conformation a bit as being ‘induced’ by the ligand which then draws the whole binary system down to a new energy funnel at the big ΔG relief, in the end of the ligand docking. Since the architecture of protein is redefined by the newly formed contacts (Fig. 1 in Tama and Sanejouand, 2001), in either the “close unbound” or “close bound” (more so) state, the energy profiles (dash and solid lines, respectively) change their shape and curvature (mostly narrower) and the groups of atoms that undergo collective motions in the path open → close may not be identifiable again in the path close → open as NMA being performed on both of these close states. Not until the catalytic reaction on the substrate is complete or the ligand is released upon other chemical cues and in turn ‘pushes’ the structure back open, anharmonically, does the protein architecture resume its ‘open’ state again.

Similar articles

Cited by

References

    1. Arkhipov A, Freddolino PL, Schulten K. Stability and dynamics of virus capsids described by coarse-grained modeling. Structure. 2006a;14:1767–7. - PubMed
    1. Arkhipov A, Freddolino PL, Imada K, et al. Coarse-grained molecular dynamics simulations of a rotating bacterial flagellum. Biophys. J. 2006b;91:4589–97. - PMC - PubMed
    1. Brooks BR, Bruccoleri RE, Olafson BD, et al. CHARMM: A program for macromolecular energy, minimization and dynamics calculations. J. Comp. Chem. 1983;4:187–217.
    1. Chu JW, Voth GA. Coarse-grained free energy functions for studying protein conformational changes: a double-well network model. Biophys. J. BioFAST biophysj. 2007;107:112060. - PMC - PubMed
    1. Ikeguchi M, Ueno J, Sato M, et al. Protein structural change upon ligand binding: linear response theory. Phys Rev Lett. 2005;94:078102-1–4. - PubMed

LinkOut - more resources