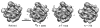Detecting consistent common lines in cryo-EM by voting - PubMed (original) (raw)

Detecting consistent common lines in cryo-EM by voting

Amit Singer et al. J Struct Biol. 2010 Mar.

Abstract

The single-particle reconstruction problem of electron cryo-microscopy (cryo-EM) is to find the three-dimensional structure of a macromolecule given its two-dimensional noisy projection images at unknown random directions. Ab initio estimates of the 3D structure are often obtained by the "Angular Reconstitution" method, in which a coordinate system is established from three projections, and the orientation of the particle giving rise to each image is deduced from common lines among the images. However, a reliable detection of common lines is difficult due to the low signal-to-noise ratio of the images. In this paper we describe a global self-correcting voting procedure in which all projection images participate to decide the identity of the consistent common lines. The algorithm determines which common line pairs were detected correctly and which are spurious. We show that the voting procedure succeeds at relatively low detection rates and that its performance improves as the number of projection images increases. We demonstrate the algorithm for both simulative and experimental images of the 50S ribosomal subunit.

(c) 2009 Elsevier Inc. All rights reserved.

PubMed Disclaimer

Figures

Figure 1

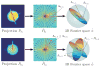
Figure 1

Fourier projection-slice theorem and its induced geometry. The Fourier transform of each projection P̂k corresponds to a planar slice through the three-dimensional Fourier transform φ̂ of the molecule. The Fourier transforms of any two projections P̂ _k_1 and P̂ _k_2 share a common line (Λ_k_1,_l_1 and Λ_k_2,_l_2), which is also a ray of the three-dimensional Fourier transform φ̂. Each Fourier ray Λ_k_1,_l_1 can be mapped to its direction vector β_k_1,_l_1. The direction vectors of the Fourier rays Λ_k_1,_l_1 and Λ_k_2,_l_2 that correspond to the common line between P _k_1 and P _k_2 must coincide, that is, β_k_1,_l_1 = β_k_2_l_2.

Figure 2

Figure 2

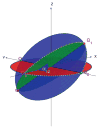
Angular Reconstitution: the common lines between P_1, P_2_, P_3 uniquely determine the angle _α_12 between _P_1 and _P_2 as well as the three intersection points _Q_12, _Q_13 and _Q_23 (“triangle”) of their corresponding great circles on the unit sphere (up to some three-dimensional rotation and possibly a reflection).

Figure 3

Figure 3

Simulated projection with various levels of additive Gaussian white noise.

Figure 4

Figure 4

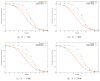
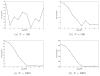
Comparing correlation filtering and histogram filtering for (a) N = 100, (b) N = 500, (c) N = 1000, (d) N = 5000.

Figure 5

Figure 5

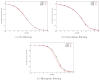
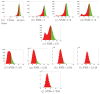
Smoothed histograms of the angle (in degrees) between pairs of projections. The plots were generated using N = 1000 projections with SNR=1/16. Top row corresponds to pairs of projections whose common lines were correctly identified. Bottom row corresponds to pairs of projections whose common lines were misidentified. Note the different scale of the _y_-axis in the two cases, indicating much higher peaks for correctly identified common-lines.

Figure 6

Figure 6

Common lines detection rate as a function of the SNR, for various values of N, when using (a) no filtering, (b) correlation filtering, (c) histogram filtering.

Figure 7

Figure 7

Running time (in seconds) of histogram filtering as a function of the SNR.

Figure 8

Figure 8

Histogram of peaks for N = 1000 and various levels of noise. The top p/2 percentile of each histogram is marked in Green, the bottom 1 − p/2 percentile is marked in Red, and the boundary between the regions is marked as a black vertical line. The location of the boundary is the minimal peak height to be considered by the algorithm as a correctly identified common line. Note how this threshold value decreases as the SNR decreases. The algorithm assumes that the correct common lines are concentrated in the Green area and that the wrong common lines are concentrated in the Red area.

Figure 9

Figure 9

Histogram of peaks for SNR = 1/16 for N = 100, 500, 1000, 5000.

Figure 10

Figure 10

Comparison of a refined model of the 50S ribosomal subunit with direct reconstructions from N = 750, 1500 and 3000 class averages. The refined model is from an Imagic reference-based alignment of the 27,121 particle data set used in this study and refined to 11.7Å resolution (3_σ_ criterion). The remaining structures were generated directly from the voting-derived common line assignments following classification into the given numbers of input classes. The voting-based structures, for the sake of comparison, were soft masked and filtered to 15Å resolution. The structures were also flipped about the _z_-axis such that their handedness is consistent with the X-ray structure [Ban N. et al., 2000] and shown as the Imagic-generated 3D volumes.

Figure 11

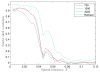
Figure 11

Fourier shell correlations of the various reconstructions.

Similar articles

Cited by

References

    1. Ban N, Nissen P, Hansen J, Moore PB, Steitz TA. The complete atomic structure of the large ribosomal subunit at 2.4 å resolution. Science. 2000;289:905–920. - PubMed
    1. Chiu W, Baker LM, Jiang W, Dougherty M, Schmid MF. Electron cryomicroscopy of biological machines at subnanometer resolution. Structure. 2005;13(3):363–372. review. - PubMed
    1. Coifman RR, Shkolnisky Y, Sigworth FJ, Singer A. Yale University, Department of Computer Science; 2007. Cryo-em structure determination through eigenvectors of sparse matrices. Technical Report 11, 1–42. URL http://www.cs.yale.edu/publications/techreports/tr1389.pdf.
    1. Farrow M, Ottensmeyer P. A posteriori determination of relative projection directions of arbitrarily oriented macrmolecules. Journal of the Optical Society of America A: Optics, Image Science, and Vision. 1992;9 (10):1749–1760.
    1. Frank J. Three-Dimensional Electron Microscopy of Macromolecular Assemblies: Visualization of Biological Molecules in Their Native State. Oxford: 2006.

Publication types

MeSH terms

LinkOut - more resources