A protocol for generating a high-quality genome-scale metabolic reconstruction - PubMed (original) (raw)
A protocol for generating a high-quality genome-scale metabolic reconstruction
Ines Thiele et al. Nat Protoc. 2010 Jan.
Abstract
Network reconstructions are a common denominator in systems biology. Bottom-up metabolic network reconstructions have been developed over the last 10 years. These reconstructions represent structured knowledge bases that abstract pertinent information on the biochemical transformations taking place within specific target organisms. The conversion of a reconstruction into a mathematical format facilitates a myriad of computational biological studies, including evaluation of network content, hypothesis testing and generation, analysis of phenotypic characteristics and metabolic engineering. To date, genome-scale metabolic reconstructions for more than 30 organisms have been published and this number is expected to increase rapidly. However, these reconstructions differ in quality and coverage that may minimize their predictive potential and use as knowledge bases. Here we present a comprehensive protocol describing each step necessary to build a high-quality genome-scale metabolic reconstruction, as well as the common trials and tribulations. Therefore, this protocol provides a helpful manual for all stages of the reconstruction process.
Figures
Figure 1. Overview of the procedure to iteratively reconstruct metabolic networks
In particular stages 2 to 4 are continuously iterated until model predictions are similar to the phenotypic characteristics of the target organism and/or all experimental data for comparison are exhausted.
Figure 2. Refinement of reconstruction content
The draft reconstruction is converted into a curated reconstruction by re-evaluation of the content. In particular, the metabolic reactions, obtained from biochemical databases or the literature, need to be tested for mass- and charge balancing. Many resources omit protons and water. Furthermore, adjusting metabolites to a particular pH may change their charged formulae and thus may require correction of the network reaction. For instance, the reaction catalyzed by the glucokinase which was obtained from KEGG is not mass- and charge-balanced when charged metabolite formula at pH 7.2 is considered. The right hand side (RHS) is missing an H and the charge is unbalanced. Adding a proton to the RHS balances both sides of the equation in terms of protons and electrons/charge. Abbreviations: glc – D-glucose, g6p – D-glucose-6-phosphate, atp – adenosine-triphosphate, adp – adenosine-diphosphate, H+ - proton. CS – confidence level.
Figure 3
List of functional groups, their charge formula and the corresponding pKa.
Figure 4. Examples of network evaluation
The network evaluation and debugging stage (stage 4) includes various QC/QA tests, some of which are illustrated in this figure. For instance, mass-and charge-balancing of the network reaction is crucial to ensure similar properties of the model and the cell or organism. A standard test for most metabolic reconstructions is to verify that each biomass precursor, which makes up a new cell, can be produced by the model in different growth conditions (e.g., minimal medium, different carbon sources, etc.). Other QC/QA tests may include the capability to secrete certain metabolites given a particular growth condition. At its end, the models will have similar properties as the cell and error cases can be used to systematically refine the models and thus the reconstruction content.
Figure 5. Gene-protein-reaction (GPR) associations
Examples of GPR associations and their representation in Boolean format are shown for E. coli.
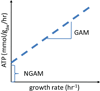
Figure 6. Growth associated maintentance (GAM) and non-growth associated maintenance (NGAM)
The best way to obtain accurate information regarding the GAM and NGAM is by plotting growth data obtained from chemostat growth experiments. GAM and NGAM can be directly read from the plot.
Figure 7. Conversion of reconstruction into a condition-specific model
This conversion requires three main steps. 1. The first step involves the mathematical representation by a stoichiometric matrix, S, of the network reaction list. The columns of S correspond to the network reactions, while the rows represent the network metabolites. The substrates in a reaction are defined to have a negative coefficient, while products have a positive value. The metabolites participating in a reaction have non-zero entry in the S matrix. 2. Now that the reconstruction is in a computer-readable format, the systems boundaries need to be defined. In particular, this means that for all metabolites that can be consumed or secreted by the target cell a so-called exchange reaction needs to be added to the reconstruction. The exchange reactions can be employed in later simulation to define for example environmental conditions (e.g., carbon source). 3. As a last step, constraints will be added to the reconstruction, thus rendering it to a condition-specific model. Mass conservation is a basic physical law. All steady-states can be thus described by S.v = 0 where v is a vector of reaction fluxes. Adding further constraints such as thermodynamics (reaction directionality), enzyme capacity or regulation (i.e., presence or absence of an enzyme) to the model will lead to a smaller, more confined set of feasible steady-states flux solutions.
Figure 8. Gap analysis
The gap analysis includes the identification and the tentative filling of network gaps. A. While many dead-end metabolites that create network gaps can be connected to the network by re-evaluating genomic and experimental data, some dead-end metabolites will remain in the refined, curated reconstruction. These dead-end metabolites can be grouped into two groups, depending on which type of reactions could connect them to the remaining network: knowledge gaps and scope gaps. While knowledge gaps represent missing biochemical knowledge for the target organism, the scope gaps include reactions and cellular processes, which are currently not accounted for in the metabolic reconstruction (e.g., DNA methylation). B. There are at least two approaches to identify gaps in the reconstruction. In the connectivity based approach, one can count the non-zero entries in each row of the S matrix and identify those metabolites, which are only produced or consumed. In the example, metabolite D is only produced by reaction v3 and the S matrix contains only one entry in the row corresponding to metabolite D. A second approach is based on model functionality: In this approach the models capability to carry flux through every network reaction is tested. This approach identifies blocked reactions, which are directly or indirectly associated with one or more dead-end metabolites. In the shown example, one would not identify metabolite E as a dead-end metabolite with the connectivity based approach as it is produced and consumed in the network. However, testing for flux through reactions containing E will show that reaction v3 and b3 cannot carry any flux in this model. C. Two sample cases are shown which address the question of filling a gap or not.
Figure 9. in silico gene essentiality study as network evaluation tool
While agreement of gene essentiality between experimental and in silico data is very helpful to validate the reconstruction content and model setup, analysis of the inconsistencies will enable discovery of new biological knowledge
Figure 10. Components of the model structure in Matlab
The reconstruction is imported into Matlab (Step 39). The entire reconstruction content is stored in a structure array. The screen shot illustrates the main fields contained in the model structure. The information is stored in subarrays in these fields. Note that the order of the reactions and metabolites corresponds to the order of columns and rows in the S matrix, respectively.
Figure 11. Flow chart to calculate the fractional contribution of a precursor to the biomass reaction
This approach can be used for amino acids, nucleotide triphosphates (ATP, GTP, CTP, UTP), and deoxy-nucleotide triphosphates (dATP, dGTP, dCTP, dTTP). The steps are illustrated for L-alanine (Ala). (A) The fractional contribution of alanine to the proteome is obtained from experimental data or estimated from genome sequence. (B) To convert the molar percentage into weight of alanine per mole protein, the molar percentage is multiplied by the molecular weight of alanine. Note that the polymerization of amino acid leads to the loss of a water molecule, which needs to be considered when calculating the molecular weight. Once the weight of amino acid per mole protein is obtained for all amino acids, they are summed to obtain the weight of protein per mole protein. (C) The weight of alanine per mole protein is converted into weight alanine per weight protein by multiplying with the sum of all amino acids’ weight. (D) Finally, the weight of alanine is multiplied by the cellular content of protein (see Figure 13A) and divided by its molecular weight to obtain the mole alanine per cell dry weight. Multiplying this molar contribution by a factor of 1000 will result in a final unit of mmol alanine per gram dry weight.
Figure 12. Determination of the content of soluble pool
Depending on the available information from literature, measurements or database entries the conversion into mmol/gDW and g/gDW is shown. The value in the purple box corresponds to the stoichiometric coefficient in the biomass reactions for the precursor. a Information was obtained from Cybercell Database (CCDB, see Table 1 for the link).
Figure 13. Determination of growth associated maintenance (GAM) cost
A. Calculation of growth-associated maintenance cost. B. Sample calculation for E. coli. The energy necessary for the synthesis of the macromolecules from the building blocks were obtained from Table 5 – 6 of Chapter 3 in Neidhardt et al.. The coefficient cP, cD, cR were calculating the total energy necessary for the macromolecules divided by the total number of building blocks (See Neidhardt et al.).
Figure 14. Flow chart on debugging network reactions that cannot carry flux
‘rxn ‘ stands for reaction. ‘conf’ stands for confidence score. ‘met’ stands for metabolite.
Similar articles
- Software platforms to facilitate reconstructing genome-scale metabolic networks.
Hamilton JJ, Reed JL. Hamilton JJ, et al. Environ Microbiol. 2014 Jan;16(1):49-59. doi: 10.1111/1462-2920.12312. Epub 2013 Nov 18. Environ Microbiol. 2014. PMID: 24148076 Review. - Reconciliation of genome-scale metabolic reconstructions for comparative systems analysis.
Oberhardt MA, Puchałka J, Martins dos Santos VA, Papin JA. Oberhardt MA, et al. PLoS Comput Biol. 2011 Mar;7(3):e1001116. doi: 10.1371/journal.pcbi.1001116. Epub 2011 Mar 31. PLoS Comput Biol. 2011. PMID: 21483480 Free PMC article. - BiGG: a Biochemical Genetic and Genomic knowledgebase of large scale metabolic reconstructions.
Schellenberger J, Park JO, Conrad TM, Palsson BØ. Schellenberger J, et al. BMC Bioinformatics. 2010 Apr 29;11:213. doi: 10.1186/1471-2105-11-213. BMC Bioinformatics. 2010. PMID: 20426874 Free PMC article. - The SuBliMinaL Toolbox: automating steps in the reconstruction of metabolic networks.
Swainston N, Smallbone K, Mendes P, Kell D, Paton N. Swainston N, et al. J Integr Bioinform. 2011 Nov 18;8(2):186. doi: 10.2390/biecoll-jib-2011-186. J Integr Bioinform. 2011. PMID: 22095399 - Understanding human metabolic physiology: a genome-to-systems approach.
Mo ML, Palsson BØ. Mo ML, et al. Trends Biotechnol. 2009 Jan;27(1):37-44. doi: 10.1016/j.tibtech.2008.09.007. Epub 2008 Nov 17. Trends Biotechnol. 2009. PMID: 19010556 Review.
Cited by
- Using Genome-scale Models to Predict Biological Capabilities.
O'Brien EJ, Monk JM, Palsson BO. O'Brien EJ, et al. Cell. 2015 May 21;161(5):971-987. doi: 10.1016/j.cell.2015.05.019. Cell. 2015. PMID: 26000478 Free PMC article. Review. - Metabolic stasis in an ancient symbiosis: genome-scale metabolic networks from two Blattabacterium cuenoti strains, primary endosymbionts of cockroaches.
González-Domenech CM, Belda E, Patiño-Navarrete R, Moya A, Peretó J, Latorre A. González-Domenech CM, et al. BMC Microbiol. 2012 Jan 18;12 Suppl 1(Suppl 1):S5. doi: 10.1186/1471-2180-12-S1-S5. BMC Microbiol. 2012. PMID: 22376077 Free PMC article. - 13C Metabolic Flux Analysis for Systematic Metabolic Engineering of S. cerevisiae for Overproduction of Fatty Acids.
Ghosh A, Ando D, Gin J, Runguphan W, Denby C, Wang G, Baidoo EE, Shymansky C, Keasling JD, García Martín H. Ghosh A, et al. Front Bioeng Biotechnol. 2016 Oct 5;4:76. doi: 10.3389/fbioe.2016.00076. eCollection 2016. Front Bioeng Biotechnol. 2016. PMID: 27761435 Free PMC article. - Efficient Reconstruction of Predictive Consensus Metabolic Network Models.
van Heck RG, Ganter M, Martins Dos Santos VA, Stelling J. van Heck RG, et al. PLoS Comput Biol. 2016 Aug 26;12(8):e1005085. doi: 10.1371/journal.pcbi.1005085. eCollection 2016 Aug. PLoS Comput Biol. 2016. PMID: 27563720 Free PMC article. - HEPNet: A Knowledge Base Model of Human Energy Pool Network for Predicting the Energy Availability Status of an Individual.
Sengupta A, Grover M, Chakraborty A, Saxena S. Sengupta A, et al. PLoS One. 2015 Jun 8;10(6):e0127918. doi: 10.1371/journal.pone.0127918. eCollection 2015. PLoS One. 2015. PMID: 26053019 Free PMC article.
References
- Almaas E, Kovacs B, Vicsek T, Oltvai ZN, Barabasi AL. Global organization of metabolic fluxes in the bacterium Escherichia coli. Nature. 2004;427:839–843. - PubMed
- Thiele I, Price ND, Vo TD, Palsson BO. Candidate metabolic network states in human mitochondria: Impact of diabetes, ischemia, and diet. J Biol Chem. 2005;280:11683–11695. - PubMed
- Pal C, et al. Chance and necessity in the evolution of minimal metabolic networks. Nature. 2006;440:667–670. - PubMed
- Covert MW, Knight EM, Reed JL, Herrgard MJ, Palsson BO. Integrating high-throughput and computational data elucidates bacterial networks. Nature. 2004;429:92–96. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources