Membrane curvature controls dynamin polymerization - PubMed (original) (raw)

Membrane curvature controls dynamin polymerization

Aurélien Roux et al. Proc Natl Acad Sci U S A. 2010.

Abstract

The generation of membrane curvature in intracellular traffic involves many proteins that can curve lipid bilayers. Among these, dynamin-like proteins were shown to deform membranes into tubules, and thus far are the only proteins known to mechanically drive membrane fission. Because dynamin forms a helical coat circling a membrane tubule, its polymerization is thought to be responsible for this membrane deformation. Here we show that the force generated by dynamin polymerization, 18 pN, is sufficient to deform membranes yet can still be counteracted by high membrane tension. Importantly, we observe that at low dynamin concentration, polymer nucleation strongly depends on membrane curvature. This suggests that dynamin may be precisely recruited to membrane buds' necks because of their high curvature. To understand this curvature dependence, we developed a theory based on the competition between dynamin polymerization and membrane mechanical deformation. This curvature control of dynamin polymerization is predicted for a specific range of concentrations ( approximately 0.1-10 microM), which corresponds to our measurements. More generally, we expect that any protein that binds or self-assembles onto membranes in a curvature-coupled way should behave in a qualitatively similar manner, but with its own specific range of concentration.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Fig. 1.

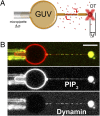
Fig. 1.

Experimental setup. (A) Schematic drawing of the experimental setup. A micropipette controls the GUV tension, Δσ, while optical tweezers are used to extract a membrane tube and measure the force needed to hold the tube (Δ_f_) as dynamin (red) polymerizes along it. The distribution of dynamin is simultaneously measured via confocal imaging. (B) Typical dual-color image of a GUV labeled with GloPIP2 (red channel) and dynamin labeled with Alexa 488 (green channel). Inhomogeneities in the red channel are due to bleedthrough from the green channel to the red. (Scale bar, 10 μm.)

Fig. 2.

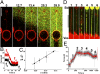
Fig. 2.

Dynamin polymerization force measurements. (A) Sequence of confocal images following the injection of fluorescent dynamin (green; 12 μM) in the vicinity of a tube pulled from a GUV (time in seconds). (B) Plot of tube-holding force versus time after injection of dynamin (t = 0) shown for two vesicles with different membrane tensions. Dynamin rapidly reduces the tube-holding force from its initial value, fb, to a lower final level, fd (see text). (C) Plot of fd versus membrane tension showing a linear dependence (11 GUVs). (D) Images of a nucleation/growth process occurring for a dynamin concentration of 440 nM. Following a few stepwise increases of aspiration pressure (1), dots of dynamin appear on the tube (2). With the aspiration then held constant, the dynamin clusters continue to grow (2–4) until full coverage is reached (5). (E) Plot of force (smoothed average, red; raw data, gray) versus time for the experiment presented in D. The force starts to drop when dynamin fully covers the tube (5). (Scale bars, 10 μm.)

Fig. 3.

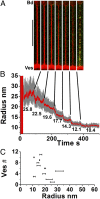
Fig. 3.

Curvature control of dynamin nucleation. Images of the membrane tube (A) (membrane, red; dynamin, green) following each stepwise reduction of tube radius (nm) as indicated in B. Polymerization of dynamin is only visible for the smallest tube radius. (Scale bar, 10 μm.) (C) Critical radius windows obtained from 11 vesicles.

Fig. 4.

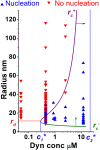
Fig. 4.

Phase diagram of dynamin nucleation as a function of tube radius and dynamin concentration. Experimental results are marked with triangles (red, inverted = no nucleation; blue, upright = nucleation). Boundaries of the region of dynamin nucleation, rc+ (purple line, arrow) and rc− (green line, arrow), were calculated for the theoretical model: formula image and formula image (

SI Mathematical Modeling

). Nucleation should not occur below the lower concentration, _c_1*. Above the higher concentration, _c_2*, nucleation should always occur, independent of membrane tube radius. rd corresponds to the internal radius of a dynamin-coated membrane tube.

Similar articles

Cited by

References

    1. Antonny B. Membrane deformation by protein coats. Curr Opin Cell Biol. 2006;18:386–394. - PubMed
    1. Zimmerberg J, Kozlov MM. How proteins produce cellular membrane curvature. Nat Rev Mol Cell Biol. 2006;7:9–19. - PubMed
    1. Takei K, McPherson PS, Schmid SL, De Camilli P. Tubular membrane invaginations coated by dynamin rings are induced by GTP-γ S in nerve terminals. Nature. 1995;374:186–190. - PubMed
    1. Pucadyil TJ, Schmid SL. Real-time visualization of dynamin-catalyzed membrane fission and vesicle release. Cell. 2008;135:1263–1275. - PMC - PubMed
    1. Bashkirov PV, et al. GTPase cycle of dynamin is coupled to membrane squeeze and release, leading to spontaneous fission. Cell. 2008;135:1276–1286. - PMC - PubMed

Publication types

MeSH terms

Substances

LinkOut - more resources