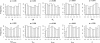ABCtoolbox: a versatile toolkit for approximate Bayesian computations - PubMed (original) (raw)
ABCtoolbox: a versatile toolkit for approximate Bayesian computations
Daniel Wegmann et al. BMC Bioinformatics. 2010.
Abstract
Background: The estimation of demographic parameters from genetic data often requires the computation of likelihoods. However, the likelihood function is computationally intractable for many realistic evolutionary models, and the use of Bayesian inference has therefore been limited to very simple models. The situation changed recently with the advent of Approximate Bayesian Computation (ABC) algorithms allowing one to obtain parameter posterior distributions based on simulations not requiring likelihood computations.
Results: Here we present ABCtoolbox, a series of open source programs to perform Approximate Bayesian Computations (ABC). It implements various ABC algorithms including rejection sampling, MCMC without likelihood, a Particle-based sampler and ABC-GLM. ABCtoolbox is bundled with, but not limited to, a program that allows parameter inference in a population genetics context and the simultaneous use of different types of markers with different ploidy levels. In addition, ABCtoolbox can also interact with most simulation and summary statistics computation programs. The usability of the ABCtoolbox is demonstrated by inferring the evolutionary history of two evolutionary lineages of Microtus arvalis. Using nuclear microsatellites and mitochondrial sequence data in the same estimation procedure enabled us to infer sex-specific population sizes and migration rates and to find that males show smaller population sizes but much higher levels of migration than females.
Conclusion: ABCtoolbox allows a user to perform all the necessary steps of a full ABC analysis, from parameter sampling from prior distributions, data simulations, computation of summary statistics, estimation of posterior distributions, model choice, validation of the estimation procedure, and visualization of the results.
Figures
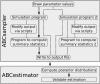
Figure 1
Flowchart describing the individual steps of an ABC estimation by ABCtoolbox. Black arrows indicate the standard approach. Some alternative paths are shown with dotted lines. For instance, it is possible to modify the output of a simulation program such as to allow one to take specific characteristics of the observed data into account such as a given level of missing data. Additionally, ABCtoolbox can call several simulation programs per iteration, each of which can be launched with the same parameter values. Thus, different data types can be conveniently combined in a single analysis.
Figure 2
Evolutionary model of the demographic history of two groups of populations corresponding to the Central and Eastern mtDNA evolutionary lineages of the common vole Microtus arvalis. An ancestral population of size N A diverges into the two population groups T DIV generations ago. We assumed a continent-island model for each of the two population groups. Islands (numbered subscripts) represent populations from which genetic data is available and the continents (subscripts "Eastern" and "Central") represent collectively all unsampled populations from a given evolutionary lineage. We further assumed the population sizes of the continents (_N_Central and _N_Eastern) to be large (107 individuals) and the population sizes of the islands (N1, N2, N3, etc.) to follow a Normal distribution with mean N and standard deviation σ N. Note that only four out of the 11 islands are shown. Backward in time, migration was only allowed from islands to the continent at rates Nm. While the same demographic model was assumed for both marker types, population sizes and migration rates were scaled differently (see text).
Figure 3
Distributions of the quantiles (_x_-axis) of the known parameter values as inferred from the posterior distributions obtained with ABCestimator for 1000 pseudo-observed data sets. These distributions are expected to be uniform if posterior densities have appropriate coverage properties [9]. We show these distributions for all model parameters (see text). The reported p-values above each histogram are the result of a Kolmogorov-Smirnov test for departure from distribution uniformity.
Figure 4
Posterior distributions obtained with ABCestimator based on a likelihood-free MCMC chain of 106 steps performed by ABCsampler. Additional characteristics of the posterior distributions, along with the prior distributions, are given in Table 1. See Figure 2 and text for parameter description.
Similar articles
- Complex genetic admixture histories reconstructed with Approximate Bayesian Computation.
Fortes-Lima CA, Laurent R, Thouzeau V, Toupance B, Verdu P. Fortes-Lima CA, et al. Mol Ecol Resour. 2021 May;21(4):1098-1117. doi: 10.1111/1755-0998.13325. Epub 2021 Feb 26. Mol Ecol Resour. 2021. PMID: 33452723 Free PMC article. - Estimation of evolutionary parameters using short, random and partial sequences from mixed samples of anonymous individuals.
Wu SH, Rodrigo AG. Wu SH, et al. BMC Bioinformatics. 2015 Nov 4;16:357. doi: 10.1186/s12859-015-0810-y. BMC Bioinformatics. 2015. PMID: 26536860 Free PMC article. - Inference on population history and model checking using DNA sequence and microsatellite data with the software DIYABC (v1.0).
Cornuet JM, Ravigné V, Estoup A. Cornuet JM, et al. BMC Bioinformatics. 2010 Jul 28;11:401. doi: 10.1186/1471-2105-11-401. BMC Bioinformatics. 2010. PMID: 20667077 Free PMC article. - On the use of kernel approximate Bayesian computation to infer population history.
Nakagome S. Nakagome S. Genes Genet Syst. 2015;90(3):153-62. doi: 10.1266/ggs.90.153. Genes Genet Syst. 2015. PMID: 26510570 Review. - ABC as a flexible framework to estimate demography over space and time: some cons, many pros.
Bertorelle G, Benazzo A, Mona S. Bertorelle G, et al. Mol Ecol. 2010 Jul;19(13):2609-25. doi: 10.1111/j.1365-294X.2010.04690.x. Epub 2010 Jun 18. Mol Ecol. 2010. PMID: 20561199 Review.
Cited by
- Contribution of Spontaneous Mutations to Quantitative and Molecular Variation at the Highly Repetitive rDNA Locus in Yeast.
Sharp NP, Smith DR, Driscoll G, Sun K, Vickerman CM, Martin SCT. Sharp NP, et al. Genome Biol Evol. 2023 Oct 6;15(10):evad179. doi: 10.1093/gbe/evad179. Genome Biol Evol. 2023. PMID: 37847861 Free PMC article. - Joint inference of evolutionary transitions to self-fertilization and demographic history using whole-genome sequences.
Strütt S, Sellinger T, Glémin S, Tellier A, Laurent S. Strütt S, et al. Elife. 2023 May 11;12:e82384. doi: 10.7554/eLife.82384. Elife. 2023. PMID: 37166007 Free PMC article. - The mutual history of Schlegel's Japanese gecko (Reptilia: Squamata: Gekkonidae) and humans inscribed in genes and ancient literature.
Chiba M, Hirano T, Yamazaki D, Ye B, Ito S, Kagawa O, Endo K, Nishida S, Hara S, Aratake K, Chiba S. Chiba M, et al. PNAS Nexus. 2022 Nov 30;1(5):pgac245. doi: 10.1093/pnasnexus/pgac245. eCollection 2022 Nov. PNAS Nexus. 2022. PMID: 36712337 Free PMC article. - Species delineation and genetic structure of two Chaerephon species (C. pusillus and C. leucogaster) on Madagascar and the Comoro archipelago.
Tidière M, Portanier E, Jacquet S, Goodman SM, Monnier G, Beuneux G, Desmet JF, Kaerle C, Queney G, Barataud M, Pontier D. Tidière M, et al. Ecol Evol. 2022 Dec 3;12(12):e9566. doi: 10.1002/ece3.9566. eCollection 2022 Dec. Ecol Evol. 2022. PMID: 36479032 Free PMC article. - Genetic structure and differentiation from early bronze age in the mediterranean island of sicily: Insights from ancient mitochondrial genomes.
Modi A, Vizzari MT, Catalano G, Boscolo Agostini R, Vai S, Lari M, Vergata C, Zaro V, Liccioli L, Fedi M, Barone S, Nigro L, Lancioni H, Achilli A, Sineo L, Caramelli D, Ghirotto S. Modi A, et al. Front Genet. 2022 Sep 9;13:945227. doi: 10.3389/fgene.2022.945227. eCollection 2022. Front Genet. 2022. PMID: 36159977 Free PMC article.
References
- Pritchard JK, Seielstad MT, Perez-Lezaun A, Feldman MW. Population growth of human Y chromosomes: a study of Y chromosome microsatellites. Mol Biol Evol. 1999;16(12):1791–1798. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources