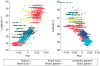Variance component model to account for sample structure in genome-wide association studies - PubMed (original) (raw)
Variance component model to account for sample structure in genome-wide association studies
Hyun Min Kang et al. Nat Genet. 2010 Apr.
Abstract
Although genome-wide association studies (GWASs) have identified numerous loci associated with complex traits, imprecise modeling of the genetic relatedness within study samples may cause substantial inflation of test statistics and possibly spurious associations. Variance component approaches, such as efficient mixed-model association (EMMA), can correct for a wide range of sample structures by explicitly accounting for pairwise relatedness between individuals, using high-density markers to model the phenotype distribution; but such approaches are computationally impractical. We report here a variance component approach implemented in publicly available software, EMMA eXpedited (EMMAX), that reduces the computational time for analyzing large GWAS data sets from years to hours. We apply this method to two human GWAS data sets, performing association analysis for ten quantitative traits from the Northern Finland Birth Cohort and seven common diseases from the Wellcome Trust Case Control Consortium. We find that EMMAX outperforms both principal component analysis and genomic control in correcting for sample structure.
Conflict of interest statement
COMPETING FINANCIAL INTERESTS The authors declare no competing financial interests.
Figures
Figure 1
Scatter plots of the first two principal components against latitude and longitude. Only individuals of known ancestry are included in the plot. Latitude and longitude are defined as the average latitude and longitude of the parents’ birthplaces. Colors indicate linguistic or geographic subgroups.
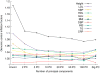
Figure 2
The genomic control parameters for ten traits change with the number of principal components used for adjustment. Sig PC, significant principal components, includes the principal components (PC) that have a _t_-test P value < 0.005 as predictors for each of the phenotypes. LDL, low density lipoprotein; SBP, systolic blood pressure; HDL, high-density lipoprotein; GLU, glucose; BMI, body mass index; DBP, diastolic blood pressure; INS, insulin plasma levels; TG, triglyceride; CRP, C-reactive protein.
Figure 3
Comparison of P value distributions across different methods with NFBC66 data. (a) Quantile-quantile plot of the height phenotype, which shows the largest inflation of test statistics, before application of genomic control. The shadowed region represents a conservative 95% confidence interval (CI) computed from the beta distribution assuming independence markers. ES100 indicates EIGENSOFT correcting for 100 principal components. (b) Comparison of LDL association P values between uncorrected and EMMAX analysis after application of genomic control in a logarithmic scale.
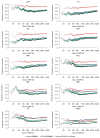
Figure 4
Rank concordance comparison of strongly associated SNPs between different methods. The ten NFBC66 phenotypes (abbreviated as in Fig. 2) are ordered by their genomic control inflation factors. Rank concordance is presented as CAT plots. The proportion of SNPs shared between sets of the top k SNPs for different methods are shown for 10 ≤ k ≤ 5000. Pairs of sets being compared are indicated in key at bottom; for example, Uncorr-EMMAX, comparison of uncorrected set and EMMAX set. ES100 indicates EIGENSOFT correcting for 100 principal components.
Figure 5
Distribution of the marker-specific inflation factors from NFBC66 data sets. (a) Box plots of the marker-specific inflation factors across ten phenotypes, in addition to the genomic control inflation factor for each phenotype. Abbreviations are as in Figure 2. (b,c) Distributions of P values of the height phenotype association when the estimated per-marker inflation factors are less than 1.05 (35,988 SNPs; b) and when they are greater than 1.2 (15,874 SNPs; c).
Similar articles
- Genome-wide efficient mixed-model analysis for association studies.
Zhou X, Stephens M. Zhou X, et al. Nat Genet. 2012 Jun 17;44(7):821-4. doi: 10.1038/ng.2310. Nat Genet. 2012. PMID: 22706312 Free PMC article. - Novel probabilistic models of spatial genetic ancestry with applications to stratification correction in genome-wide association studies.
Bhaskar A, Javanmard A, Courtade TA, Tse D. Bhaskar A, et al. Bioinformatics. 2017 Mar 15;33(6):879-885. doi: 10.1093/bioinformatics/btw720. Bioinformatics. 2017. PMID: 28025204 Free PMC article. - An efficient multi-locus mixed-model approach for genome-wide association studies in structured populations.
Segura V, Vilhjálmsson BJ, Platt A, Korte A, Seren Ü, Long Q, Nordborg M. Segura V, et al. Nat Genet. 2012 Jun 17;44(7):825-30. doi: 10.1038/ng.2314. Nat Genet. 2012. PMID: 22706313 Free PMC article. - Software engineering the mixed model for genome-wide association studies on large samples.
Zhang Z, Buckler ES, Casstevens TM, Bradbury PJ. Zhang Z, et al. Brief Bioinform. 2009 Nov;10(6):664-75. doi: 10.1093/bib/bbp050. Brief Bioinform. 2009. PMID: 19933212 Review. - Statistical methods for genome-wide and sequencing association studies of complex traits in related samples.
Thornton TA. Thornton TA. Curr Protoc Hum Genet. 2015 Jan 20;84:1.28.1-1.28.9. doi: 10.1002/0471142905.hg0128s84. Curr Protoc Hum Genet. 2015. PMID: 25599666 Free PMC article. Review.
Cited by
- Releasing a sugar brake generates sweeter tomato without yield penalty.
Zhang J, Lyu H, Chen J, Cao X, Du R, Ma L, Wang N, Zhu Z, Rao J, Wang J, Zhong K, Lyu Y, Wang Y, Lin T, Zhou Y, Zhou Y, Zhu G, Fei Z, Klee H, Huang S. Zhang J, et al. Nature. 2024 Nov 13. doi: 10.1038/s41586-024-08186-2. Online ahead of print. Nature. 2024. PMID: 39537922 - Multiomics dissection of Brassica napus L. lateral roots and endophytes interactions under phosphorus starvation.
Liu C, Bai Z, Luo Y, Zhang Y, Wang Y, Liu H, Luo M, Huang X, Chen A, Ma L, Chen C, Yuan J, Xu Y, Zhu Y, Mu J, An R, Yang C, Chen H, Chen J, Li Z, Li X, Dong Y, Zhao J, Shen X, Jiang L, Feng X, Yu P, Wang D, Chen X, Li N. Liu C, et al. Nat Commun. 2024 Nov 10;15(1):9732. doi: 10.1038/s41467-024-54112-5. Nat Commun. 2024. PMID: 39523413 Free PMC article. - Genome-Wide Association-Based Identification of Alleles, Genes and Haplotypes Influencing Yield in Rice (Oryza sativa L.) Under Low-Phosphorus Acidic Lowland Soils.
James M, Tyagi W, Magudeeswari P, Neeraja CN, Rai M. James M, et al. Int J Mol Sci. 2024 Oct 30;25(21):11673. doi: 10.3390/ijms252111673. Int J Mol Sci. 2024. PMID: 39519225 Free PMC article. - Structural variation reshapes population gene expression and trait variation in 2,105 Brassica napus accessions.
Zhang Y, Yang Z, He Y, Liu D, Liu Y, Liang C, Xie M, Jia Y, Ke Q, Zhou Y, Cheng X, Huang J, Liu L, Xiang Y, Raman H, Kliebenstein DJ, Liu S, Yang QY. Zhang Y, et al. Nat Genet. 2024 Nov;56(11):2538-2550. doi: 10.1038/s41588-024-01957-7. Epub 2024 Nov 5. Nat Genet. 2024. PMID: 39501128 Free PMC article. - Causal effect of psoriasis on aortic valve stenosis: a two-sample Mendelian randomization study.
Jiang KX, Wang Y, Liu YT, Xu Y, Huang FY, Chen M. Jiang KX, et al. J Geriatr Cardiol. 2024 Sep 28;21(9):865-873. doi: 10.26599/1671-5411.2024.09.002. J Geriatr Cardiol. 2024. PMID: 39483265 Free PMC article.
References
- Weir BS, Anderson AD, Hepler AB. Genetic relatedness analysis: modern data and new challenges. Nat Rev Genet. 2006;7:771–780. - PubMed
- Helgason A, Yngvadttir B, Hrafnkelsson B, Gulcher J, Stefnsson K. An Icelandic example of the impact of population structure on association studies. Nat Genet. 2005;37:90–95. - PubMed
Publication types
MeSH terms
Grants and funding
- N01ES45530/ES/NIEHS NIH HHS/United States
- P30 1MH083268/MH/NIMH NIH HHS/United States
- HL087679-01/HL/NHLBI NIH HHS/United States
- 5PL1NS062410-03/NS/NINDS NIH HHS/United States
- R01 HL087679/HL/NHLBI NIH HHS/United States
- NH084698/NH/NIH HHS/United States
- U01-DA024417/DA/NIDA NIH HHS/United States
- UL1 DE019580/DE/NIDCR NIH HHS/United States
- 6R01HL087679-03/HL/NHLBI NIH HHS/United States
- K25 HL080079-05/HL/NHLBI NIH HHS/United States
- K25 HL080079/HL/NHLBI NIH HHS/United States
- GM053275-14/GM/NIGMS NIH HHS/United States
- U01 DA024417/DA/NIDA NIH HHS/United States
- 1K25HL080079/HL/NHLBI NIH HHS/United States
- PL1 NS062410/NS/NINDS NIH HHS/United States
- 5RL1MH083268-03/MH/NIMH NIH HHS/United States
- 5UL1DE019580-03/DE/NIDCR NIH HHS/United States
- RL1 MH083268/MH/NIMH NIH HHS/United States
- R01 GM053275/GM/NIGMS NIH HHS/United States
LinkOut - more resources
Full Text Sources
Other Literature Sources