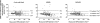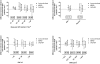Performance of the Cockcroft-Gault, MDRD, and new CKD-EPI formulas in relation to GFR, age, and body size - PubMed (original) (raw)

Comparative Study

Performance of the Cockcroft-Gault, MDRD, and new CKD-EPI formulas in relation to GFR, age, and body size

Wieneke Marleen Michels et al. Clin J Am Soc Nephrol. 2010 Jun.

Abstract

Background and objectives: We compared the estimations of Cockcroft-Gault, Modification of Diet in Renal Disease (MDRD), and Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) equations to a gold standard GFR measurement using (125)I-iothalamate, within strata of GFR, gender, age, body weight, and body mass index (BMI).

Design, setting, participants, & measurements: For people who previously underwent a GFR measurement, bias, precision, and accuracies between measured and estimated kidney functions were calculated within strata of the variables. The relation between the absolute bias and the variables was tested with linear regression analysis.

Results: Overall (n = 271, 44% male, mean measured GFR 72.6 ml/min per 1.73 m(2) [SD 30.4 ml/min per 1.73 m(2)]), mean bias was smallest for MDRD (P < 0.01). CKD-EPI had highest accuracy (P < 0.01 compared with Cockcroft-Gault), which did not differ from MDRD (P = 0.14). The absolute bias of all formulas was related to age. For MDRD and CKD-EPI, absolute bias was also related to the GFR; for Cockcroft-Gault, it was related to body weight and BMI as well. In all extreme subgroups, MDRD and CKD-EPI provided highest accuracies.

Conclusions: The absolute bias of all formulas is influenced by age; CKD-EPI and MDRD are also influenced by GFR. Cockcroft-Gault is additionally influenced by body weight and BMI. In general, CKD-EPI gives the best estimation of GFR, although its accuracy is close to that of the MDRD.

PubMed Disclaimer

Figures

Figure 1.

Figure 1.

Bland-Altman figures of the estimated and measured kidney function. Bland-Altman plots—the difference between the estimated and measured renal function—is plotted against the measured GFR; therefore, a positive difference suggests an overestimation by the formula, whereas a negative difference suggests an underestimation. The dashed lines represent the mean difference between estimated and measured GFR; the solid lines represent the lines of agreement, calculated as mean difference plus or minus two times the SD of this difference.

Figure 2.

Figure 2.

Comparison of the bias and precisions over subgroups. Mean bias and precision between estimated and measured GFR for to various strata of GFR, gender, age, and BMI. The mean bias was calculated as the mean of the differences between the estimated and measured GFR per subgroup, whereas the precision was the SD of this difference.

Comment in

Similar articles

Cited by

References

    1. Fawaz A, Badr KF: Measuring filtration function in clinical practice. Curr Opin Nephrol Hypertens 15: 643–647, 2006 - PubMed
    1. Levey AS, Coresh J, Greene T, Stevens LA, Zhang YL, Hendriksen S, Kusek JW, Van Lente F: Using standardized serum creatinine values in the Modification of Diet in Renal Disease study equation for estimating glomerular filtration rate. Ann Intern Med 145: 247–254, 2006 - PubMed
    1. Cockcroft DW, Gault MH: Prediction of creatinine clearance from serum creatinine. Nephron 16: 31–41, 1976 - PubMed
    1. Boudville N, Salama M, Jeffrey GP, Ferrari P: The inaccuracy of cystatin C and creatinine-based equations in predicting GFR in orthotopic liver transplant recipients. Nephrol Dial Transplant 24: 2926–2930, 2009 - PubMed
    1. Donadio C, Consani C, Ardini M, Caprio F, Grassi G, Lucchesi A: Prediction of glomerular filtration rate from body cell mass and plasma creatinine. Curr Drug Discov Technol 1: 221–228, 2004 - PubMed

Publication types

MeSH terms

Substances

LinkOut - more resources