Foldable structures and the natural design of pollen grains - PubMed (original) (raw)
Foldable structures and the natural design of pollen grains
Eleni Katifori et al. Proc Natl Acad Sci U S A. 2010.
Abstract
Upon release from the anther, pollen grains of angiosperm flowers are exposed to a dry environment and dehydrate. To survive this process, pollen grains possess a variety of physiological and structural adaptations. Perhaps the most striking of these adaptations is the ability of the pollen wall to fold onto itself to prevent further desiccation. Roger P. Wodehouse coined the term harmomegathy for this folding process in recognition of the critical role it plays in the survival of the pollen grain. There is still, however, no quantitative theory that explains how the structure of the pollen wall contributes to harmomegathy. Here we demonstrate that simple geometrical and mechanical principles explain how wall structure guides pollen grains toward distinct folding pathways. We found that the presence of axially elongated apertures of high compliance is critical for achieving a predictable and reversible folding pattern. Moreover, the intricate sculpturing of the wall assists pollen closure by preventing mirror buckling of the surface. These results constitute quantitative structure-function relationships for pollen harmomegathy and provide a framework to elucidate the functional significance of the very diverse pollen morphologies observed in angiosperms.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
Fig. 1.
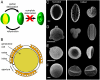
Harmomegathy in pollen grains. (A) Folding of aperturate pollen grains in response to change in humidity allows a partial dehydration of the cellular material while preventing complete desiccation and death. (B) Wall structure of a typical tricolpate (tri- aperturate) pollen grain. (C)—(F) SEM images of pollen grains in their unfolded (hydrated) and folded states. (C) The monosulcate pollen grain of Lilium longiflorum. In the hydrated state, the intine is visible at the aperture, where the exine is absent. In the folded state, the aperture has invaginated. (D) The tricolpate pollen grain of Euphorbia milii. The aperture protrudes in the hydrated state but retracts completely within the pollen in the folded state. (E) The inaperturate pollen of Aristolochia gigantea. Harmomegathy is reduced to a mirror buckling of the pollen wall. (F) The monoporate pollen grain of maize (Zea mays). Scale bar, 20 μm.
Fig. 2.
Folding pathways for monosulcate pollen (Lilium longiflorum, left) and tricolpate pollen (Euphorbia milii, right). (A) and (D) Sequential scanning electron micrographs of desiccating lily and euphorbia pollen grains. (B) and (E) Inextensional solutions for the exine folding. (C) and (F) Numerical simulations of the folding. (G) The “monosulcate fold” as observed in lily pollen. Step 1: rotate the meridional outline of the hydrated pollen grain around the pollen axis to create a surface of revolution. Step 2: remove the segment corresponding to the aperture. Step 3: fold the surface using the relation r = _αr_0 with α < 1. (_H_) The tricolpate fold as observed in euphorbia pollen. Step 1: rotate the equatorial outline of one of the three interapertural regions around the axis to create a surface of revolution. Step 2: excise three segments corresponding to the interapertural exine (light regions) to assemble a complete hydrated pollen grain. Step 3: fold the surface using the relation _r_ = _αr_0 with _α_ > 1 and excise the three segments corresponding to the interapertural exine to assemble a complete folded pollen grain.
Fig. 3.
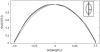
Normalization of the lily pollen grain meridional outlines by the equatorial radius. All curves collapse onto one master curve. Inset, pollen grain meridional outlines (hydrated and fully folded) in Cartesian coordinates. The outlines were obtained from environmental scanning electron micrographs.
Fig. 4.
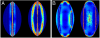
Stretching and bending energies in folded pollen grains. (A) Computed bending (left) and stretching (right) energy densities in the lily pollen grain. (B) Computed bending (left) and stretching (right) energy densities in the euphorbia pollen grain. Red indicates high energy density (note: the energy scales are in arbitrary units but are kept constant in (A) and (B).
Fig. 5.
Energetics of pollen wall deformation for different apertural shapes. The initial geometry of the pollen grain (ellipsoid of revolution, ratio of long R L to short R axis equal to R L/R = 1.2), ratio of bending moduli of intine κ I, and exine κ E equal to κ I/κ E = 0.015, thicknesses h E/R = 1/50 and h I/R = 1/25 are the same for (A)–(E). The top row represents the turgid geometry, the lighter color indicating the position of the aperture. The middle and bottom rows indicate the stretching and bending energy density of the exine, respectively (orange color: high energy; blue color: low energy). The color scheme for the stretching and bending energy density is in arbitrary units but was kept constant for all the cases shown.
Fig. 6.
The network of pilea of the outer exine (ectexine) supports the pollen wall and prevents mirror buckling. (A) SEM micrograph of the lily pollen exine showing rows of pilea buttressing the wall (scale bar, 5 μm). (B) Schematic representation of the mechanical asymmetry of the buttressed exine. For deformations that make the surface convex, the pilea move apart (middle panel) and are therefore mechanically inactive. For a concave deformation of the exine surface, the pilea are forced against each other (bottom) thus increasing the bending stiffness of the wall.
Similar articles
- Mechanical design of apertures and the infolding of pollen grain.
Božič A, Šiber A. Božič A, et al. Proc Natl Acad Sci U S A. 2020 Oct 27;117(43):26600-26607. doi: 10.1073/pnas.2011084117. Epub 2020 Oct 7. Proc Natl Acad Sci U S A. 2020. PMID: 33028678 Free PMC article. - Light and electron microscopies reveal unknown details of the pollen grain structure and physiology from Brazilian Cerrado species.
Cortez PA, Dos Santos Silva LNN, de Ornellas Paschoalini G, Albuquerque-Pinna J, Sibinelli V, Melo-de-Pinna GFA. Cortez PA, et al. Protoplasma. 2022 Mar;259(2):399-412. doi: 10.1007/s00709-021-01671-9. Epub 2021 Jun 19. Protoplasma. 2022. PMID: 34145472 - Anther development of maize (Zea mays) and longstamen rice (Oryza longistaminata) revealed by cryo-SEM, with foci on locular dehydration and pollen arrangement.
Tsou CH, Cheng PC, Tseng CM, Yen HJ, Fu YL, You TR, Walden DB. Tsou CH, et al. Plant Reprod. 2015 Mar;28(1):47-60. doi: 10.1007/s00497-015-0257-3. Epub 2015 Feb 10. Plant Reprod. 2015. PMID: 25666915 Free PMC article. - Pollen wall development in flowering plants.
Blackmore S, Wortley AH, Skvarla JJ, Rowley JR. Blackmore S, et al. New Phytol. 2007;174(3):483-498. doi: 10.1111/j.1469-8137.2007.02060.x. New Phytol. 2007. PMID: 17447905 Review. - The remarkable biology of pollen.
Bedinger P. Bedinger P. Plant Cell. 1992 Aug;4(8):879-87. doi: 10.1105/tpc.4.8.879. Plant Cell. 1992. PMID: 1392600 Free PMC article. Review. No abstract available.
Cited by
- Magneto-active elastic shells with tunable buckling strength.
Yan D, Pezzulla M, Cruveiller L, Abbasi A, Reis PM. Yan D, et al. Nat Commun. 2021 May 14;12(1):2831. doi: 10.1038/s41467-021-22776-y. Nat Commun. 2021. PMID: 33990557 Free PMC article. - Water status and associated processes mark critical stages in pollen development and functioning.
Firon N, Nepi M, Pacini E. Firon N, et al. Ann Bot. 2012 Jun;109(7):1201-14. doi: 10.1093/aob/mcs070. Epub 2012 Apr 19. Ann Bot. 2012. PMID: 22523424 Free PMC article. Review. - Folded isometric deformations and banana-shaped seedpod.
Couturier E. Couturier E. Proc Math Phys Eng Sci. 2016 Aug;472(2192):20150760. doi: 10.1098/rspa.2015.0760. Proc Math Phys Eng Sci. 2016. PMID: 27616910 Free PMC article. - Systematic palynology in Korean Piperales with special focus on its exine surface ornamentation and orbicule morphology.
Oak MK, Yang S, Choi G, Song JH. Oak MK, et al. Sci Rep. 2022 Mar 9;12(1):4142. doi: 10.1038/s41598-022-08105-3. Sci Rep. 2022. PMID: 35264735 Free PMC article. - The atypically high modulus of pollen exine.
Qu Z, Meredith JC. Qu Z, et al. J R Soc Interface. 2018 Sep 19;15(146):20180533. doi: 10.1098/rsif.2018.0533. J R Soc Interface. 2018. PMID: 30232244 Free PMC article.
References
- Wodehouse RP. Pollen Grains. New York: McGraw-Hill; 1935.
- Heslop-Harrison J. An interpretation of the hydrodynamics of pollen. Am J Bot. 1979;66:737–743.
- Heslop-Harrison J. Pollen walls as adaptive systems. Ann Mo Bot Gard. 1979;66:813–829.
- Thanikaimoni G. Pollen apertures: Form and function. In: Blackmore S, Ferguson IK, editors. Pollen and Spores: Form and Function. London: Academic; 1986. pp. 119–136.
- Payne WW. Observations of harmomegathy in pollen of anthophyta. Grana. 1972;12:93–98.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Molecular Biology Databases