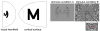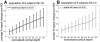Laminar analysis of 7T BOLD using an imposed spatial activation pattern in human V1 - PubMed (original) (raw)
Laminar analysis of 7T BOLD using an imposed spatial activation pattern in human V1
Jonathan R Polimeni et al. Neuroimage. 2010.
Abstract
With sufficient image encoding, high-resolution fMRI studies are limited by the biological point-spread of the hemodynamic signal. The extent of this spread is determined by the local vascular distribution and by the spatial specificity of blood flow regulation, as well as by measurement parameters that (i) alter the relative sensitivity of the acquisition to activation-induced hemodynamic changes and (ii) determine the image contrast as a function of vessel size. In particular, large draining vessels on the cortical surface are a major contributor to both the BOLD signal change and to the spatial bias of the BOLD activation away from the site of neuronal activity. In this work, we introduce a laminar surface-based analysis method and study the relationship between spatial localization and activation strength as a function of laminar depth by acquiring 1mm isotropic, single-shot EPI at 7 T and sampling the BOLD signal exclusively from the superficial, middle, or deep cortical laminae. We show that highly-accelerated EPI can limit image distortions to the point where a boundary-based registration algorithm accurately aligns the EPI data to the surface reconstruction. The spatial spread of the BOLD response tangential to the cortical surface was analyzed as a function of cortical depth using our surface-based analysis. Although sampling near the pial surface provided the highest signal strength, it also introduced the most spatial error. Thus, avoiding surface laminae improved spatial localization by about 40% at a cost of 36% in z-statistic, implying that optimal spatial resolution in functional imaging of the cortex can be achieved using anatomically-informed spatial sampling to avoid large pial vessels.
Copyright 2010 Elsevier Inc. All rights reserved.
Figures
Fig. 1
The resolution stimulus. (A) The letter “M” was warped by the inverse of the known complex-logarithm transformation that describes the topographic mapping of the visual field onto the cortical surface in order to evoke the desired activity pattern on the cortical surface. (B) The visual stimulus as seen by the subjects, consisting of two orthogonal conditions. The inset shows a magnified view of the center of the stimulus, demonstrating the fine spatial noise pattern presented in the center of the visual field.
Fig. 2
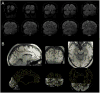
(A) Example EPI slices from a BOLD fMRI scan. (B) Registration of 1-mm isotropic MEMPRAGE anatomical data with EPI data. White matter surface reconstruction is superimposed as yellow contour.
Fig. 3
Laminar analysis of the fMRI activation. (A) Given the cortical surface models, the activation patterns can be projected onto intermediate surfaces lying within the thickness of the cortical gray matter. With small fMRI voxel size, many voxels lie in the central layers of cortex, away from the surface vessels and at the site of highest vascular density. (B) Single axial slice of MEMPRAGE data with the intersections of the family of cortical surface reconstructions overlaid. Each contour represents a single surface at a particular depth; the yellow contour represents the white matter surface, the red contour represents the pial surface. (A collection of 11 surfaces total was used for functional analysis, and only 6 are shown here.) The surface positions are computed from the three-dimensional embedding of the cortical folding pattern, therefore, depending on the angle of intersection between the image plane chosen in this example and the surfaces, in places the contours can appear bunched in this cross section however they are consistently evenly spaced along the cortical thickness in three dimensions. Arrowheads indicate the position of the calcarine sulcus. (C) Magnified view of right calcarine from boxed region in panel (B). The surfaces are most evenly spaced within flat portions of the cortical tissue.
Fig. 4
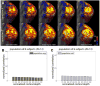
The activity pattern of the “M” stimulus calculated from two 2.5 min. acquisitions (i.e., 5 min. total acquisition time) resulting from differential imaging of the two stimulus conditions, and displayed on the inflated cortical surface. (A) Activity at lowest depth (near white matter). (B-D) Activity at intermediate depths. (E) Activity at shallow depth (near pial surface). Color scale provided on bottom right for _z_-statistic values, which correspond to contrasting the responses from stimulus condition A with responses from stimulus condition B. Activity becomes stronger from the white matter surface the central surfaces, and then deteriorates near the pial surface—consistent with a dominance of the macrovasculature at the pial surface.
Fig. 5
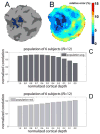
Estimation of spatial spread of activity across cortical depths. (A) Example near-isometric flattening of a patch of the cortical surface with the above-threshold activated vertices labeled, and (B) the corresponding flattening error map. The metric distortion within the activation pattern was on average 3.5% (± 0.7% std.) and everywhere less than 6.8%. (C) The normalized correlation between the desired activity pattern (see Fig. 1) and the measured activity pattern (resulting from contrasting the two stimulus conditions) calculated on the flattened cortical surface across all depths, averaged across all six subjects (i.e., 12 hemispheres). The correlation between the template and the activation pattern decreased consistently with depth, with a 35% increase from the pial surface to the white matter. (D) The standard deviation of the normalized correlation across the population of subjects.
Fig. 6
(A) The percent signal change across depths averaged over all vertices within the V1 ROI. Peak percent signal change appears near the pial surface, in agreement with the larger _z_-statistics seen in Fig. 4 near the surface vessels, despite the lower spatial accuracy. (B) The spatial variance of the response strength quantified as the standard deviation of the percent signal change across depths pooled over all vertices within the V1 ROI. The higher variability of the response strength near the pial surface indicates a larger spatial inhomogeneity nearer to the surface vessels. In both panels, error bars indicate standard deviation across the population of six subjects (12 hemispheres).
Fig. 7
Partial volume effects across depths within a V1 ROI. Average percentage of voxel volume contributed from the three categories: white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF). Only central cortical layers contain gray matter when using 1 mm isotropic voxels. Error bars indicate standard deviation across the population of six subjects (12 hemispheres).
Fig. 8
Functional CNR contributions from gray matter, white matter, and CSF. (A) The relative contributions of the three tissue classes, cortical gray matter, white matter, and surrounding CSF, are plotted against the average _z_-statistic—representing the effect size of the from the differential response—within the predicted boundaries of V1 within one subject. (B) Pooled results of functional CNR measured across the population of six subjects (i.e., 12 hemispheres) with shaded regions indicating population standard deviation. Because absolute _z_-statistic values vary across individuals, the _z_-statistic was linearly mapped to a normalized range for each individual (where 0% represents the minimum _z_-statistic value and 100% represents the maximum _z_-statistic value) prior to averaging across individuals. The slight, relative increase in CSF contribution for the 90% _z_-statistic level is possibly due to partial volume effects across sulci where voxels sample gray matter from opposite sulcal banks.
Fig. 9
Activation maps from single-condition responses. (A) The responses to “stimulus condition A” (top) and “stimulus condition B” (bottom), across several cortical depths. (B) The normalized correlation between the desired activity pattern and the measured single-condition activity pattern, calculated on the flattened cortical surface across all depths, and averaged across all six subjects (i.e., 12 hemispheres). The correlation between the template and the activation pattern did not vary with depth. (C) The standard deviation of the normalized correlation across the population of subjects.
Similar articles
- Improved spatial localization of post-stimulus BOLD undershoot relative to positive BOLD.
Zhao F, Jin T, Wang P, Kim SG. Zhao F, et al. Neuroimage. 2007 Feb 1;34(3):1084-92. doi: 10.1016/j.neuroimage.2006.10.016. Epub 2006 Dec 11. Neuroimage. 2007. PMID: 17161623 Free PMC article. - Resolving laminar activation in human V1 using ultra-high spatial resolution fMRI at 7T.
Kashyap S, Ivanov D, Havlicek M, Sengupta S, Poser BA, Uludağ K. Kashyap S, et al. Sci Rep. 2018 Nov 20;8(1):17063. doi: 10.1038/s41598-018-35333-3. Sci Rep. 2018. PMID: 30459391 Free PMC article. - Layer-specific BOLD activation in awake monkey V1 revealed by ultra-high spatial resolution functional magnetic resonance imaging.
Chen G, Wang F, Gore JC, Roe AW. Chen G, et al. Neuroimage. 2013 Jan 1;64:147-55. doi: 10.1016/j.neuroimage.2012.08.060. Epub 2012 Aug 28. Neuroimage. 2013. PMID: 22960152 Free PMC article. - Human cortical areas underlying the perception of optic flow: brain imaging studies.
Greenlee MW. Greenlee MW. Int Rev Neurobiol. 2000;44:269-92. doi: 10.1016/s0074-7742(08)60746-1. Int Rev Neurobiol. 2000. PMID: 10605650 Review. - Laminar fMRI: What can the time domain tell us?
Petridou N, Siero JCW. Petridou N, et al. Neuroimage. 2019 Aug 15;197:761-771. doi: 10.1016/j.neuroimage.2017.07.040. Epub 2017 Jul 20. Neuroimage. 2019. PMID: 28736308 Free PMC article. Review.
Cited by
- Interdigitated Columnar Representation of Personal Space and Visual Space in Human Parietal Cortex.
Tootell RBH, Nasiriavanaki Z, Babadi B, Greve DN, Nasr S, Holt DJ. Tootell RBH, et al. J Neurosci. 2022 Nov 30;42(48):9011-9029. doi: 10.1523/JNEUROSCI.0516-22.2022. Epub 2022 Oct 5. J Neurosci. 2022. PMID: 36198501 Free PMC article. - Intracortical depth analyses of frequency-sensitive regions of human auditory cortex using 7TfMRI.
Ahveninen J, Chang WT, Huang S, Keil B, Kopco N, Rossi S, Bonmassar G, Witzel T, Polimeni JR. Ahveninen J, et al. Neuroimage. 2016 Dec;143:116-127. doi: 10.1016/j.neuroimage.2016.09.010. Epub 2016 Sep 5. Neuroimage. 2016. PMID: 27608603 Free PMC article. - High-field FMRI for human applications: an overview of spatial resolution and signal specificity.
Olman CA, Yacoub E. Olman CA, et al. Open Neuroimag J. 2011;5:74-89. doi: 10.2174/1874440001105010074. Epub 2011 Nov 4. Open Neuroimag J. 2011. PMID: 22216080 Free PMC article. - Ultra-high-resolution fMRI of Human Ventral Temporal Cortex Reveals Differential Representation of Categories and Domains.
Margalit E, Jamison KW, Weiner KS, Vizioli L, Zhang RY, Kay KN, Grill-Spector K. Margalit E, et al. J Neurosci. 2020 Apr 8;40(15):3008-3024. doi: 10.1523/JNEUROSCI.2106-19.2020. Epub 2020 Feb 24. J Neurosci. 2020. PMID: 32094202 Free PMC article. - Interdigitated Color- and Disparity-Selective Columns within Human Visual Cortical Areas V2 and V3.
Nasr S, Polimeni JR, Tootell RB. Nasr S, et al. J Neurosci. 2016 Feb 10;36(6):1841-57. doi: 10.1523/JNEUROSCI.3518-15.2016. J Neurosci. 2016. PMID: 26865609 Free PMC article.
References
- Annese J, Pitiot A, Dinov ID, Toga AW. A myeloarchitectonic method for the structural classification of cortical areas. NeuroImage. 2004;21(1):15–26. - PubMed
- Bandettini PA, Wong EC, Jesmanowicz A, Hinks RS, Hyde JS. Spin-echo and gradient-echo EPI of human brain activation using BOLD contrast: a comparative study at 1.5 T. NMR Biomed. 1994;7(1–2):12–20. - PubMed
- Barth M, Norris DG. Very high-resolution three-dimensional functional MRI of the human visual cortex with elimination of large venous vessels. NMR Biomed. 2007;20(5):477–84. - PubMed
- Blinkov SM, Glezer II. The Human Brain in Figures and Tables. Basic Books, Inc., Plenum Press; New York: 1968.
Publication types
MeSH terms
Grants and funding
- R01 AG018386/AG/NIA NIH HHS/United States
- AG02238/AG/NIA NIH HHS/United States
- P41 RR014075/RR/NCRR NIH HHS/United States
- R01 NS052585/NS/NINDS NIH HHS/United States
- R01 EB006847/EB/NIBIB NIH HHS/United States
- R01 EB006758/EB/NIBIB NIH HHS/United States
- R01 AG022381/AG/NIA NIH HHS/United States
- P41 RR14075/RR/NCRR NIH HHS/United States
- R01 NS052585-01/NS/NINDS NIH HHS/United States
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical