Learning task-optimal registration cost functions for localizing cytoarchitecture and function in the cerebral cortex - PubMed (original) (raw)
Learning task-optimal registration cost functions for localizing cytoarchitecture and function in the cerebral cortex
B T Thomas Yeo et al. IEEE Trans Med Imaging. 2010 Jul.
Abstract
Image registration is typically formulated as an optimization problem with multiple tunable, manually set parameters. We present a principled framework for learning thousands of parameters of registration cost functions, such as a spatially-varying tradeoff between the image dissimilarity and regularization terms. Our approach belongs to the classic machine learning framework of model selection by optimization of cross-validation error. This second layer of optimization of cross-validation error over and above registration selects parameters in the registration cost function that result in good registration as measured by the performance of the specific application in a training data set. Much research effort has been devoted to developing generic registration algorithms, which are then specialized to particular imaging modalities, particular imaging targets and particular postregistration analyses. Our framework allows for a systematic adaptation of generic registration cost functions to specific applications by learning the "free" parameters in the cost functions. Here, we consider the application of localizing underlying cytoarchitecture and functional regions in the cerebral cortex by alignment of cortical folding. Most previous work assumes that perfectly registering the macro-anatomy also perfectly aligns the underlying cortical function even though macro-anatomy does not completely predict brain function. In contrast, we learn 1) optimal weights on different cortical folds or 2) optimal cortical folding template in the generic weighted sum of squared differences dissimilarity measure for the localization task. We demonstrate state-of-the-art localization results in both histological and functional magnetic resonance imaging data sets.
Figures
Fig. 1
Traditional and proposed frameworks for image registration.{In} indicates a collection of images. In image registration, we seek a deformation Γn* for each image In. The resulting deformations {Γn*} are then used for other applications, such as segmentation or group analysis. The registration cost function typically contains multiple parameters, such as the tradeoff parameter λ and the template T. Changes in these parameters alter the deformations {Γn*} and thus the outcomes of downstream applications. In our framework (b), we assume a training data set, which allows us to evaluate the quality of the registration as measured by the application performance (or cross-validation error metric) gn for each training subject. This allows us to pick the best parameters that result in good registration as measured by {gn}. Subsequent new subjects are registered using these learned parameters.
Fig. 2
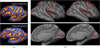
Examples of ambiguities in image registration, which can potentially be resolved by taking the application at hand into account. (a) Postcentral sulci with different topology. (b) BAs overlaid on cortical surfaces.
Fig. 3
Illustration of the differences between our approach and the pairwise registration approach. In our approach, we use training images and labels to learn an optimal cost function that is optimal for aligning the labels of the training and template subjects. This cost function is then used to register and predict the hidden label in a new subject. (a) Pairwise registration without training using ground truth labels. (b) Task-optimal registration framework.
Fig. 4
FreeSurfer’s atlas-based registration approach. Training and test subjects are registered to an atlas. The BA of a training subject can then be used to predict that of the test subject.
Fig. 5
Mean Hausdorff distances over an entire range of harmonic energy for BA44, BA45, and MT. First row corresponds to left hemisphere. Second row corresponds to right hemipshere. * indicates that task-optimal template is statistically significantly better than FreeSurfer. † indicates that task-optimal weights is statistically significantly better than FreeSurfer. Statistical threshold is set at 0.05, FDR corrected with respect to the 24 statistical tests performed in this section. FreeSurfer is not statistically better than either of the task-optimal methods in any of the Brodmann areas. (a) Left BA44 *, †. (b) Left BA45 *, †. (c) Left MT. (d) Right BA44 *. (e) Right BA45 *, †. (f) Right MT*, †.
Fig. 6
Mean Hausdorff distances over an entire range of harmonic energy for V1, V2, and BA2. First row corresponds to left hemisphere. Second row corresponds to right hemisphere. * indicates that task-optimal template is statistically significantly better than FreeSurfer. † indicates that task-optimal weights is statistically significantly better than FreeSurfer. Statistical threshold is set at 0.05, FDR corrected with respect to the 24 statistical tests performed in this section. FreeSurfer is not statistically better than either of the task-optimal methods in any of the Brodmann areas. (a) Left V1 *. (b) Left V2 *, †. (c) Left BA2 *, †. (d) Right V1 *. (e) Right V2 *, †. (f) Right BA2.
Fig. 7
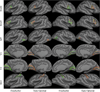
Representative BA localization in 90 trials of leave-two-out for FreeSurfer and task-optimal template. Yellow indicates ground truth boundary. Green indicates FreeSurfer prediction. Red indicates Task-Optimal prediction. The representative samples were selected by finding subjects whose localization errors are close to the mean localization errors for each BA. Furthermore, for a given BA, the same subject was selected for both methods to simplify the comparison.
Fig. 8
Template estimation in the task-optimal framework improves localization of BA2. (a) Cortical geometry of test subject with corresponding BA2 (in green). (b) Initial cortical geometry of template subject with corresponding BA2 (in black). In (b), we also show the BA2 of the test subject (in green) after registration to the intial template. (c) Final cortical geometry of template subject after task-optimal training. BA2 of the test subject (in green) after registration to the task-optimal template demonstrates significantly better alignment with the BA2 of the template subject.
Fig. 9
Mean Hausdorff distances using ex vivo MT to predict MT+ in in vivo scans. Permutation testing shows that the differences between FreeSurfer and task-optimal template are statistically significant (p < 10−5).
Fig. 10
Plot of mean hausdorff errors for MT+ from cross-validation of the fMRI data set using either FreeSurfer or in vivo trained task-optimal template. For the task-optimal framework, we tried different number of training subjects. Test errors decrease as we go from 9 to 19 to 29 training subjects. Once again, permutation testing shows that the differences between FreeSurfer and task-optimal template are statistically significant (p < 10−5).
Similar articles
- Task-optimal registration cost functions.
Yeo BT, Sabuncu M, Golland P, Fischl B. Yeo BT, et al. Med Image Comput Comput Assist Interv. 2009;12(Pt 1):598-606. doi: 10.1007/978-3-642-04268-3_74. Med Image Comput Comput Assist Interv. 2009. PMID: 20426037 Free PMC article. - Simultaneous registration and segmentation of anatomical structures from brain MRI.
Wang F, Vemuri BC. Wang F, et al. Med Image Comput Comput Assist Interv. 2005;8(Pt 1):17-25. doi: 10.1007/11566465_3. Med Image Comput Comput Assist Interv. 2005. PMID: 16685824 - Multimodal surface matching: fast and generalisable cortical registration using discrete optimisation.
Robinson EC, Jbabdi S, Andersson J, Smith S, Glasser MF, Van Essen DC, Burgess G, Harms MP, Barch DM, Barch DM. Robinson EC, et al. Inf Process Med Imaging. 2013;23:475-86. doi: 10.1007/978-3-642-38868-2_40. Inf Process Med Imaging. 2013. PMID: 24683992 - Topology-preserving tissue classification of magnetic resonance brain images.
Bazin PL, Pham DL. Bazin PL, et al. IEEE Trans Med Imaging. 2007 Apr;26(4):487-96. doi: 10.1109/TMI.2007.893283. IEEE Trans Med Imaging. 2007. PMID: 17427736 - Brain functional localization: a survey of image registration techniques.
Gholipour A, Kehtarnavaz N, Briggs R, Devous M, Gopinath K. Gholipour A, et al. IEEE Trans Med Imaging. 2007 Apr;26(4):427-51. doi: 10.1109/TMI.2007.892508. IEEE Trans Med Imaging. 2007. PMID: 17427731 Review.
Cited by
- Individual-Specific Areal-Level Parcellations Improve Functional Connectivity Prediction of Behavior.
Kong R, Yang Q, Gordon E, Xue A, Yan X, Orban C, Zuo XN, Spreng N, Ge T, Holmes A, Eickhoff S, Yeo BTT. Kong R, et al. Cereb Cortex. 2021 Aug 26;31(10):4477-4500. doi: 10.1093/cercor/bhab101. Cereb Cortex. 2021. PMID: 33942058 Free PMC article. - Accurate nonlinear mapping between MNI volumetric and FreeSurfer surface coordinate systems.
Wu J, Ngo GH, Greve D, Li J, He T, Fischl B, Eickhoff SB, Yeo BTT. Wu J, et al. Hum Brain Mapp. 2018 Sep;39(9):3793-3808. doi: 10.1002/hbm.24213. Epub 2018 May 16. Hum Brain Mapp. 2018. PMID: 29770530 Free PMC article. - Analysis strategies for high-resolution UHF-fMRI data.
Polimeni JR, Renvall V, Zaretskaya N, Fischl B. Polimeni JR, et al. Neuroimage. 2018 Mar;168:296-320. doi: 10.1016/j.neuroimage.2017.04.053. Epub 2017 Apr 29. Neuroimage. 2018. PMID: 28461062 Free PMC article. Review. - Reducing Individual Variation for fMRI Studies in Children by Minimizing Template Related Errors.
Weng J, Dong S, He H, Chen F, Peng X. Weng J, et al. PLoS One. 2015 Jul 24;10(7):e0134195. doi: 10.1371/journal.pone.0134195. eCollection 2015. PLoS One. 2015. PMID: 26207985 Free PMC article. - Multi-atlas segmentation of biomedical images: A survey.
Iglesias JE, Sabuncu MR. Iglesias JE, et al. Med Image Anal. 2015 Aug;24(1):205-219. doi: 10.1016/j.media.2015.06.012. Epub 2015 Jul 6. Med Image Anal. 2015. PMID: 26201875 Free PMC article. Review.
References
- Allassonniere S, Amit Y, Trouvé A. Toward a coherent statistical framework for dense deformable template estimation. J. R. Stat. Soc., Series B. 2007;vol. 69(no. 1):3–29.
- Allgower E, Georg K. Introduction to Numerical Continuation Methods. Philadelphia, PA: SIAM; 2003.
- Amunts K, Malikovic A, Mohlberg H, Schormann T, Zilles K. Brodmann’s areas 17 and 18 brought into stereotaxic space—Where and how variable? NeuroImage. 2000;vol. 11:66–84. - PubMed
- Amunts K, Schleicher A, Burgel U, Mohlberg H, Uylings H, Zilles K. Broca’s region revisited: Cytoarchitecture and intersubject variability. J. Comparative Neurol. 1999;vol. 412(no. 2):319–341. - PubMed
- Arsigny V, Commowick O, Pennec X, Ayache N. A log-euclidean framework for statistics on diffeomorphisms. Proc. Int. Conf. Med. Image Computing Computer Assist. Intervent. (MICCAI); LNCS; 2006. pp. 924–931. - PubMed
Publication types
MeSH terms
Grants and funding
- U24 RR021382/RR/NCRR NIH HHS/United States
- R01EB001550/EB/NIBIB NIH HHS/United States
- P41-RR13218/RR/NCRR NIH HHS/United States
- R01EB006758/EB/NIBIB NIH HHS/United States
- R01-NS051826/NS/NINDS NIH HHS/United States
- R01 NS052585-01/NS/NINDS NIH HHS/United States
- AG02238/AG/NIA NIH HHS/United States
- R01 EB001550/EB/NIBIB NIH HHS/United States
- U54 EB005149/EB/NIBIB NIH HHS/United States
- R01 NS052585/NS/NINDS NIH HHS/United States
- P41 RR013218/RR/NCRR NIH HHS/United States
- R01 RR16594-01A1/RR/NCRR NIH HHS/United States
- U24-RR021382/RR/NCRR NIH HHS/United States
- R01 RR016594/RR/NCRR NIH HHS/United States
- R01 EB006758/EB/NIBIB NIH HHS/United States
- R01 AG022381/AG/NIA NIH HHS/United States
- P41-RR14075/RR/NCRR NIH HHS/United States
- K25 EB013649/EB/NIBIB NIH HHS/United States
- U54-EB005149/EB/NIBIB NIH HHS/United States
- P41 RR014075/RR/NCRR NIH HHS/United States
- R01 NS051826/NS/NINDS NIH HHS/United States
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical