Optimal matrix rigidity for stress fiber polarization in stem cells - PubMed (original) (raw)

Optimal matrix rigidity for stress fiber polarization in stem cells

A Zemel et al. Nat Phys. 2010.

Abstract

The shape and differentiation of human mesenchymal stem cells is especially sensitive to the rigidity of their environment; the physical mechanisms involved are unknown. A theoretical model and experiments demonstrate here that the polarization/alignment of stress-fibers within stem cells is a non-monotonic function of matrix rigidity. We treat the cell as an active elastic inclusion in a surrounding matrix whose polarizability, unlike dead matter, depends on the feedback of cellular forces that develop in response to matrix stresses. The theory correctly predicts the monotonic increase of the cellular forces with the matrix rigidity and the alignment of stress-fibers parallel to the long axis of cells. We show that the anisotropy of this alignment depends non-monotonically on matrix rigidity and demonstrate it experimentally by quantifying the orientational distribution of stress-fibers in stem cells. These findings offer a first physical insight for the dependence of stem cell differentiation on tissue elasticity.

PubMed Disclaimer

Figures

Figure 1

Figure 1

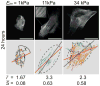
Acto-myosin stress-fiber alignment in hMSCs sparsely plated on 2D substrates of different elasticity. The top row shows hMSCs immuno-stained for non-muscle myosin IIa (NMMIIa) 24 hours after plating on elastic substrates with a Young’s modulus Em of 1 kPa, 11 kPa, and 34 kPa that are the most representative cells of the mean values obtained for cell area A, aspect ratio of long to short axis r, and stress-fiber order parameter S = 〈_cos_2_θ_〉; where θ is the angle between each stress-fiber in the cell and the long axis of the fitted ellipse. The bottom row shows the respective orientational plots, where the different orientations of myosin filaments are depicted with different colours. The dark gray dashed ellipses are best fits to the cell edge and the red line indicates the mean orientation of the stress-fibers as determined by the automated algorithm. ξ is the angle between the mean stress-fiber orientation and the principal axis of the ellipse. From symmetry considerations we need only consider the absolute value of ξ between 0 and _π/_2; thus, a completely random distribution has an average ξ = _π/_4. Values given for r and S are the mean values of at least 60 cells per condition. All scale bars represent 50 _μ_m.

Figure 2

Figure 2

Cell adhesion and polarization represented by a 1D spring model. Springs with constants kc and km represent the elasticity of the cell and matrix respectively. Elastic morphological changes upon cell adhesion (a → b) are represented here by a change in the cellular spring length −Δlc0=lc0−lcR>0. This triggers an internal feedback mechanism (b→c) that results in an enhancement of the active forces (see Eq. 2).

Figure 3

Figure 3

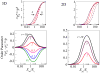
Cell polarization as a function of the ratio of the Young’s modulus of the matrix, Em, and the cell, Ec, in both our two- and three-dimensional models; the plots are shown for different values of the cellular aspect ratio, r. The upper panels show (magenta: r = 5, red: r = 2) the normalized average dipole elements 〈pzza〉 (solid lines) and 〈pxxa〉 (dashed lines) corresponding to the forces in the directions that are respectively parallel (ẑ) and perpendicular (x̂) to the long axis of the cell. The bottom panels show the calculated orientational order parameter of the stress-fibers that is given by the normalized difference (〈pzza〉−〈pxxa〉)/p. The color coding indicates the aspect ratio. In this plot the Poisson ratio of the matrix and the cellular domain are taken to be, νm = 0.45, νc = 0.3 and the magnitude of the polarizability is α = 3.

Figure 4

Figure 4

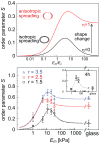
The effect of axial cell elongation on stress-fiber polarization and experimental values of the order parameter S for different elastic substrates. Upper panel shows a calculation of the 2D order parameter as a function of the matrix rigidity, for two cases: (i) (black curve) the cell spreads isotropically on the substrate, η = 0, and (ii) (red curve) the cell spreads anisotropically on the substrate, η = 1, see text. The two illustrations left of the curves show top views over the cell, before (shown as blank) and after (shown as shaded) cell spreading. In the asymmetric spreading case, r corresponds to the cell shape in an infinitely rigid matrix. For both curves we used r = 2, α = 2 and Poisson ratios as in Fig. 3. The bottom panel shows the experimental values of the stress-fiber order parameter, S = 〈_cos_2_θ_〉, 24 hours after plating the cells, for the three groups of cells (of aspect ratios r = 1.5, 2.5, 3.5) as a function of the Young’s modulus of the matrix, Em; θ is the angle between each stress-fiber in the cell and the long axis of the fitted ellipse. Within each of the different groups, S is maximal for Em = 11 kPa and generally increases with aspect ratio r, in agreement with our theoretical predictions. Error bars denote the standard error of the mean and theory curves (dotted lines) calculated from the simplified expansion of S (supporting Information) are shown to guide the eye.

Similar articles

Cited by

References

    1. O’Neill C, Jordan P, Ireland G. Evidence for two distinct mechanisms of anchorage stimulation in freshly explanted and 3t3 swiss mouse fibroblasts. Cell. 1986;44:489–496. - PubMed
    1. Chen CS, Mrksich M, Huang S, Whitesides GM, Ingber DE. Geometric control of cell life and death. Science. 1997;276:1425–1428. - PubMed
    1. McBeath R, Pirone DM, Nelson CM, Bhadriraju K, Chen CS. Cell shape, cytoskeleton tension, and RohA regulate stem cell lineage commitment. Developmental Cell. 2004;6:483–495. - PubMed
    1. Engler AJ, et al. Myotubes differentiate optimally on substrates with tissue-like stiffness: pathological implications for soft or stiff microenvironments. J Cell Biol. 2004;166:877–887. - PMC - PubMed
    1. Yeung T, et al. Effects of substrate stiffness on cell morphology, cytoskeletal structure, and adhesion. Cell Motil Cytoskeleton. 2005;60:24–34. - PubMed

Grants and funding

LinkOut - more resources