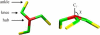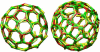Asymmetry as the key to clathrin cage assembly - PubMed (original) (raw)
Asymmetry as the key to clathrin cage assembly
Wouter K den Otter et al. Biophys J. 2010.
Abstract
The self-assembly of clathrin proteins into polyhedral cages is simulated for the first time (to our knowledge) by introducing a coarse-grain triskelion particle modeled after clathrin's characteristic shape. The simulations indicate that neither this shape, nor the antiparallel binding of four legs along the lattice edges, is sufficient to induce cage formation from a random solution. Asymmetric intersegmental interactions, which probably result from a patchy distribution of interactions along the legs' surfaces, prove to be crucial for the efficient self-assembly of cages.
2010 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures
Figure 1
The triskelion simulation model, shown here in top view (left) and side view (right), is based on the idealized structure of clathrin. Three proximal legs run from the central hub (red) to a knee (green), under a pucker angle χ relative to the threefold rotational symmetry axis (_C_3), followed by three distal legs running from the knees to the ankles (yellow). In all simulations, the pucker angle was set equal to 101°. The particle is simulated as a rigid unit with proximal and distal legs of equal length.
Figure 2
Triskelia of the first simulation model, at segmental binding energies ε = 7 k_B_T (A) and ε = 8 k_B_T (B), have a tendency to self-assemble into chainlike structures. The number of branch points increases with the segmental binding energy, and thereby changes the shape of the aggregates.
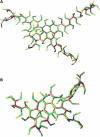
Figure 3
Experimentally resolved structure of a lattice edge in a hexagonal barrel viewed (A) from the top, (B) from the side, and (C) in cross section. The two antiparallel proximal leg-segments (red and green) are in the front of the top view and on top in the side view and cross section, the two antiparallel distal leg-segments (blue and amber) are in the back of the top view and at the bottom of the side view and cross section. Proximal and distal legs are similar in structure and are clearly asymmetric, with two faces made of _α_-helices and two faces made of connecting loops. A gradual right-handed twist along the leg has rotated the elliptic cross sections of the distal legs by ∼90° relative to those of the proximal legs. The cartoons in Figs. 4 and 7 are based on this structure. (Reproduced with permission from the authors and Macmillan Publishers from the supplementary material to Fotin et al. (8).)
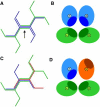
Figure 4
Schematic of the probable edge structure in a clathrin cage, based on the experimental structure (5–8) provided in Fig. 3. An edge (marked by an arrow in panel A) combines two antiparallel proximal legs (dark blue) of the two clathrins centered at the flanking vertices with two antiparallel distal legs (light green) of two clathrins centered at next-nearest vertices. In the cross section (B), the hub-to-knee and knee-to-ankle directions are indicated by the symbols ⊙ and ⊗ for segments pointing out of and into the paper, respectively. The diagram illustrates that the asymmetric segments are preferentially oriented with the shaded regions (schematically representing the segmental interactions) oriented toward the center of the edge. Rotating the upper-right dark blue clathrin by 180° around the direction of the marked edge yields the upside-down red clathrin (C), whose poor binding is explained in cross section (D) by a mismatch of the shaded areas. The latter configuration is very common, however, in the simulations with the nondirectional model, where it gives rise to the typical stringlike structures of Fig. 2 with alternating up-down orientations for consecutive pairs of particles.
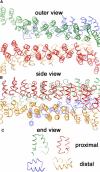
Figure 5
Snapshots after ∼5,000,000 Monte Carlo trial moves per particle, starting from a random initial configuration, for the interaction models with nonpatchy (A) and patchy (B) segmental interactions at a segmental interaction energy of ε = 8 k_B_T. Whereas the model with nondirectional interactions yields chainlike aggregates of various shapes (two isolated clusters are shown in Fig. 2), the model with directional interactions readily self-assembles into near-spherical cages of fairly uniform size (two isolated cages are shown in Fig. 6). The actual simulation boxes are approximately four times as large, containing 104 particles at a density of 10−3_σ_−3 corresponding to the critical assembly concentration of ∼100 _μ_g/ml.
Figure 6
Two typical self-assembled cages grown at ε = 8 k_B_T with the patchy model. Closed polyhedral cages formed by triskelia with a pucker χ = 101° contain ∼60–70 particles, forming exactly 12 pentagonal faces and ∼20 hexagonal faces. The cage on the left is rotated to create a coalescence of the edges in the front with those in the rear.
Figure 7
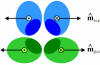
Cross section of a cage edge showing the preferred orientations of the m^-vectors for maximum binding between the leg segments. The two proximal-proximal m^-vectors are antiparallel, as are the two distal-distal m^-vectors, whereas combinations of a proximal and a distal segment can yield both parallel and antiparallel m^-vectors depending on the segments involved.
Similar articles
- Self-assembly of three-legged patchy particles into polyhedral cages.
den Otter WK, Renes MR, Briels WJ. den Otter WK, et al. J Phys Condens Matter. 2010 Mar 17;22(10):104103. doi: 10.1088/0953-8984/22/10/104103. Epub 2010 Feb 23. J Phys Condens Matter. 2010. PMID: 21389437 - Clathrin Assembly Regulated by Adaptor Proteins in Coarse-Grained Models.
Giani M, den Otter WK, Briels WJ. Giani M, et al. Biophys J. 2016 Jul 12;111(1):222-35. doi: 10.1016/j.bpj.2016.06.003. Biophys J. 2016. PMID: 27410749 Free PMC article. - Rotational Brownian dynamics simulations of clathrin cage formation.
Ilie IM, den Otter WK, Briels WJ. Ilie IM, et al. J Chem Phys. 2014 Aug 14;141(6):065101. doi: 10.1063/1.4891306. J Chem Phys. 2014. PMID: 25134598 - Structure and Assembly of Clathrin Cages.
Halebian M, Morris K, Smith C. Halebian M, et al. Subcell Biochem. 2017;83:551-567. doi: 10.1007/978-3-319-46503-6_20. Subcell Biochem. 2017. PMID: 28271490 Review. - Clathrin's life beyond 40: Connecting biochemistry with physiology and disease.
Briant K, Redlingshöfer L, Brodsky FM. Briant K, et al. Curr Opin Cell Biol. 2020 Aug;65:141-149. doi: 10.1016/j.ceb.2020.06.004. Epub 2020 Aug 21. Curr Opin Cell Biol. 2020. PMID: 32836101 Review.
Cited by
- Unraveling protein-protein interactions in clathrin assemblies via atomic force spectroscopy.
Jin AJ, Lafer EM, Peng JQ, Smith PD, Nossal R. Jin AJ, et al. Methods. 2013 Mar;59(3):316-27. doi: 10.1016/j.ymeth.2012.12.006. Epub 2012 Dec 25. Methods. 2013. PMID: 23270814 Free PMC article. - Large self-assembled clathrin lattices spontaneously disassemble without sufficient adaptor proteins.
Guo SK, Sodt AJ, Johnson ME. Guo SK, et al. PLoS Comput Biol. 2022 Mar 21;18(3):e1009969. doi: 10.1371/journal.pcbi.1009969. eCollection 2022 Mar. PLoS Comput Biol. 2022. PMID: 35312692 Free PMC article. - DNA-Origami-Based Fluorescence Brightness Standards for Convenient and Fast Protein Counting in Live Cells.
Williams ND, Landajuela A, Kasula RK, Zhou W, Powell JT, Xi Z, Isaacs FJ, Berro J, Toomre D, Karatekin E, Lin C. Williams ND, et al. Nano Lett. 2020 Dec 9;20(12):8890-8896. doi: 10.1021/acs.nanolett.0c03925. Epub 2020 Nov 9. Nano Lett. 2020. PMID: 33164530 Free PMC article. - Micellization model for the polymerization of clathrin baskets.
Muthukumar M, Nossal R. Muthukumar M, et al. J Chem Phys. 2013 Sep 28;139(12):121928. doi: 10.1063/1.4816634. J Chem Phys. 2013. PMID: 24089740 Free PMC article. - Membrane fluctuations destabilize clathrin protein lattice order.
Cordella N, Lampo TJ, Mehraeen S, Spakowitz AJ. Cordella N, et al. Biophys J. 2014 Apr 1;106(7):1476-88. doi: 10.1016/j.bpj.2013.11.4505. Biophys J. 2014. PMID: 24703309 Free PMC article.
References
- Edeling M.A., Smith C., Owen D. Life of a clathrin coat: insights from clathrin and AP structures. Nat. Rev. Mol. Cell Biol. 2006;7:32–44. - PubMed
- Young A. Structural insights into the clathrin coat. Semin. Cell Dev. Biol. 2007;18:448–458. - PubMed
- Ungewickell E.J., Hinrichsen L. Endocytosis: clathrin-mediated membrane budding. Curr. Opin. Cell Biol. 2007;19:417–425. - PubMed
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources