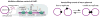Fundamental limits on the suppression of molecular fluctuations - PubMed (original) (raw)

Fundamental limits on the suppression of molecular fluctuations

Ioannis Lestas et al. Nature. 2010.

Abstract

Negative feedback is common in biological processes and can increase a system's stability to internal and external perturbations. But at the molecular level, control loops always involve signalling steps with finite rates for random births and deaths of individual molecules. Here we show, by developing mathematical tools that merge control and information theory with physical chemistry, that seemingly mild constraints on these rates place severe limits on the ability to suppress molecular fluctuations. Specifically, the minimum standard deviation in abundances decreases with the quartic root of the number of signalling events, making it extremely expensive to increase accuracy. Our results are formulated in terms of experimental observables, and existing data show that cells use brute force when noise suppression is essential; for example, regulatory genes are transcribed tens of thousands of times per cell cycle. The theory challenges conventional beliefs about biochemical accuracy and presents an approach to the rigorous analysis of poorly characterized biological systems.

PubMed Disclaimer

Figures

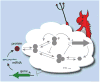
Figure 1

Figure 1. Schematic of optimal control networks and information loss

Biological networks can be overwhelmingly complex, with numerous feedback loops and signaling steps. Predictions about noise then rely on quantitative estimates for how every probabilistic reaction rate responds to every type of perturbation. To investigate bounds on behavior, most of the network is here replaced by a ‘control demon’ representing a controller that is optimized over all possible network topologies, rates and mechanisms. The bounds are then calculated in terms of the few specified features.

Figure 2

Figure 2. Hard limits on standard deviations

(left) Intrinsic noise (Eq. (1)). The lower limit on the relative standard deviation normalized by that of a Poisson distribution, as a function of the ratio _N_2/_N_1. Blue curve corresponds to reaction scheme (1), and red to the autocatalytic scheme described above Eq. (5). The quartic root is the strongest relative response along either curve, while at low relative signaling frequencies the limit is an even more damped function of _N_2/_N_1. (Left, inset) The same lower limit for an average of 100 X1 molecules, as a function of _N_2. (Right) Extrinsic noise. X1 is made at rate x_3_u, where X3 is born with constant probability and decays exponentially with rate 1/_τ_3, while intrinsic birth and death noise in X1 is ignored. For _τ_3≪_τ_1 or _τ_3≫_τ_1, the quartic root asymptotic still applies, essentially because the process mimics a one-variable random process in both cases. At intermediate time-scales the _N_2 dependence is less strict and _τ_3=_τ_1 produces an asymptotic power law exponent of 3/8 rather than ¼, partly supporting previous, conclusions that extrinsic noise is slightly easier to suppress. However, many actual control systems may find intermediately slow noise the hardest to eliminate and any predictions about suppressing extrinsic noise will depend on the properties of that noise. The predicted extrinsic noise limit is also a conservative estimate, and the actual magnitude of the noise limit may be slightly higher (SI).

Figure 3

Figure 3. Plasmid replication control

(Left) Plasmid ColE1 expresses an inhibitor that prevents replication, similarly to the self-replication model in the main text with X1 as plasmid and X2 as inhibitor. Because plasmids are under selection for noise suppression the theory predicts it must maximize expression rates and minimize the length of signaling cascades while still achieving ‘cooperative’ nonlinear effects in the control loop. ColE1 indeed expresses a short-lived anti-sense RNA inhibitor (RNA I) tens of thousands of times per cell cycle (~10Hz), that directly and irreversibly blocks the maturation of a constitutively synthesized sense-RNA replication pre-primer (RNA II) – eliminating both the translation step and binding and unbinding to genes and making it energetically and mechanistically possible to produce inhibitors at such high rates. ColE1 could also create strongly nonlinear control kinetics by exploiting kinetic proofreading in RNA II elongation,. Many unrelated plasmids similarly express anti-sense inhibitors at high rates, avoid cascades, and use multistep inhibition kinetics. (Right) Plasmids such as P1, F, and pSC101 use ‘handcuffing’ mechanisms, where repeated DNA sequences (iterons) bind each other and prevent replication. This can achieve similar homeostatic dynamics as monomer-dimer equilibria where a higher fraction of molecules are in dimer form at higher abundance. Using DNA itself as inhibitor this could eliminate the need for indirect signaling altogether, but because the mechanisms seem incapable of strongly nonlinear corrections, most such plasmids use additional control systems that go through gene expression and thus are subject to information loss. Plasmids also commonly use counteracting loops, where replication inhibitors also auto-inhibit their own synthesis – a counter-intuitive strategy that in fact can improve control greatly (increasing _H_22 for a given high _H_21 in Eq. (4)).

Comment in

Similar articles

Cited by

References

    1. Ozbudak EM, Thattai M, Kurtser I, Grossman AD, van Oudenaarden A. Regulation of noise in the expression of a single gene. Nature Genetics. 2002;31:69–73. - PubMed
    1. Elowitz MB, Levine AJ, Siggia ED, Swain PS. Stochastic gene expression in a single cell. Science (Washington, DC, United States) 2002;297:1183–1186. - PubMed
    1. Newman JR, et al. Single-cell proteomic analysis of S. cerevisiae reveals the architecture of biological noise. Nature. 2006;441:840–846. - PubMed
    1. Golding I, Paulsson J, Zawilski SM, Cox EC. Real-time kinetics of gene activity in individual bacteria. Cell (Cambridge, MA, United States) 2005;123:1025–1036. - PubMed
    1. Paulsson J, Ehrenberg M. Noise in a minimal regulatory network: Plasmid copy number control. Quarterly Reviews of Biophysics. 2001;34:1–59. - PubMed

Publication types

MeSH terms

Grants and funding

LinkOut - more resources