Analysis of population structure: a unifying framework and novel methods based on sparse factor analysis - PubMed (original) (raw)
Analysis of population structure: a unifying framework and novel methods based on sparse factor analysis
Barbara E Engelhardt et al. PLoS Genet. 2010.
Abstract
We consider the statistical analysis of population structure using genetic data. We show how the two most widely used approaches to modeling population structure, admixture-based models and principal components analysis (PCA), can be viewed within a single unifying framework of matrix factorization. Specifically, they can both be interpreted as approximating an observed genotype matrix by a product of two lower-rank matrices, but with different constraints or prior distributions on these lower-rank matrices. This opens the door to a large range of possible approaches to analyzing population structure, by considering other constraints or priors. In this paper, we introduce one such novel approach, based on sparse factor analysis (SFA). We investigate the effects of the different types of constraint in several real and simulated data sets. We find that SFA produces similar results to admixture-based models when the samples are descended from a few well-differentiated ancestral populations and can recapitulate the results of PCA when the population structure is more "continuous," as in isolation-by-distance models.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
Figure 1. Low-dimensional matrix factorization via factor analysis.
Each matrix in Equation 1 is illustrated by a blue rectangle and labeled. As in Equation 2, a single element of genotype matrix  ,
,  is shown in red, and is computed from the product of the appropriate factor loading and factor vectors plus the corresponding random error term (all highlighted in red).
is shown in red, and is computed from the product of the appropriate factor loading and factor vectors plus the corresponding random error term (all highlighted in red).
Figure 2. Illustration of two different ways that African and European individuals could be represented.
In the first (sparse) representation in the first row, the factors (shown in red) each represent the mean allele frequencies for either the African population ( ) or the European population (
) or the European population ( ); this lends to sparse loadings (shown in blue) for each individual, since the African individuals are only loaded on the factor representing the African population, and likewise for the European individuals. In the second (non-sparse) representation in the second row, each factor is a combination of
); this lends to sparse loadings (shown in blue) for each individual, since the African individuals are only loaded on the factor representing the African population, and likewise for the European individuals. In the second (non-sparse) representation in the second row, each factor is a combination of  and
and  , and each individual is loaded onto both factors. Note that the representations are equivalent by the equations under the table. Whereas SFA and admixture-based models tend to choose the first representation because of the sparse priors and implicit regularization, PCA tends towards the second representation (although the actual factors depend on other features of the data such as sample sizes of both groups).
, and each individual is loaded onto both factors. Note that the representations are equivalent by the equations under the table. Whereas SFA and admixture-based models tend to choose the first representation because of the sparse priors and implicit regularization, PCA tends towards the second representation (although the actual factors depend on other features of the data such as sample sizes of both groups).
Figure 3. Results of applying SFA, PCA, and admixture to the HapMap genotype data.
Each plot shows the estimated loadings ( -axis) across individuals (
-axis) across individuals ( -axis). SFA loadings are in the first row, PCA loadings in the second, and
-axis). SFA loadings are in the first row, PCA loadings in the second, and
admixture
loadings in the third. European individuals are denoted with blue ‘x’s, African individuals are denoted with red triangles, and Asian individuals are denoted with green ‘+’s. A dashed horizontal line is at zero on the  -axis.
-axis.
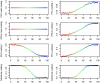
Figure 4. Estimated factor loadings from PCA, SFAm, SFA, and admixture for the 1-D isolation-by-distance simulation.
In each plot the individuals are colored and ordered along the  -axis by location in the 1-D habitat.
-axis by location in the 1-D habitat.
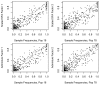
Figure 5. Estimated scaled factors from SFA and admixture on the 1-D isolation-by-distance simulation against the generating allele frequencies.
In each plot the factors ( -axis) are plotted against the population allele frequencies for the closest-matching population. The SFA factors were truncated to have a minimum of zero and scaled to have a maximum of one. The dashed diagonal line shows
-axis) are plotted against the population allele frequencies for the closest-matching population. The SFA factors were truncated to have a minimum of zero and scaled to have a maximum of one. The dashed diagonal line shows  .
.
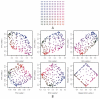
Figure 6. Results of SFA, PCA, SFAm, and admixture applied to simulated genotype data from a single 2-D habitat.
In Panel A, each dot represents a population colored according to location. In Panel B, each plot is of the loadings across individuals against each other, where the colors correspond to their locations in Panel A. The first row shows the three SFA loadings against each other from a three factor model. The second row shows the second two PCA loadings, the SFAm loadings, and the mapped
admixture
loadings (see text for details). All of the methods recapitulate, to a greater or lesser extent, the geographical structure of the habitats (up to rotation).
Figure 7. Results on simulated genotype data from a two independent 2-D habitats.
In Panel A, each dot represents a population colored according to habitat and location. Colors in Panels B and C indicate locations in Panel A. Panel B shows how SFA captures the structure with a six factor model. Loadings on the first three factors (first row of Panel B) correspond to location in the first habitat; individuals in the second habitat have essentially zero loading on these factors. Similarly, loadings on the other three factors (second row of Panel B) correspond to location in the second habitat. Panel C shows estimated loadings from PCA for the same data. Each plot shows one loading plotted against another. Although the PCA results clearly reflect the underlying structure one might struggle to infer the structure from visual inspection of these plots if the colors were unknown.
Figure 8. Results from SFA, admixture, and PCA for the clustered 1-D simulation.
All plots show the individuals on the  -axis (colored and ordered by location with respect to the 1-D clustered isolation-by-distance model) plotted against the estimated loadings.
-axis (colored and ordered by location with respect to the 1-D clustered isolation-by-distance model) plotted against the estimated loadings.
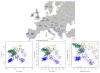
Figure 9. Results from PCA, SFAm, and admixture for the POPRES European data.
These results were rotated (but not rescaled) to make the correspondence to the map of Europe more immediately obvious. The results from SFAm are very similar to the results from PCA for these data, effectively recapitulating the geography of Europe.
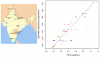
Figure 10. Plot of estimated admixture proportions of each Indian group versus the relative admixture proportions from SFA on the Indian data set.
This plot shows good correlation between the relative admixture proportions from SFA and the estimated admixture proportions from previous work. The colors coding the groups are described in the India map.
Similar articles
- Inferring Population Structure and Admixture Proportions in Low-Depth NGS Data.
Meisner J, Albrechtsen A. Meisner J, et al. Genetics. 2018 Oct;210(2):719-731. doi: 10.1534/genetics.118.301336. Epub 2018 Aug 21. Genetics. 2018. PMID: 30131346 Free PMC article. - A novel and fast approach for population structure inference using kernel-PCA and optimization.
Popescu AA, Harper AL, Trick M, Bancroft I, Huber KT. Popescu AA, et al. Genetics. 2014 Dec;198(4):1421-31. doi: 10.1534/genetics.114.171314. Epub 2014 Oct 16. Genetics. 2014. PMID: 25326237 Free PMC article. - A Likelihood-Free Estimator of Population Structure Bridging Admixture Models and Principal Components Analysis.
Cabreros I, Storey JD. Cabreros I, et al. Genetics. 2019 Aug;212(4):1009-1029. doi: 10.1534/genetics.119.302159. Epub 2019 Apr 26. Genetics. 2019. PMID: 31028112 Free PMC article. - [The application of statistical approaches in studying population genetics with STR data].
Gui HS, Yang L, Li SB. Gui HS, et al. Yi Chuan. 2007 Dec;29(12):1443-8. Yi Chuan. 2007. PMID: 18065377 Review. Chinese. - Population identification using genetic data.
Lawson DJ, Falush D. Lawson DJ, et al. Annu Rev Genomics Hum Genet. 2012;13:337-61. doi: 10.1146/annurev-genom-082410-101510. Epub 2012 Jun 11. Annu Rev Genomics Hum Genet. 2012. PMID: 22703172 Review.
Cited by
- Empirical Bayes Matrix Factorization.
Wang W, Stephens M. Wang W, et al. J Mach Learn Res. 2021;22:120. J Mach Learn Res. 2021. PMID: 37920532 Free PMC article. - Genetic Ancestry Estimates within Dutch Family Units and Across Genotyping Arrays: Insights from Empirical Analysis Using Two Estimation Methods.
Beck JJ, Ahmed T, Finnicum CT, Zwinderman K, Ehli EA, Boomsma DI, Hottenga JJ. Beck JJ, et al. Genes (Basel). 2023 Jul 22;14(7):1497. doi: 10.3390/genes14071497. Genes (Basel). 2023. PMID: 37510400 Free PMC article. - A Fast, Provably Accurate Approximation Algorithm for Sparse Principal Component Analysis Reveals Human Genetic Variation Across the World.
Chowdhury A, Bose A, Zhou S, Woodruff DP, Drineas P. Chowdhury A, et al. Res Comput Mol Biol. 2022 May;13278:86-106. doi: 10.1007/978-3-031-04749-7_6. Epub 2022 Apr 29. Res Comput Mol Biol. 2022. PMID: 36649383 Free PMC article. - Non-negative Independent Factor Analysis disentangles discrete and continuous sources of variation in scRNA-seq data.
Mao W, Pouyan MB, Kostka D, Chikina M. Mao W, et al. Bioinformatics. 2022 May 13;38(10):2749-2756. doi: 10.1093/bioinformatics/btac136. Bioinformatics. 2022. PMID: 35561207 Free PMC article. - A geometric relationship of _F_2, _F_3 and _F_4-statistics with principal component analysis.
Peter BM. Peter BM. Philos Trans R Soc Lond B Biol Sci. 2022 Jun 6;377(1852):20200413. doi: 10.1098/rstb.2020.0413. Epub 2022 Apr 18. Philos Trans R Soc Lond B Biol Sci. 2022. PMID: 35430884 Free PMC article.
References
- Rosenberg NA, Pritchard JK, Weber JL, Cann HM, Kidd KK, et al. Genetic Structure of Human Populations. Science. 2002;298:2381–2385. - PubMed
- Parker HG, Kim LV, Sutter NB, Carlson S, Lorentzen TD, et al. Genetic Structure of the Purebred Domestic Dog. Science. 2004;304:1160–1164. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources