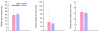Accumulation of driver and passenger mutations during tumor progression - PubMed (original) (raw)

Accumulation of driver and passenger mutations during tumor progression

Ivana Bozic et al. Proc Natl Acad Sci U S A. 2010.

Abstract

Major efforts to sequence cancer genomes are now occurring throughout the world. Though the emerging data from these studies are illuminating, their reconciliation with epidemiologic and clinical observations poses a major challenge. In the current study, we provide a mathematical model that begins to address this challenge. We model tumors as a discrete time branching process that starts with a single driver mutation and proceeds as each new driver mutation leads to a slightly increased rate of clonal expansion. Using the model, we observe tremendous variation in the rate of tumor development-providing an understanding of the heterogeneity in tumor sizes and development times that have been observed by epidemiologists and clinicians. Furthermore, the model provides a simple formula for the number of driver mutations as a function of the total number of mutations in the tumor. Finally, when applied to recent experimental data, the model allows us to calculate the actual selective advantage provided by typical somatic mutations in human tumors in situ. This selective advantage is surprisingly small--0.004 ± 0.0004--and has major implications for experimental cancer research.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Fig. 1.

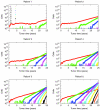
Fig. 1.

Variability in tumor progression. Number of cells with a given number of driver mutations versus the age of the tumor. Six different realizations of the same stochastic process with the same parameter values are shown, corresponding to tumor growth in six patients. The process is initiated with a single surviving founder cell with one driver mutation. The times at which subsequent driver mutations arose varied widely among patients. After initial stochastic fluctuations, each new mutant lineage grew exponentially. The overall dynamics of tumor growth are greatly affected by the random time of the appearance of new mutants with surviving lineages. Parameter values: mutation rate u = 3.4 × 10-5, selective advantage s = 0.4%, and generation time T = 3 d.

Fig. 2.

Fig. 2.

Schematic representation of waves of clonal expansions. An illustration of a sequence of clonal expansions of cells with k = 1, 2, 3, or 4 driver mutations is shown. Here _τ_1 is the average time it takes the lineage of the founder cell to produce a successful cell with two driver mutations. Similarly, τ k is the average time between the appearance of cells with k and k + 1 mutations. Eq. 1 gives a simple formula for these waiting times, which shows that subsequent driver mutations appear faster and faster. The cumulative time to have k driver mutations grows with the logarithm of k.

Fig. 3.

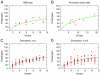
Fig. 3.

Comparison of clinical mutation data and theory. Our theory provides an estimate for the number of passenger mutations in a tumor as a function of the number of driver mutations. Parameter values used in Eq. 2 and computer simulations were s = 0.4% and u = 3.4 × 10-5. (A) Eq. 2 (green line) fitted to GBM data. (B) Eq. 2 (green line) fitted to pancreatic cancer data. (C) Comparison of computer simulations and Eq. 2. For each k between 2 and 10, the number of passengers that were brought along with the last driver in 10 tumors with k drivers is plotted. Blue circles represent averages from 100 simulations. (D) Comparison between computer simulations and Eq. 2 for selective advantage of the _k_th driver, s k, taken from a Gaussian distribution with mean s and standard deviation σ = s/2. For each k between 2 and 10, the number of passengers that were brought along with the last driver in 10 tumors with k drivers is plotted. Blue circles represent averages from 100 simulations. Note that in A, the tumor with only one driver mutation has 16 passenger mutations, instead of the theoretically predicted zero. A possible reason for this discrepancy could be that the CHASM algorithm did not manage to classify all driver mutations as such, or perhaps that the ancestry of the founder cell of the tumor experienced a significant level of proliferation before the onset of neoplasia.

Fig. 4.

Fig. 4.

Comparison of clinical FAP data and computer simulations of our model. A uniform random age < 40 was picked first and only those patients who had at least five polyps and no history of cancer at the sampled age were retained. We compared the number and size of the polyps in these patients with the clinical data on number and size of polyps in FAP patients at study (37) entry. The age distribution of patients from the simulation was compared to the age distribution of patients in the study (37). Parameter values used in simulations are s = 0.4%, u = 3.4 × 10-5, T = 4 days, and polyp initiation rate 32 per week. Error bars represent standard deviation.

Comment in

Similar articles

Cited by

References

    1. Vogelstein B, Kinzler KW. Cancer genes and the pathways they control. Nat Med. 2004;10:789–799. - PubMed
    1. Greenman C, et al. Patterns of somatic mutation in human cancer genomes. Nature. 2007;446:153–158. - PMC - PubMed
    1. Collins FS, Barker AD. Mapping the cancer genome. Sci Am. 2007;296:50–57. - PubMed
    1. Ley TJ, et al. DNA sequencing of a cytogenetically normal acute myeloid leukemia genome. Nature. 2008;456:66–72. - PMC - PubMed
    1. Mardis ER, et al. Recurring mutations found by sequencing an acute myeloid leukemia genome. N Engl J Med. 2009;361:1058–66. - PMC - PubMed

Publication types

MeSH terms

Grants and funding

LinkOut - more resources