An introduction to maximum-likelihood methods in cryo-EM - PubMed (original) (raw)
An introduction to maximum-likelihood methods in cryo-EM
Fred J Sigworth et al. Methods Enzymol. 2010.
Abstract
The maximum-likelihood method provides a powerful approach to many problems in cryo-electron microscopy (cryo-EM) image processing. This contribution aims to provide an accessible introduction to the underlying theory and reviews existing applications in the field. In addition, current developments to reduce computational costs and to improve the statistical description of cryo-EM images are discussed. Combined with the increasing power of modern computers and yet unexplored possibilities provided by theory, these developments are expected to turn the statistical approach into an essential image-processing tool for the electron microscopist.
Copyright © 2010 Elsevier Inc. All rights reserved.
Figures
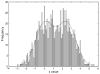
Figure 1
Histogram of values of a random variable x. The values were drawn from a distribution consisting of a mixture of two Gaussians with means of 0 and 2.5.
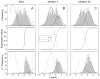
Figure 2
EM-ML estimation of the means and amplitudes in a mixture of two Gaussians as in Figure 1. A, top panel, a histogram of 1000 simulated measurements is shown, along with two Gaussian components computed on the basis of initial guesses for the mean and amplitude of the components. The middle panel shows how the expectation ŷ varies with the measured value x. Instead of there being a strict classification of x values into one or the other component, these ŷ values take on intermediate values in the range of x values where the components overlap. The bottom panel illustrates how a weighted average can give rise to the mean value for the left-hand component. The bins of the histogram have been scaled by the values of ŷ, while the initial guess of the PDF is plotted as a smooth curve. The center of mass of the weighted histogram yields the new estimate for _μ_1. B, the same plots are shown after the two Gaussian components have been updated with new means and amplitudes by one EM-ML iteration. C, the result after convergence with 24 iterations. The simulation was based on means of 0 and 2.5. The EM-ML estimated means were −0.06 and 2.46.
Figure 3
An example of direct MLE calculation. A, an image A with a zoom window centered on one individual pixel value with value Aj is shown. B, three copies of image A with different instances of white Gaussian noise are shown together with zoom windows on the same pixel j with pixel values X_1_j, X_2_j and X_3_j. C, the PDF of the _j_th pixel in the noisy images is shown as a Gaussian curve centered at Aj and with standard deviation σ. Direct calculation of AjMLE is performed by averaging over X_1_j, X_2_j and X_3_j. D, the MLE of the entire image A is shown together with a zoom window, centered on AjMLE. Note that the MLE of the image will approach the image in A if larger numbers of noisy images are available.
Figure 4
The PDF of a noisy image as a function of its relative orientation with respect to a reference image. A, Xi, a rotated and noisy version of reference image A from Figure 3A is shown. B, top panel, the probability P(Xi|φ, Θ) of observing Xi given a model Θ that comprises image A is shown (on an arbitrary scale) as a function of the relative orientation φ. The bottom panel shows RφA, i.e. image A rotated according to φ. Note that P (Xi|φ, Θ) is highest when φ corresponds to the correct orientation of Xi.
Figure 5
Reference image calculation by probability-weighted averaging. A, three noisy versions of reference image A from Figure 3A in different orientations (Xi, with i = 1, 2, 3). B, images Rφ−1Xi for all sampled φ. The opacity of the images is used to illustrate the weight P(φ|Xi, Θ(n)) in the weighted average calculation that produces the updated estimate of the reference A(n+1), see Eq. (24). Note that _X_1 corresponds to the same image that was shown in Figure 4A and that the columns correspond to the same orientations as in Figure 4B.
Similar articles
- SubspaceEM: A fast maximum-a-posteriori algorithm for cryo-EM single particle reconstruction.
Dvornek NC, Sigworth FJ, Tagare HD. Dvornek NC, et al. J Struct Biol. 2015 May;190(2):200-14. doi: 10.1016/j.jsb.2015.03.009. Epub 2015 Mar 31. J Struct Biol. 2015. PMID: 25839831 Free PMC article. - Robustness of signal detection in cryo-electron microscopy via a bi-objective-function approach.
Wang WL, Yu Z, Castillo-Menendez LR, Sodroski J, Mao Y. Wang WL, et al. BMC Bioinformatics. 2019 Apr 3;20(1):169. doi: 10.1186/s12859-019-2714-8. BMC Bioinformatics. 2019. PMID: 30943890 Free PMC article. - Electron cryo-microscopy for elucidating the dynamic nature of live-protein complexes.
Shigematsu H. Shigematsu H. Biochim Biophys Acta Gen Subj. 2020 Feb;1864(2):129436. doi: 10.1016/j.bbagen.2019.129436. Epub 2019 Sep 13. Biochim Biophys Acta Gen Subj. 2020. PMID: 31525409 Review. - Focus: The interface between data collection and data processing in cryo-EM.
Biyani N, Righetto RD, McLeod R, Caujolle-Bert D, Castano-Diez D, Goldie KN, Stahlberg H. Biyani N, et al. J Struct Biol. 2017 May;198(2):124-133. doi: 10.1016/j.jsb.2017.03.007. Epub 2017 Mar 23. J Struct Biol. 2017. PMID: 28344036 - Cryo electron microscopy to determine the structure of macromolecular complexes.
Carroni M, Saibil HR. Carroni M, et al. Methods. 2016 Feb 15;95:78-85. doi: 10.1016/j.ymeth.2015.11.023. Epub 2015 Nov 27. Methods. 2016. PMID: 26638773 Free PMC article. Review.
Cited by
- Locating macromolecular assemblies in cells by 2D template matching with cisTEM.
Lucas BA, Himes BA, Xue L, Grant T, Mahamid J, Grigorieff N. Lucas BA, et al. Elife. 2021 Jun 11;10:e68946. doi: 10.7554/eLife.68946. Elife. 2021. PMID: 34114559 Free PMC article. - An approach to improve the resolution of helical filaments with a large axial rise and flexible subunits.
Yang S, Woodhead JL, Zhao FQ, Sulbarán G, Craig R. Yang S, et al. J Struct Biol. 2016 Jan;193(1):45-54. doi: 10.1016/j.jsb.2015.11.007. Epub 2015 Nov 22. J Struct Biol. 2016. PMID: 26592473 Free PMC article. - Fast multiscale reconstruction for Cryo-EM.
Donati L, Nilchian M, Sorzano COS, Unser M. Donati L, et al. J Struct Biol. 2018 Dec;204(3):543-554. doi: 10.1016/j.jsb.2018.09.008. Epub 2018 Sep 24. J Struct Biol. 2018. PMID: 30261282 Free PMC article. - Covariance Matrix Estimation for the Cryo-EM Heterogeneity Problem.
Katsevich E, Katsevich A, Singer A. Katsevich E, et al. SIAM J Imaging Sci. 2015 Jan 22;8(1):126-185. doi: 10.1137/130935434. SIAM J Imaging Sci. 2015. PMID: 25699132 Free PMC article. - Hyper-Molecules: on the Representation and Recovery of Dynamical Structures for Applications in Flexible Macro-Molecules in Cryo-EM.
Lederman RR, Andén J, Singer A. Lederman RR, et al. Inverse Probl. 2020 Apr;36(4):044005. doi: 10.1088/1361-6420/ab5ede. Epub 2020 Mar 4. Inverse Probl. 2020. PMID: 38304203 Free PMC article.
References
- Al-Amoudi A, Diez DC, Betts MJ, Frangakis AS. The molecular architecture of cadherins in native epidermal desmosomes. Nature. 2007;450:832–837. - PubMed
- Chen Q. Master’s thesis. School of Electrical and Computer Engineering, Cornell University; 2008. Nonlinear stochastic tomography reconstruction algorithms for objects with helical symmetry and applications to virus structures.
- Cheng Y, Walz T. The advent of Near-Atomic resolution in Single-Particle electron microscopy. Annu Rev Biochem. 2009;78:723–742. - PubMed
- Dempster AP, Laird NM, Rubin DB. Maximum-likelihood from incomplete data via the EM algorithm. J Royal Statist Soc Ser B. 1977;39:1–38.
Publication types
MeSH terms
Grants and funding
- P01-GM062580/GM/NIGMS NIH HHS/United States
- R01 HL070472/HL/NHLBI NIH HHS/United States
- R01 HL070472-08/HL/NHLBI NIH HHS/United States
- MC_UP_A025_1013/MRC_/Medical Research Council/United Kingdom
- R01HL070472/HL/NHLBI NIH HHS/United States
- P01 GM062580/GM/NIGMS NIH HHS/United States
LinkOut - more resources
Full Text Sources