An accurate sequentially Markov conditional sampling distribution for the coalescent with recombination - PubMed (original) (raw)

An accurate sequentially Markov conditional sampling distribution for the coalescent with recombination

Joshua S Paul et al. Genetics. 2011 Apr.

Abstract

The sequentially Markov coalescent is a simplified genealogical process that aims to capture the essential features of the full coalescent model with recombination, while being scalable in the number of loci. In this article, the sequentially Markov framework is applied to the conditional sampling distribution (CSD), which is at the core of many statistical tools for population genetic analyses. Briefly, the CSD describes the probability that an additionally sampled DNA sequence is of a certain type, given that a collection of sequences has already been observed. A hidden Markov model (HMM) formulation of the sequentially Markov CSD is developed here, yielding an algorithm with time complexity linear in both the number of loci and the number of haplotypes. This work provides a highly accurate, practical approximation to a recently introduced CSD derived from the diffusion process associated with the coalescent with recombination. It is empirically demonstrated that the improvement in accuracy of the new CSD over previously proposed HMM-based CSDs increases substantially with the number of loci. The framework presented here can be adopted in a wide range of applications in population genetics, including imputing missing sequence data, estimating recombination rates, and inferring human colonization history.

PubMed Disclaimer

Figures

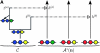
F<sc>igure</sc> 1.—

Figure 1.—

Illustration of the corresponding genealogical and sequential interpretations for a realization of formula image. The three loci of each haplotype are each represented by a solid circle, with the color indicating the allelic type at that locus. The trunk genealogy 𝒜*(n) and conditional genealogy C are indicated. Time is represented vertically, with the present (time 0) at the bottom of the illustration. (A) The genealogical interpretation: Mutation events, along with the locus and resulting haplotype, are indicated by small arrows. Recombination events, and the resulting haplotype, are indicated by branching events in C. Absorption events, and the corresponding absorption time [t(a) and t(b)] and haplotype [h(a) and h(b), respectively], are indicated by dotted-dashed horizontal lines. (B) The corresponding sequential interpretation: The marginal genealogies at the first, second, and third locus (_S_1, _S_2, and _S_3) are emphasized as dotted, dashed, and solid lines, respectively. Mutation events at each locus, along with resulting allele, are indicated by small arrows. Absorption events at each locus are indicated by horizontal lines.

F<sc>igure</sc> 1.—

Figure 1.—

Illustration of the corresponding genealogical and sequential interpretations for a realization of formula image. The three loci of each haplotype are each represented by a solid circle, with the color indicating the allelic type at that locus. The trunk genealogy 𝒜*(n) and conditional genealogy C are indicated. Time is represented vertically, with the present (time 0) at the bottom of the illustration. (A) The genealogical interpretation: Mutation events, along with the locus and resulting haplotype, are indicated by small arrows. Recombination events, and the resulting haplotype, are indicated by branching events in C. Absorption events, and the corresponding absorption time [t(a) and t(b)] and haplotype [h(a) and h(b), respectively], are indicated by dotted-dashed horizontal lines. (B) The corresponding sequential interpretation: The marginal genealogies at the first, second, and third locus (_S_1, _S_2, and _S_3) are emphasized as dotted, dashed, and solid lines, respectively. Mutation events at each locus, along with resulting allele, are indicated by small arrows. Absorption events at each locus are indicated by horizontal lines.

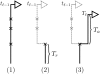
F<sc>igure</sc> 2.—

Figure 2.—

Illustration of the (Markov) process for sampling the absorption time _T_ℓ given the absorption time _T_ℓ−1 = t_ℓ−1. In step 1, recombination breakpoints are realized as a Poisson process with rate ρ_b/2 on the marginal conditional genealogy with absorption time _t_ℓ−1. In step 2, the lineage branching from each breakpoint associated with locus ℓ−1 is removed, so that only the lineage more recent than the first breakpoint, at time _T_r, remains. In step 3, the lineage branching from the first recombination breakpoint associated with locus ℓ is absorbed after time _T_a distributed exponentially with rate n/2. Thus, _T_ℓ = _T_r + _T_a.

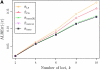
F<sc>igure</sc> 3.—

Figure 3.—

Absolute log-ratio error (ALRErr) of various conditional sampling distributions. See (22) for a formal definition of ALRErr_k,n_(· | ·). The accuracy of formula image is almost indistinguishable from that of formula image, the most accurate of all approximate CSDs considered here. As expected, discretization reduces the accuracy somewhat, but even formula image is substantially more accurate than formula image and formula image. With θ0 = 0.01 and ρ0 = 0.05, we used the methodology described in the text to sample 250 conditional configurations, each with n = 10 haplotypes and k loci. (A) Error is measured relative to the true CSD π, estimated using computationally intensive importance sampling. (B) Error is measured relative to formula image, computed by numerically solving a recursion for the equivalent CSD formula image.

F<sc>igure</sc> 3.—

Figure 3.—

Absolute log-ratio error (ALRErr) of various conditional sampling distributions. See (22) for a formal definition of ALRErr_k,n_(· | ·). The accuracy of formula image is almost indistinguishable from that of formula image, the most accurate of all approximate CSDs considered here. As expected, discretization reduces the accuracy somewhat, but even formula image is substantially more accurate than formula image and formula image. With θ0 = 0.01 and ρ0 = 0.05, we used the methodology described in the text to sample 250 conditional configurations, each with n = 10 haplotypes and k loci. (A) Error is measured relative to the true CSD π, estimated using computationally intensive importance sampling. (B) Error is measured relative to formula image, computed by numerically solving a recursion for the equivalent CSD formula image.

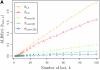
F<sc>igure</sc> 4.—

Figure 4.—

Comparison of the accuracy of various conditional sampling distributions relative to formula image (see Figure 3 for the accuracy of formula image). A and B illustrate that the improvement in accuracy of formula image over formula image and formula image is amplified as the number of loci k increases and that both formula image and formula image produce significantly smaller values than formula image (and formula image). For θ0 = 0.01 and ρ0 = 0.05, we used the methodology described in the text to sample 250 conditional configurations with n = 10 haplotypes and k loci. (A) Absolute log-ratio error. (B) Signed log-ratio error.

F<sc>igure</sc> 4.—

Figure 4.—

Comparison of the accuracy of various conditional sampling distributions relative to formula image (see Figure 3 for the accuracy of formula image). A and B illustrate that the improvement in accuracy of formula image over formula image and formula image is amplified as the number of loci k increases and that both formula image and formula image produce significantly smaller values than formula image (and formula image). For θ0 = 0.01 and ρ0 = 0.05, we used the methodology described in the text to sample 250 conditional configurations with n = 10 haplotypes and k loci. (A) Absolute log-ratio error. (B) Signed log-ratio error.

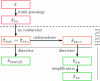
F<sc>igure</sc> 5.—

Figure 5.—

Illustration of the relationship between various CSDs. The CSD at the head of each arrow can be seen as an approximation to the CSD at the tail. Each arrow is also annotated with a (short) description of this approximation. The CSDs below the dashed line can be cast as an HMM: Those above the dotted line (including a continuous-state version of formula image, which we denote formula image) have a continuous and infinite state space, while those below have a finite and discrete state space and are therefore amenable to simple dynamic programming algorithms. For more thorough descriptions of each approximation, see the main text and also P

aul

and S

ong

(2010). Recall in particular that the equality formula image holds only for conditionally sampling a single haplotype.

Similar articles

Cited by

References

    1. Abramowitz, M., and I. A. Stegun (Editors), 1972. Handbook of Mathematical Functions With Formulas, Graphs, and Mathematical Tables. Dover, New York.
    1. Chen, G. K., P. Marjoram and J. D. Wall, 2009. Fast and flexible simulation of DNA sequence data. Genome Res. 19 136–142. - PMC - PubMed
    1. Crawford, D. C., T. Bhangale, N. Li, G. Hellenthal, M. J. Rieder et al., 2004. Evidence for substantial fine-scale variation in recombination rates across the human genome. Nat. Genet. 36 700–706. - PubMed
    1. Davison, D., J. K. Pritchard and G. Coop, 2009. An approximate likelihood for genetic data under a model with recombination and population splitting. Theor. Popul. Biol. 75(4): 331–345. - PMC - PubMed
    1. De Iorio, M., and R. C. Griffiths, 2004. a Importance sampling on coalescent histories. I. Adv. Appl. Probab. 36(2): 417–433.

Publication types

MeSH terms

Grants and funding

LinkOut - more resources