The fractal globule as a model of chromatin architecture in the cell - PubMed (original) (raw)
The fractal globule as a model of chromatin architecture in the cell
Leonid A Mirny. Chromosome Res. 2011 Jan.
Abstract
The fractal globule is a compact polymer state that emerges during polymer condensation as a result of topological constraints which prevent one region of the chain from passing across another one. This long-lived intermediate state was introduced in 1988 (Grosberg et al. 1988) and has not been observed in experiments or simulations until recently (Lieberman-Aiden et al. 2009). Recent characterization of human chromatin using a novel chromosome conformational capture technique brought the fractal globule into the spotlight as a structural model of human chromosome on the scale of up to 10 Mb (Lieberman-Aiden et al. 2009). Here, we present the concept of the fractal globule, comparing it to other states of a polymer and focusing on its properties relevant for the biophysics of chromatin. We then discuss properties of the fractal globule that make it an attractive model for chromatin organization inside a cell. Next, we connect the fractal globule to recent studies that emphasize topological constraints as a primary factor driving formation of chromosomal territories. We discuss how theoretical predictions, made on the basis of the fractal globule model, can be tested experimentally. Finally, we discuss whether fractal globule architecture can be relevant for chromatin packing in other organisms such as yeast and bacteria.
Figures
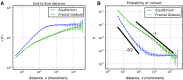
Fig. 1
a Root-mean squared end-to-end distance R(s) as a function of the genomic distance s between the ends of a subchain (in the units of ) for globules of N = 32,000 monomers. Blue, equilibrium globule; green, fractal globule. At small s, both globules show scaling characteristic of the self-avoiding random walk (3/5), followed by 1/2 of the ideal coil. Notice there is a plateau for the equilibrium globule. b The probability of a contact as a function of genomic distance s for the equilibrium globule (blue) and the fractal globule (green). Notice the robust scaling of −1 which spans two orders of magnitude for the fractal globule
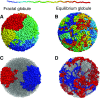
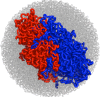
Fig. 2
Conformations of the fractal (a) and equilibrium (b) globules. The chain is colored from red to blue in rainbow colors as shown on the top. The fractal globule has a striking territorial organization, which strongly contrasts with the mixing observed in the equilibrium globule. Territorial organization of the fractal globule (c) is evident when two chains of 1,000 monomers each are outlined. The equilibrium globule (d), in contrast, has two chains mixed together in space
Fig. 3
The fractal globule (a) consist of dense globules formed on all scales. Subchains of 100, 300, 1,000, and 3,000 monomers (left to right) are shown by a red tube in a globule of N = 32,000 monomers. For comparison, same regions of the equilibrium globule (b) are diffuse inside the globule
Fig. 4
Opening of a loop that is a part of the fractal globule (a), and the equilibrium globule (b). Globules of 32,000 monomers were folded by pairwise attractive interactions. The fractal globule was formed by Molecular Dynamics which keeps track of topological constrains, while the equilibrium globule was equilibrated folded by Monte Carlo simulations (Reith and Virnau 2010) that violate topological constrains leading to significant entanglement. On the next step of molecular dynamics simulation, attractive interactions for a region of 3,000 monomers were removed allowing the region to open up due to the chain entropy. In the fractal globule, the region opened up forming a large loop (a). The same region failed to open from the equilibrium globule (b) due chain entanglements in this state
Fig. 5
Despite having an organized territorial architecture, spatially neighboring regions of the fractal globule (shown in red and blue) have a large number of interactions between them, deeply penetrating into each other's volumes. The number of interactions of crumples has scales linear with its volumes (see Eq. 12). Thus a fixed fraction of crumples volume (rather than its surface) is involved in interactions.
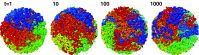
Fig. 6
Equilibration of the fractal globule. A series of snapshots obtained at four logarithmically spaced timepoints of long equilibration simulations. Notice gradual loss of the territorial organization, characteristic of the fractal globule, and increasing mixing, leading to formation of the equilibrium globule. Since the ends of the globule remain attached to the surface while being able to slide on it, the structure remains unentangled. This equilibration is very slow. The details of these simulations will be published elsewhere
Similar articles
- On the stability of fractal globules.
Schram RD, Barkema GT, Schiessel H. Schram RD, et al. J Chem Phys. 2013 Jun 14;138(22):224901. doi: 10.1063/1.4807723. J Chem Phys. 2013. PMID: 23781815 - Anomalous diffusion in fractal globules.
Tamm MV, Nazarov LI, Gavrilov AA, Chertovich AV. Tamm MV, et al. Phys Rev Lett. 2015 May 1;114(17):178102. doi: 10.1103/PhysRevLett.114.178102. Epub 2015 Apr 30. Phys Rev Lett. 2015. PMID: 25978267 - A fractal model for nuclear organization: current evidence and biological implications.
Bancaud A, Lavelle C, Huet S, Ellenberg J. Bancaud A, et al. Nucleic Acids Res. 2012 Oct;40(18):8783-92. doi: 10.1093/nar/gks586. Epub 2012 Jul 11. Nucleic Acids Res. 2012. PMID: 22790985 Free PMC article. Review. - History-dependent nonequilibrium conformations of a highly confined polymer globule in a sphere.
Kwon S, Sung BJ. Kwon S, et al. Phys Rev E. 2020 Aug;102(2-1):022501. doi: 10.1103/PhysRevE.102.022501. Phys Rev E. 2020. PMID: 32942375 - Relevance and limitations of crowding, fractal, and polymer models to describe nuclear architecture.
Huet S, Lavelle C, Ranchon H, Carrivain P, Victor JM, Bancaud A. Huet S, et al. Int Rev Cell Mol Biol. 2014;307:443-79. doi: 10.1016/B978-0-12-800046-5.00013-8. Int Rev Cell Mol Biol. 2014. PMID: 24380602 Review.
Cited by
- Stress-induced RNA-chromatin interactions promote endothelial dysfunction.
Calandrelli R, Xu L, Luo Y, Wu W, Fan X, Nguyen T, Chen CJ, Sriram K, Tang X, Burns AB, Natarajan R, Chen ZB, Zhong S. Calandrelli R, et al. Nat Commun. 2020 Oct 15;11(1):5211. doi: 10.1038/s41467-020-18957-w. Nat Commun. 2020. PMID: 33060583 Free PMC article. - Understanding spatial organizations of chromosomes via statistical analysis of Hi-C data.
Hu M, Deng K, Qin Z, Liu JS. Hu M, et al. Quant Biol. 2013 Jun;1(2):156-174. doi: 10.1007/s40484-013-0016-0. Quant Biol. 2013. PMID: 26124977 Free PMC article. - Colocalization of coregulated genes: a steered molecular dynamics study of human chromosome 19.
Di Stefano M, Rosa A, Belcastro V, di Bernardo D, Micheletti C. Di Stefano M, et al. PLoS Comput Biol. 2013;9(3):e1003019. doi: 10.1371/journal.pcbi.1003019. Epub 2013 Mar 28. PLoS Comput Biol. 2013. PMID: 23555238 Free PMC article. - The radial nuclear positioning of genes correlates with features of megabase-sized chromatin domains.
Kölbl AC, Weigl D, Mulaw M, Thormeyer T, Bohlander SK, Cremer T, Dietzel S. Kölbl AC, et al. Chromosome Res. 2012 Aug;20(6):735-52. doi: 10.1007/s10577-012-9309-9. Epub 2012 Sep 28. Chromosome Res. 2012. PMID: 23053570 - Mesoscale Modeling Reveals Hierarchical Looping of Chromatin Fibers Near Gene Regulatory Elements.
Bascom GD, Sanbonmatsu KY, Schlick T. Bascom GD, et al. J Phys Chem B. 2016 Aug 25;120(33):8642-53. doi: 10.1021/acs.jpcb.6b03197. Epub 2016 Jun 16. J Phys Chem B. 2016. PMID: 27218881 Free PMC article.
References
- Alberts B. Molecular biology of the cell. New York: Garland Science; 2008.
- Alberts B. Molecular biology of the cell: chapter 7. New York: Garland Science; 2008.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Molecular Biology Databases
Miscellaneous