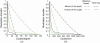Optical properties of the mouse eye - PubMed (original) (raw)
Optical properties of the mouse eye
Ying Geng et al. Biomed Opt Express. 2011.
Abstract
The Shack-Hartmann wavefront sensor (SHWS) spots upon which ocular aberration measurements depend have poor quality in mice due to light reflected from multiple retinal layers. We have designed and implemented a SHWS that can favor light from a specific retinal layer and measured monochromatic aberrations in 20 eyes from 10 anesthetized C57BL/6J mice. Using this instrument, we show that mice are myopic, not hyperopic as is frequently reported. We have also measured longitudinal chromatic aberration (LCA) of the mouse eye and found that it follows predictions of the water-filled schematic mouse eye. Results indicate that the optical quality of the mouse eye assessed by measurement of its aberrations is remarkably good, better for retinal imaging than the human eye. The dilated mouse eye has a much larger numerical aperture (NA) than that of the dilated human eye (0.5 NA vs. 0.2 NA), but it has a similar amount of root mean square (RMS) higher order aberrations compared to the dilated human eye. These measurements predict that adaptive optics based on this method of wavefront sensing will provide improvements in retinal image quality and potentially two times higher lateral resolution than that in the human eye.
Keywords: (110.1080) Active or adaptive optics; (170.4460) Medical optics and biotechnology: Ophthalmic optics and devices; (330.4300) Vision system - noninvasive assessment; (330.5370) Vision, color, and visual optics: Physiological optics; (330.7324) Vision, color, and visual optics: Visual optics, comparative animal models.
Figures
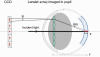
Fig. 1
Schematic explaining the elongation of wavefront sensor spots in the mouse eye. θ: elongation angle. n: refractive index of the retina. Note that the lenslets are in a plane conjugate to the eye’s pupil, and not physically on it.
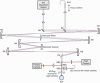
Fig. 2
Schematic of the mouse eye wavefront sensor. SLD: fiber coupled Super Luminescent Diode. SH Wavefront Sensor: Shack-Hartmann wavefront sensor. BS: Beam Splitter. RBS: Removable Beam Splitter. FM: Fold Mirror. M1-6: Concave spherical Mirrors.
Fig. 3
(a) Typical non-optimized wavefront sensor spot pattern in the mouse eye with a cross section of a single spot shown below. (b) An OCT line scan image with a cross section on a particular retinal location. OCT signal vs. depth for the cross section is shown below in linear scale. Both the wavefront spots and the OCT image show back reflections from two major layers from the retina. (c) Improved wavefront spots when the beacon is focused on the outer retina, when source focus was set at ~-10 D. Cross section of a single spot is shown below. Solid line: normalized intensity profile for the cross section. Dashed line: diffraction-limited spot profile for a lenslet. (d) An even sharper spot pattern can be obtained when the beacon is focused on the disk, when the source focus was set at ~20 D. Cross section of a single spot is shown below. Solid line: normalized intensity profile for the cross section. Dashed line: diffraction-limited spot profile for a lenslet. The wavefront sensor spots are very close to diffraction-limited. (e) An OCT line scan image taken on the optic disk with a cross section on the central retinal artery. OCT signal vs. depth for the cross secion is shown below in linear scale.
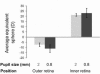
Fig. 4
Average equivalent sphere of mice eyes measured in two different positions over two pupil sizes. Left column: spherical equivalent measured on the outer retina. Right column: spherical equivalent measured on the inner retina. Light gray bars: spherical equivalent for 2 mm pupil size. Dark gray bars: spherical equivalent for 0.8 mm pupil size. Error bar: ± 2 times SEM.
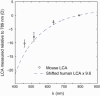
Fig. 5
Experimental data for mouse eye longitudinal chromatic aberration (LCA) and comparisons to theoretical estimates of the mouse eye LCA using human experimental data. Blue dashed lines: estimates of the mouse eye LCA using human LCA data and the water-filled reduced schematic eye. Circle data points: average LCA between wavelengths of 457, 514 and 633 nm, and reference wavelength 789 nm. For example, an average of 10.3 D of chromatic aberration is measured between 457 nm and 789 nm. Error bar: ± 2 SEM.
Fig. 6
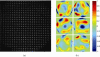
(a) Typical wavefront sensor spot pattern in the mouse eye used for measurement. Image is captured at 2.2 mm pupil size and wavefront is analyzed at 2 mm pupil size. (b) Higher order aberration wavefront maps for 6 eyes from 3 mice for 2 mm pupil size.
Fig. 7
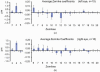
Mean values of 2nd to 5th order Zernike modes for 20 eyes across a 2 mm pupil, using wavefront spots focused on the outer retina. Zernikes for the 10 left eyes are shown in (a) and ones for the 10 right eyes are shown in (b). Error bars represent ± 2 times SEM. Lower and higher order aberrations are shown using different scales.
Fig. 8
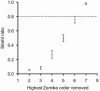
Strehl ratio for the 20 eyes over a 2 mm pupil at a wavelength of 789 nm. Error bars represent ± 2 SEM. Each data point shows the calculated Strehl ratio after a number of lower order aberrations are corrected. For example, the number 5 means that second, third, fourth and fifth order aberrations (or all aberration modes shown in Fig. 4) are corrected. Dashed line represents a Strehl ratio of 0.8, above which imaging is considered to be diffraction-limited.
Fig. 9
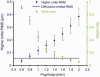
The total higher order aberration RMS increases, and the Strehl ratio decreases as the eye’s pupil size increases. Strehl ratio is calculated for the measurement wavelength of 789 nm. Diamond data points: average measured higher order RMS (3rd to 10th order) in µm. Dashed line: diffraction-limited RMS of λ/14, according to the Maréchal criterion. Triangular data points: average Strehl ratio for each pupil size. Error bars represent ± 2 SEM for the 20 eyes.
Fig. 10
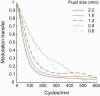
Mean of radial averaged MTF for 20 eyes over different pupil sizes (0.6 mm to 2 mm) for the measurement wavelength of 789 nm. Defocus and astigmatism are removed before MTF is calculated.
Fig. 11
Modulation transfers for a human eye (6 mm pupil) and a mouse eye (2 mm pupil) plotted in (a) cycles/degree to characterize angular resolution for vision and (b) cycles/mm to characterize spatial resolution for imaging the retina. Only higher order aberrations (HOA) are considered. Solid black line: mouse eye with 2 mm pupil size with HOA. Solid green line: human eye with 6 mm pupil size with HOA. Dashed black line: Diffraction-limited mouse eye with 2 mm pupil size. Dashed green line: Diffraction-limited human eye with 6 mm pupil size.
Fig. 12
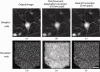
Simulated retinal images of ganglion cells and rod photoreceptors under ideal imaging conditions and in the absence of noise with/without AO correction. (a) A fluorescent ganglion cell image from a flat-mounted rat retina imaged with confocal microscopy with 1.2 NA. (b) A simulation of the retina in (a) being imaged without AO correction over a 0.8 mm pupil under the best possible condition. (c) A simulation of the same ganglion cell being imaged with AO correction over a 2 mm pupil under the best possible condition. (d) A simulated rod photoreceptor mosaic in the mouse retina. (e) & (f) are the same without AO and with AO simulations of the rod photoreceptor mosaic. Scale bar: 20 µm.
Fig. 13
Average modulation transfer functions for the mouse eye over a 0.8 mm pupil diameter. Note that MTFs are calculated for a wavelength of 514 nm, where rods and M-cones are near their spectral sensitivity peak.. To calculate MTF for a visible wavelength using wave aberration data measured at 789 nm, we assume other than defocus, variations in the other aberration coefficients between visible and IR wavelengths are small [26,56]. For all 20 eyes, defocus was increased by 7.9 D based on measured average LCA between the two wavelengths and Zernike coefficients for other aberrations remained the same.
Similar articles
- Optical aberrations in the mouse eye.
de la Cera EG, Rodríguez G, Llorente L, Schaeffel F, Marcos S. de la Cera EG, et al. Vision Res. 2006 Aug;46(16):2546-53. doi: 10.1016/j.visres.2006.01.011. Epub 2006 Mar 3. Vision Res. 2006. PMID: 16516259 - VioBio lab adaptive optics: technology and applications by women vision scientists.
Marcos S, Benedí-García C, Aissati S, Gonzalez-Ramos AM, Lago CM, Radhkrishnan A, Romero M, Vedhakrishnan S, Sawides L, Vinas M. Marcos S, et al. Ophthalmic Physiol Opt. 2020 Mar;40(2):75-87. doi: 10.1111/opo.12677. Epub 2020 Mar 8. Ophthalmic Physiol Opt. 2020. PMID: 32147855 Review. - Adaptive optics retinal imaging in the living mouse eye.
Geng Y, Dubra A, Yin L, Merigan WH, Sharma R, Libby RT, Williams DR. Geng Y, et al. Biomed Opt Express. 2012 Apr 1;3(4):715-34. doi: 10.1364/BOE.3.000715. Epub 2012 Mar 15. Biomed Opt Express. 2012. PMID: 22574260 Free PMC article. - Longitudinal chromatic aberration of the human eye in the visible and near infrared from wavefront sensing, double-pass and psychophysics.
Vinas M, Dorronsoro C, Cortes D, Pascual D, Marcos S. Vinas M, et al. Biomed Opt Express. 2015 Feb 24;6(3):948-62. doi: 10.1364/BOE.6.000948. eCollection 2015 Mar 1. Biomed Opt Express. 2015. PMID: 25798317 Free PMC article. - [Quantitative assessment of quality of vision].
Oshika T. Oshika T. Nippon Ganka Gakkai Zasshi. 2004 Dec;108(12):770-807; discussion 808. Nippon Ganka Gakkai Zasshi. 2004. PMID: 15656087 Review. Japanese.
Cited by
- In vivo volumetric analysis of retinal vascular hemodynamics in mice with spatio-temporal optical coherence tomography.
Węgrzyn P, Kulesza W, Wielgo M, Tomczewski S, Galińska A, Bałamut B, Kordecka K, Cetinkaya O, Foik A, Zawadzki RJ, Borycki D, Wojtkowski M, Curatolo A. Węgrzyn P, et al. Neurophotonics. 2024 Oct;11(4):0450031-4500322. doi: 10.1117/1.NPh.11.4.045003. Epub 2024 Oct 8. Neurophotonics. 2024. PMID: 39380716 Free PMC article. - Image metric-based multi-observation single-step deep deterministic policy gradient for sensorless adaptive optics.
Xu G, Smart TJ, Durech E, Sarunic MV. Xu G, et al. Biomed Opt Express. 2024 Jul 23;15(8):4795-4814. doi: 10.1364/BOE.528579. eCollection 2024 Aug 1. Biomed Opt Express. 2024. PMID: 39346980 Free PMC article. - Animal modeling for myopia.
Zheng L, Liao Z, Zou J. Zheng L, et al. Adv Ophthalmol Pract Res. 2024 Jun 5;4(4):173-181. doi: 10.1016/j.aopr.2024.06.001. eCollection 2024 Nov-Dec. Adv Ophthalmol Pract Res. 2024. PMID: 39263386 Free PMC article. Review. - The Parameters Governing the Anti-Myopia Efficacy of Chromatically Simulated Myopic Defocus in Tree Shrews.
She Z, Gawne TJ. She Z, et al. Transl Vis Sci Technol. 2024 May 1;13(5):6. doi: 10.1167/tvst.13.5.6. Transl Vis Sci Technol. 2024. PMID: 38722277 Free PMC article. - Multimodal photoacoustic microscopy, optical coherence tomography, and fluorescence imaging of USH2A knockout rabbits.
Nguyen VP, Hu J, Zhe J, Chen EY, Yang D, Paulus YM. Nguyen VP, et al. Sci Rep. 2023 Dec 12;13(1):22071. doi: 10.1038/s41598-023-48872-1. Sci Rep. 2023. PMID: 38086867 Free PMC article.
References
- Gray D. C., Merigan W., Wolfing J. I., Gee B. P., Porter J., Dubra A., Twietmeyer T. H., Ahamd K., Tumbar R., Reinholz F., Williams D. R., “In vivo fluorescence imaging of primate retinal ganglion cells and retinal pigment epithelial cells,” Opt. Express 14(16), 7144–7158 (2006).10.1364/OE.14.007144 - DOI - PubMed
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials