The evolution of antisocial punishment in optional public goods games - PubMed (original) (raw)
The evolution of antisocial punishment in optional public goods games
David G Rand et al. Nat Commun. 2011.
Abstract
Cooperation, where one individual incurs a cost to help another, is a fundamental building block of the natural world and human society. It has been suggested that costly punishment can promote the evolution of cooperation, with the threat of punishment deterring free-riders. Recent experiments, however, have revealed the existence of 'antisocial' punishment, where non-cooperators punish cooperators. While various theoretical models find that punishment can promote the evolution of cooperation, these models a priori exclude the possibility of antisocial punishment. Here we extend the standard theory of optional public goods games to include the full set of punishment strategies. We find that punishment no longer increases cooperation, and that selection favours substantial levels of antisocial punishment for a wide range of parameters. Furthermore, we conduct behavioural experiments, showing results consistent with our model predictions. As opposed to an altruistic act that promotes cooperation, punishment is mostly a self-interested tool for protecting oneself against potential competitors.
Figures
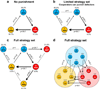
Figure 1. Using the full punishment strategy set, anti-social punishment is common and punishment does not promote cooperation
Time-averaged frequencies of each strategy and transition rates between homogeneous populations, (a) without punishment, (b) when cooperators can punish defectors, and (c,d) with the full set of punishment strategies. A strategy X-Y1Y2Y3 is defined by a public goods game action (X: C=cooperator, D=defector, L=loner), a punishment decision taken towards cooperators (Y1: N = no action, P = punish), defectors (Y2: N or P) and loners (Y3: N or P). Transition rates ρ are the probability that a new mutant goes to fixation multiplied by the population size. We indicate neutral drift (ρ = 1, dotted lines), slow transitions (ρ = 11.8, thin lines), intermediate transitions (ρ = 25.7, medium lines) and fast transitions (ρ = 38.7, thick lines). Transitions with rates less than 0.1 are not shown. Parameter values are N = 100, n = 5, r = 3, c = 1, γ = 0.3, β = 1 and σ = 1. In panels c and d, strategies which punish others taking the same public goods action are included in the analysis, but not pictured because they are strongly disfavored by selection and virtually non-existent in the steady state distribution. For clarity, transitions with ρ < 10 are not shown in panel d.
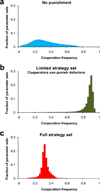
Figure 2. Robustness of results across parameter sets
Shown are the results of 100,000 numerical calculations using N = 100, n = 5, c = 1 and randomly sampling from uniform distributions on the intervals 1 < r < 5, 0 < σ < (_r_-1)c, 0 < γ < 5, and γ < β < 5γ. Results are shown for (a) the no-punishment strategy set, (b) the restricted punishment strategy set where only cooperators can punish loners, and (c) the full punishment strategy set.
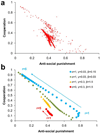
Figure 3. Inverse relationship between cooperation and anti-social punishment across parameters
(a) The steady state frequency of cooperation and anti-social punishment from 5,000 random parameter sets is shown. An inverse relationship is clearly visible: when antisocial punishment is rare, cooperation (and pro-social punishment) are common. (b) To explore this relationship, we vary r from (σ-c) to 5 for various values of σ, γ, and β, fixing N=100, n=5, and c=1. We see that increasing r always increases cooperation while decreasing anti-social punishment. We also see that when β is small, the range of cooperation and anti-social punishment values is large, whereas values are tightly constrained when β is larger. Achieving high levels of cooperation and low levels of anti-social punishment requires both large expected returns on public investment (large r) and symbolic punishments (small β).
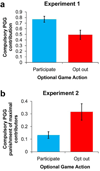
Figure 4. Two behavioral experiments are consistent with model predictions
(a) In Experiment 1, subjects play an optional public goods game followed by a compulsory public goods game. The average fraction contributed in the compulsory game is significantly lower among subjects who opt out of the optional game (Rank-sum, N=73, p=0.006). Thus as predicted, loners contribute less in compulsory games. (b) In Experiment 2, subjects play an optional game followed by a compulsory game with costly punishment. Subjects indicate how much (0, 1 or 2) they would punish each possible contribution level in the compulsory game. Subjects who opt out of the optional game invest significantly more in punishing those that contribute the maximal amount (Rank-sum, N=196, p=0.003). Thus as predicted, loners engage in more anti-social punishment. All games are one-shot interactions among 4 players, with contributions to the public good multiplied by 2. Punishment technology is 3:1. Results are robust to various controls and alternate methods of analysis; see Supplementary notes for details.
Similar articles
- Punishment does not promote cooperation under exploration dynamics when anti-social punishment is possible.
P Hauser O, A Nowak M, G Rand D. P Hauser O, et al. J Theor Biol. 2014 Nov 7;360:163-171. doi: 10.1016/j.jtbi.2014.06.041. Epub 2014 Jul 8. J Theor Biol. 2014. PMID: 25014473 - Stable polymorphism of cooperators and punishers in a public goods game.
Oya G, Ohtsuki H. Oya G, et al. J Theor Biol. 2017 Apr 21;419:243-253. doi: 10.1016/j.jtbi.2016.11.012. Epub 2016 Nov 21. J Theor Biol. 2017. PMID: 27880875 - Emergence of responsible sanctions without second order free riders, antisocial punishment or spite.
Hilbe C, Traulsen A. Hilbe C, et al. Sci Rep. 2012;2:458. doi: 10.1038/srep00458. Epub 2012 Jun 13. Sci Rep. 2012. PMID: 22701161 Free PMC article. - Cheating and punishment in cooperative animal societies.
Riehl C, Frederickson ME. Riehl C, et al. Philos Trans R Soc Lond B Biol Sci. 2016 Feb 5;371(1687):20150090. doi: 10.1098/rstb.2015.0090. Philos Trans R Soc Lond B Biol Sci. 2016. PMID: 26729930 Free PMC article. Review. - Punishment and spite, the dark side of cooperation.
Jensen K. Jensen K. Philos Trans R Soc Lond B Biol Sci. 2010 Sep 12;365(1553):2635-50. doi: 10.1098/rstb.2010.0146. Philos Trans R Soc Lond B Biol Sci. 2010. PMID: 20679108 Free PMC article. Review.
Cited by
- Evolutionary dynamics of group interactions on structured populations: a review.
Perc M, Gómez-Gardeñes J, Szolnoki A, Floría LM, Moreno Y. Perc M, et al. J R Soc Interface. 2013 Jan 9;10(80):20120997. doi: 10.1098/rsif.2012.0997. Print 2013 Mar 6. J R Soc Interface. 2013. PMID: 23303223 Free PMC article. - Egoistic punishment outcompetes altruistic punishment in the spatial public goods game.
Li J, Liu Y, Wang Z, Xia H. Li J, et al. Sci Rep. 2021 Mar 22;11(1):6584. doi: 10.1038/s41598-021-85814-1. Sci Rep. 2021. PMID: 33753774 Free PMC article. - The structure of mutations and the evolution of cooperation.
García J, Traulsen A. García J, et al. PLoS One. 2012;7(4):e35287. doi: 10.1371/journal.pone.0035287. Epub 2012 Apr 26. PLoS One. 2012. PMID: 22563381 Free PMC article. - Conditional punishment is a double-edged sword in promoting cooperation.
Huang F, Chen X, Wang L. Huang F, et al. Sci Rep. 2018 Jan 11;8(1):528. doi: 10.1038/s41598-017-18727-7. Sci Rep. 2018. PMID: 29323286 Free PMC article. - Evolution of prosocial punishment in unstructured and structured populations and in the presence of antisocial punishment.
Salahshour M. Salahshour M. PLoS One. 2021 Aug 6;16(8):e0254860. doi: 10.1371/journal.pone.0254860. eCollection 2021. PLoS One. 2021. PMID: 34358254 Free PMC article.
References
- Sigmund K. The calculus of selfishness. Princeton Univ Press; 2010.
- Ostrom E. Governing the commons: The evolution of institutions for collective action. Cambridge Univ Pr; 1990.
- Cressman R. The stability concept of evolutionary game theory: a dynamic approach. Springer-Verlag; 1992.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Research Materials