Hierarchical differentiation of myeloid progenitors is encoded in the transcription factor network - PubMed (original) (raw)

Hierarchical differentiation of myeloid progenitors is encoded in the transcription factor network

Jan Krumsiek et al. PLoS One. 2011.

Abstract

Hematopoiesis is an ideal model system for stem cell biology with advanced experimental access. A systems view on the interactions of core transcription factors is important for understanding differentiation mechanisms and dynamics. In this manuscript, we construct a Boolean network to model myeloid differentiation, specifically from common myeloid progenitors to megakaryocytes, erythrocytes, granulocytes and monocytes. By interpreting the hematopoietic literature and translating experimental evidence into Boolean rules, we implement binary dynamics on the resulting 11-factor regulatory network. Our network contains interesting functional modules and a concatenation of mutual antagonistic pairs. The state space of our model is a hierarchical, acyclic graph, typifying the principles of myeloid differentiation. We observe excellent agreement between the steady states of our model and microarray expression profiles of two different studies. Moreover, perturbations of the network topology correctly reproduce reported knockout phenotypes in silico. We predict previously uncharacterized regulatory interactions and alterations of the differentiation process, and line out reprogramming strategies.

PubMed Disclaimer

Conflict of interest statement

Competing Interests: The authors have declared that no competing interests exist.

Figures

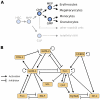
Figure 1

Figure 1. A regulatory model of myeloid differentiation.

(A) Hematopoietic stem cell (HSC) differentiation consists of a series of switch-like decisions. We here focus on differentiation into four myeloid cell types and omit other myeloid cells and the lymphoid branch (greyed out). For a detailed discussion of the different progenitor cell types, we refer the reader to . Abbreviations: MPP, multipotent progenitor; CMP, common myeloid progenitors; MEP, megakaryocyte-erythrocyte progenitor; GMP, granulocyte-monocyte progenitor; CLP, common lymphoid progenitor. (B) Literature-derived gene regulatory network for 11 myeloid players previously reported to be pivotal for the lineage decisions in myeloid differentiation (compare Text S1). Note that this visualization does not contain explicit Boolean update rules. Specifically, it is not apparent from the graph visualization alone whether multiple regulatory inputs are combined using AND or OR logic, which can make substantial differences for the resulting Boolean dynamics.

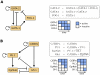
Figure 2

Figure 2. Functional modules in the network.

(A) The GATA-2, GATA-1, FOG-1 regulatory circuit consists of a coherent inhibitory feed-forward loop (GATA-1 and FOG-1 towards GATA-2), an autoregulation (by GATA-1) and a negative feedback (GATA-2 onto itself). The corresponding Boolean update rules and a schematic of the Boolean dynamics is shown on the right, demonstrating how the system is pushed towards maturation. GATA-2 activates its downstream target GATA-1, which synergizes with its cofactor FOG-1 to downregulate GATA-2. Due to the autoregulatory loop, GATA-1 can sustain its expression after its upstream regulator is inhibited. (B) Asymmetric activation of EgrNab and Gfi-1. The gene switch is driven by an upstream feed-forward loop around C/EBPformula image and PU.1. The Boolean update rules between the four players and two possible system trajectories are shown on the right. C/EBPformula image initially activates PU.1, but can also upregulate its antagonist Gfi-1 which then inhibits the PU.1 target EgrNab. Note that the two stable states - one where EgrNab is finally activated and one where Gfi-1 is activated - are mutually exclusive.

Figure 3

Figure 3. Systems dynamics of the myeloid differentiation model.

(A) State-transition graph of the Boolean model with dynamical trajectories. Each node represents a Boolean state of the system where each player is either ‘on’ or ‘off’. Each edge stands for a transition between two states induced by the application of a single Boolean update rule. The shown subgraph is calculated from an central early hematopoietic state and comprises 232 nodes with 789 links. The visualization emphasizes the existence of four attractors reachable from the early state, and the hierarchical structuring of the state space with two pairs of attractors (s1/s2 and s3/s4, respectively) that share a common attractor basin. The distance of a state from the attractor in the graph corresponds to the number of necessary update steps. (B) Interpretation of the state space in the context of myeloid differentiation. We observe a hierarchical partitioning with subsequent splits between the GM and MegE lineages, followed by splits of the granulocyte and monocyte lineages, and the erythrocyte and megakaryocyte lineages, respectively. Arrows in the diagram represent expression changes on the respective branch of the differentiation tree.

Figure 4

Figure 4. Comparison of Boolean states (top) with normalized mRNA expression profiles (bottom) for the 11 players of our model (see text for a detailed discussion).

We observe a good agreement between model prediction and measured mRNA expression. Note that we excluded non-differentially expressed genes with a maximum fold change smaller than 2 in all samples of the respective study (EgrNab in Pronk et al. and Fli-1 in Chambers et al. , greyed out). For a discussion of the mismatch between prediction and data for GATA-2, see main text.

Figure 5

Figure 5. In silico knockout experiments.

(A) Example case. When setting the expression value of PU.1 to zero in the model (left), a specific set of states becomes unreachable in the state space (right). In this case, these states correspond to the differentiation trajectories and attractors of the granulocytes and macrophage lineages. That is, functionally, we predict all myeloid progenitor cells to differentiate into the MegE lineage upon PU.1 knockout. (B) Knockout effects for all 11 players in our model. For each knockout we determined which of the original 4 attractors are still reachable and whether new attractors emerged. The ‘Comments’ column contains brief descriptions of the predicted effects on the differentiation process. In the ‘Evidence’ column we list publications that confirm the predictions of the respective in silico knockout , –, –.

Similar articles

Cited by

References

    1. Orkin SH, Zon LI. Hematopoiesis: an evolving paradigm for stem cell biology. Cell. 2008;132:631–644. - PMC - PubMed
    1. Cantor AB, Orkin SH. Hematopoietic development: a balancing act. Curr Opin Genet Dev. 2001;11:513–519. - PubMed
    1. Akashi K, Traver D, Miyamoto T, Weissman IL. A clonogenic common myeloid progenitor that gives rise to all myeloid lineages. Nature. 2000;404:193–197. - PubMed
    1. Iwasaki H, Akashi K. Myeloid lineage commitment from the hematopoietic stem cell. Immunity. 2007;26:726–740. - PubMed
    1. Mackey MC. 1997. pp. 149–178. The Art of Mathematical Modelling: Case Studies in Ecology, Physiology and Biouids, Prentice Hall, chapter Mathematical models of hematopoietic cell replication and control.

Publication types

MeSH terms

Substances

LinkOut - more resources