Statistics and truth in phylogenomics - PubMed (original) (raw)
Review
Statistics and truth in phylogenomics
Sudhir Kumar et al. Mol Biol Evol. 2012 Feb.
Abstract
Phylogenomics refers to the inference of historical relationships among species using genome-scale sequence data and to the use of phylogenetic analysis to infer protein function in multigene families. With rapidly decreasing sequencing costs, phylogenomics is becoming synonymous with evolutionary analysis of genome-scale and taxonomically densely sampled data sets. In phylogenetic inference applications, this translates into very large data sets that yield evolutionary and functional inferences with extremely small variances and high statistical confidence (P value). However, reports of highly significant P values are increasing even for contrasting phylogenetic hypotheses depending on the evolutionary model and inference method used, making it difficult to establish true relationships. We argue that the assessment of the robustness of results to biological factors, that may systematically mislead (bias) the outcomes of statistical estimation, will be a key to avoiding incorrect phylogenomic inferences. In fact, there is a need for increased emphasis on the magnitude of differences (effect sizes) in addition to the P values of the statistical test of the null hypothesis. On the other hand, the amount of sequence data available will likely always remain inadequate for some phylogenomic applications, for example, those involving episodic positive selection at individual codon positions and in specific lineages. Again, a focus on effect size and biological relevance, rather than the P value, may be warranted. Here, we present a theoretical overview and discuss practical aspects of the interplay between effect sizes, bias, and P values as it relates to the statistical inference of evolutionary truth in phylogenomics.
Figures
FIG. 1.
Anatomies of three types of phylogenomic data are discussed. (A) Genome-scale sequences for inferring evolutionary history of species, (B) a data set for tracing adaptive evolution for an individual codon, and (C) a multigene family sequence alignment for molecular phylogenetic analysis of gene duplications.
FIG. 2.
An illustration of how large data sets allow an arbitrarily great reduction in the variance of an estimate without making it any more accurate. Pairs of DNA sequences with an evolutionary distance of 0.7 substitutions per site were generated according to a GTR (Lanave et al. 1984; Tavare 1986) of evolution using SeqGen (Rambaut and Grassly 1997). The evolutionary distance between simulated sequences was then estimated under the JC model (Jukes and Cantor 1969). The JC model is a special case of GTR; it does not model transition/transversion bias or base frequency biases, both of which are present in the simulated data. Therefore, the distance estimates will be biased. The figure shows how the distribution of estimates derived from 1,000 replicates narrows with increasing number of sites used (100 to 10,000 bp for the sequence length, in steps of a factor of 10). Each distribution was approximately normal, so normal curves are shown for simplicity. The mean estimate of distance under the JC model is close to 0.62 in each case since an overly simple model tends to underestimate distances. At the same time, the distribution of estimated distances narrows with increasing sequence length as described by the central limit theorem. As a result, the apparent precision of the estimate improves with increasing sequence length, but this improvement is spurious, as the mean estimate remains incorrect because of violations of model assumptions. Indeed, as the sequence length increases, the distances become, in a sense, less truthful, as they converge to a biased value and away from the true one. Thus, our confidence in an incorrect estimate can become arbitrarily high when bias is involved.
FIG. 3.
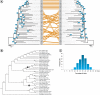
Examples based on evolutionary relationships of 33 mammals inferred using a set of 992 noncoding DNA sequence alignments of 1,000 bp each. (A) Comparison of trees inferred from two 1,000 bp genomic segments containing the fewest insertions and deletions (11.4% and 12.6%, respectively). Bootstrap support obtained from 5,000 replicates is shown for both segments. Phylogenetic trees were inferred using maximum composite likelihood distances under a Tamura–Nei model (Tamura, Nei, et al. 2004) for neighbor joining analysis (Saitou and Nei 1987) with MEGA software (Kumar et al. 2008). The two trees differ in many places, showing that a sequence length of 1,000 bp is insufficient to reliably estimate many mammalian evolutionary relationships. (B) An extended majority rule consensus tree based on the 960 ML phylogenies inferred under a GTR Model of nucleotide substitution with gamma distribution of rates and invariant sites (GTR+Γ+I); ML tree inference failed to converge/complete for 32 data sets. Numbers on branches refer to the percentage of data sets (trees) in which the indicated cluster in the consensus tree was observed. Although the consensus tree topology is quite similar to the nominal University of California at Santa Cruz (UCSC) mammalian tree, differing only in the position of the bats, the low consensus numbers show that individual segment trees differ extensively. (C) A histogram is depicted showing the distribution of the percent bases involved in insertions or deletions in the 992 UCSC alignments. The alignments were extracted from the hg18 human genome alignment available from the UCSC Genome Browser at
http://hgdownload.cse.ucsc.edu/goldenPath/hg18/multiz44way/
(Kuhn et al. 2009). Only the 32 placental and 1 marsupial species were used. We first divided each human chromosome into 1,000-bp segments and then all segments containing more than 600 sites with insertions and deletions for any placental or marsupial mammalian species in the alignment were discarded. This resulted in a total of 992 alignments of 1,000 bp each. I1 and I2 are two selected interior branches for which results are shown in figure 5.
FIG. 4.
Differences between the University of California at Santa Cruz (UCSC) tree of 32 placental mammals and neighbor joining (NJ) trees generated using five different sequence data partitions of similar size (first codon position, second codon position, third codon position, protein, and noncoding). The first three sets contain 83,407 bp, the protein set contains 83,407 amino acids, and the fifth data set consists of 100,000 noncoding DNA sites. The latter is a head-to-tail concatenation of 100 alignments of 1,000 bp homologous segments that have remained largely intact from insertions–deletions for the last 100 My (fewer than 20% of sites with an insertion or deletion). NJ trees were inferred using the maximum composite likelihood distance for DNA and the Jones–Taylor–Thornton substitution model for amino acids, respectively, in MEGA (Jones et al. 1992; Tamura et al. 2004; Kumar et al. 2008). Specific differences between the UCSC tree and the trees generated from different partitions are shown in the dotted boxes, along with bootstrap support values. Bootstrap support values for the main phylogeny (UCSC tree) were also calculated using 992,000 bp of noncoding DNA and were found to be 100% except for the two nodes flagged with a dagger (†), one of which had a bootstrap value of 82% (Perissodactyla as nearest neighbor to Carnivora) and the other of which (placement of bats as shown) was not present in the 992,000 bp tree.
FIG. 5.
Relationship of the interior branch lengths inferred from University of California at Santa Cruz (UCSC) database (Miller et al. 2007; Kuhn et al. 2009) and MUSCLE alignments for (A) external and (B) internal branches in the UCSC database phylogeny. Each point represents an average from the analysis of 992 data sets (1,000 bp each). For each data set, branch lengths were inferred by fitting the maximum composite likelihood distances onto the UCSC tree topology by employing the ordinary least squares (OLS) approach (Rzhetsky and Nei 1993) in MEGA5 (Tamura et al. 2011). The UCSC tree topology was created by Miller et al. (2007) as the one that seemed in best agreement with the published literature. OLS was chosen because it naturally allows for negative branch lengths that may occur when the topology used is not the optimal tree. MUSCLE alignments were conducted using the default options (Edgar 2004); UCSC generated alignments using the MULTIZ program (Blanchette et al. 2004) and the UCSC tree topology as described in detail in Miller et al. (2007). Histograms of differences between MUSCLE and UCSC branch lengths for individual 1,000 bp segment alignments are inset for two internal branches (I1 and I2), which show substantial difference in branch lengths between the UCSC and MUSCLE alignments. These two branches are marked by open circles in panel B scatter plot, and their positions in the UCSC phylogenetic tree are shown in figure 3_B_. Red bars in the histogram show the frequency of with which the use of segment-specific alignments produces smaller branch lengths than the UCSC alignment for the same segment.
Similar articles
- Mitochondrial phylogenomics of early land plants: mitigating the effects of saturation, compositional heterogeneity, and codon-usage bias.
Liu Y, Cox CJ, Wang W, Goffinet B. Liu Y, et al. Syst Biol. 2014 Nov;63(6):862-78. doi: 10.1093/sysbio/syu049. Epub 2014 Jul 28. Syst Biol. 2014. PMID: 25070972 - From cacti to carnivores: Improved phylotranscriptomic sampling and hierarchical homology inference provide further insight into the evolution of Caryophyllales.
Walker JF, Yang Y, Feng T, Timoneda A, Mikenas J, Hutchison V, Edwards C, Wang N, Ahluwalia S, Olivieri J, Walker-Hale N, Majure LC, Puente R, Kadereit G, Lauterbach M, Eggli U, Flores-Olvera H, Ochoterena H, Brockington SF, Moore MJ, Smith SA. Walker JF, et al. Am J Bot. 2018 Mar;105(3):446-462. doi: 10.1002/ajb2.1069. Epub 2018 May 8. Am J Bot. 2018. PMID: 29738076 - Phylogenomics of primates and their ancestral populations.
Siepel A. Siepel A. Genome Res. 2009 Nov;19(11):1929-41. doi: 10.1101/gr.084228.108. Epub 2009 Oct 3. Genome Res. 2009. PMID: 19801602 Free PMC article. - Phylogenomics.
Patané JSL, Martins J Jr, Setubal JC. Patané JSL, et al. Methods Mol Biol. 2018;1704:103-187. doi: 10.1007/978-1-4939-7463-4_5. Methods Mol Biol. 2018. PMID: 29277865 Review. - Genomes as documents of evolutionary history.
Boussau B, Daubin V. Boussau B, et al. Trends Ecol Evol. 2010 Apr;25(4):224-32. doi: 10.1016/j.tree.2009.09.007. Epub 2009 Oct 31. Trends Ecol Evol. 2010. PMID: 19880211 Review.
Cited by
- Untying the Gordian knot of plastid phylogenomic conflict: A case from ferns.
Wang T, Li TZ, Chen SS, Yang T, Shu JP, Mu YN, Wang KL, Chen JB, Xiang JY, Yan YH. Wang T, et al. Front Plant Sci. 2022 Nov 24;13:918155. doi: 10.3389/fpls.2022.918155. eCollection 2022. Front Plant Sci. 2022. PMID: 36507421 Free PMC article. - Evolution of the Highly Repetitive PEVK Region of Titin Across Mammals.
Muenzen K, Monroy J, Finseth FR. Muenzen K, et al. G3 (Bethesda). 2019 Apr 9;9(4):1103-1115. doi: 10.1534/g3.118.200714. G3 (Bethesda). 2019. PMID: 30804022 Free PMC article. - Simultaneous Bayesian estimation of alignment and phylogeny under a joint model of protein sequence and structure.
Herman JL, Challis CJ, Novák Á, Hein J, Schmidler SC. Herman JL, et al. Mol Biol Evol. 2014 Sep;31(9):2251-66. doi: 10.1093/molbev/msu184. Epub 2014 Jun 4. Mol Biol Evol. 2014. PMID: 24899668 Free PMC article. - Phylogenomics of strongylocentrotid sea urchins.
Kober KM, Bernardi G. Kober KM, et al. BMC Evol Biol. 2013 Apr 23;13:88. doi: 10.1186/1471-2148-13-88. BMC Evol Biol. 2013. PMID: 23617542 Free PMC article. - A beginner's guide to phylogenetics.
Sleator RD. Sleator RD. Microb Ecol. 2013 Jul;66(1):1-4. doi: 10.1007/s00248-013-0236-x. Epub 2013 Apr 28. Microb Ecol. 2013. PMID: 23624570 Review.
References
- Aguinaldo AM, Turbeville JM, Linford LS, Rivera MC, Garey JR, Raff RA, Lake JA. Evidence for a clade of nematodes, arthropods and other moulting animals. Nature. 1997;387:489–493. - PubMed
- Alfaro ME, Zoller S, Lutzoni F. Bayes or bootstrap? A simulation study comparing the performance of Bayesian Markov chain Monte Carlo sampling and bootstrapping in assessing phylogenetic confidence. Mol Biol Evol. 2003;20:255–266. - PubMed
- Anisimova M, Kosiol C. Investigating protein-coding sequence evolution with probabilistic codon substitution models. Mol Biol Evol. 2009;26:255–271. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources