Paired de bruijn graphs: a novel approach for incorporating mate pair information into genome assemblers - PubMed (original) (raw)
Paired de bruijn graphs: a novel approach for incorporating mate pair information into genome assemblers
Paul Medvedev et al. J Comput Biol. 2011 Nov.
Abstract
The recent proliferation of next generation sequencing with short reads has enabled many new experimental opportunities but, at the same time, has raised formidable computational challenges in genome assembly. One of the key advances that has led to an improvement in contig lengths has been mate pairs, which facilitate the assembly of repeating regions. Mate pairs have been algorithmically incorporated into most next generation assemblers as various heuristic post-processing steps to correct the assembly graph or to link contigs into scaffolds. Such methods have allowed the identification of longer contigs than would be possible with single reads; however, they can still fail to resolve complex repeats. Thus, improved methods for incorporating mate pairs will have a strong effect on contig length in the future. Here, we introduce the paired de Bruijn graph, a generalization of the de Bruijn graph that incorporates mate pair information into the graph structure itself instead of analyzing mate pairs at a post-processing step. This graph has the potential to be used in place of the de Bruijn graph in any de Bruijn graph based assembler, maintaining all other assembly steps such as error-correction and repeat resolution. Through assembly results on simulated perfect data, we argue that this can effectively improve the contig sizes in assembly.
Figures
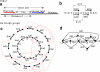
FIG. 1.
Mate pairs and the de Bruijn graph. (a) A mate pair is a pair of reads with a distance of d between their start positions. (b) A circular genome S and two mate pairs, with d = 4 and d = 5. (c, d) The de Bruijn graph construction for k = 2. (c) The outside circle shows a separate black edge for each 3-mer (equivalently, each element of the 3-spectrum). The dotted red lines indicate vertices that will be glued. The inner circle shows the result of applying some of the glues. Note that this is an intermediate step of the construction in which we only show the gluings of vertices arising from the same position of S. (d) The final de Bruijn graph, resulting from all the glues.
FIG. 2.
The effect of increasing k and d. (a) The number of repeated _k_-mers in the E. coli genome, for various values of k. (b) The number of repeated (k, d)-mers, for various values of d with k = 50.
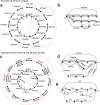
FIG. 3.
The (approximate) paired de Bruijn graph: (a, b) The paired de Bruijn construction for k = 2, d = 4 from the same string S as in Fig. 1. In (a), the outer circle has an edge from every element of the (3, 4)-spectrum. (b) The paired de Bruijn graph after all the gluings; notice that it has only one branching vertex, versus four in the de Bruijn graph (Fig. 1d). (c–e) The construction of the approximate paired de Bruijn graph for k = 2, d = 5, Δ = 1. In (c), one possible covering spectrum is shown in the outside circle, with black edges for elements with mate pair distance 6 and blue edges for distance 5. Since Δ = 1, we glue vertices if they have equal left labels and their right labels are a distance at most 2 apart from each other in the de Bruijn graph (Fig. 1d). The final multigraph after all vertex gluings is shown in (d), and the resulting simple graph, used to spell the contigs, is shown in (e). Notice that this graph now has three branching vertices.
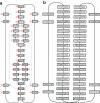
FIG. 4.
Example of the standard and paired de Bruijn graphs: The reads are the (5,12)-spectrum generated from the cyclic sequence ATCGGGATGACTATGTCGCTCCTAATCGGGAAGACTATGCCGCTCCTT. (a) The de Bruijn graph with edges constructed from the set of 5-mers in the (5,12) spectrum. Each node is a rectangle labeled by a 4-mer with the node ID shown as a large red number on the left of the node. The mate pair information is also presented in the graph: for each node, the node IDs of its corresponding right 4-mers are shown as small numbers on the right of the rectangle. For instance, the right 4-mers (blue dotted lines) of CGGG (node 3) are GTCG (node 21) and GCCG (node 22) and we write 21 and 22 on the right side of node 3. Note that there is not a single mate pair with a unique path between the mates, making mate pair transformations impossible. (b) The paired de Bruijn graph from the (5,12) spectrum is a cycle, representing a single contig. In this example, the paired approach allows for longer contigs than would mate pair transformations (though there are also examples when the opposite is true).
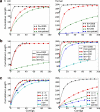
FIG. 5.
Contig lengths. Cumulative contig lengths (for standard and paired de Bruijn graphs) on simulated data with perfect coverage. Contigs are sorted in order from largest to smallest. Point (x, y) means the largest x contigs have cumulative length y. (a) To analyze the effect of the insert size (IS) on the assembly, we kept the read length fixed at 50, but varied the insert size. We also generated non-paired reads of length 50. For E. coli, the curve for insert size 6000 is not shown because there was only one contig, representing the whole genome. (b) To analyze the effect of read length on contig lengths, we fixed the insert size to 1000 but varied the read length. We also generated non-paired reads of length 1000, giving an upper bound on how good the assembly can be in this case. (c) To analyze the effect of variations in the insert size (Δ), we fixed the mean insert size (1000) and read length (50). We also show the baseline contig lengths in a non-paired dataset, with read length 50 and perfect coverage.
Similar articles
- Pathset graphs: a novel approach for comprehensive utilization of paired reads in genome assembly.
Pham SK, Antipov D, Sirotkin A, Tesler G, Pevzner PA, Alekseyev MA. Pham SK, et al. J Comput Biol. 2013 Apr;20(4):359-71. doi: 10.1089/cmb.2012.0098. Epub 2012 Jul 17. J Comput Biol. 2013. PMID: 22803627 Free PMC article. - FastEtch: A Fast Sketch-Based Assembler for Genomes.
Ghosh P, Kalyanaraman A. Ghosh P, et al. IEEE/ACM Trans Comput Biol Bioinform. 2019 Jul-Aug;16(4):1091-1106. doi: 10.1109/TCBB.2017.2737999. Epub 2017 Sep 11. IEEE/ACM Trans Comput Biol Bioinform. 2019. PMID: 28910776 - Read mapping on de Bruijn graphs.
Limasset A, Cazaux B, Rivals E, Peterlongo P. Limasset A, et al. BMC Bioinformatics. 2016 Jun 16;17(1):237. doi: 10.1186/s12859-016-1103-9. BMC Bioinformatics. 2016. PMID: 27306641 Free PMC article. - The present and future of de novo whole-genome assembly.
Sohn JI, Nam JW. Sohn JI, et al. Brief Bioinform. 2018 Jan 1;19(1):23-40. doi: 10.1093/bib/bbw096. Brief Bioinform. 2018. PMID: 27742661 Review. - Sequence assembly using next generation sequencing data--challenges and solutions.
Chin FY, Leung HC, Yiu SM. Chin FY, et al. Sci China Life Sci. 2014 Nov;57(11):1140-8. doi: 10.1007/s11427-014-4752-9. Epub 2014 Oct 17. Sci China Life Sci. 2014. PMID: 25326069 Review.
Cited by
- ExSPAnder: a universal repeat resolver for DNA fragment assembly.
Prjibelski AD, Vasilinetc I, Bankevich A, Gurevich A, Krivosheeva T, Nurk S, Pham S, Korobeynikov A, Lapidus A, Pevzner PA. Prjibelski AD, et al. Bioinformatics. 2014 Jun 15;30(12):i293-301. doi: 10.1093/bioinformatics/btu266. Bioinformatics. 2014. PMID: 24931996 Free PMC article. - A comparative analysis of methods for de novo assembly of hymenopteran genomes using either haploid or diploid samples.
Yahav T, Privman E. Yahav T, et al. Sci Rep. 2019 Apr 24;9(1):6480. doi: 10.1038/s41598-019-42795-6. Sci Rep. 2019. PMID: 31019201 Free PMC article. - Buffering updates enables efficient dynamic de Bruijn graphs.
Alanko J, Alipanahi B, Settle J, Boucher C, Gagie T. Alanko J, et al. Comput Struct Biotechnol J. 2021 Jul 6;19:4067-4078. doi: 10.1016/j.csbj.2021.06.047. eCollection 2021. Comput Struct Biotechnol J. 2021. PMID: 34377371 Free PMC article. - 2-kupl: mapping-free variant detection from DNA-seq data of matched samples.
Wang Y, Xue H, Pourcel C, Du Y, Gautheret D. Wang Y, et al. BMC Bioinformatics. 2021 Jun 5;22(1):304. doi: 10.1186/s12859-021-04185-6. BMC Bioinformatics. 2021. PMID: 34090332 Free PMC article. - Telescoper: de novo assembly of highly repetitive regions.
Bresler M, Sheehan S, Chan AH, Song YS. Bresler M, et al. Bioinformatics. 2012 Sep 15;28(18):i311-i317. doi: 10.1093/bioinformatics/bts399. Bioinformatics. 2012. PMID: 22962446 Free PMC article.
References
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources