The furrows of Rhinolophidae revisited - PubMed (original) (raw)
The furrows of Rhinolophidae revisited
Dieter Vanderelst et al. J R Soc Interface. 2012.
Abstract
Rhinolophidae, a family of echolocating bats, feature very baroque noseleaves that are assumed to shape their emission beam. Zhuang & Muller (Zhuang & Muller 2006 Phys. Rev. Lett. 97, 218701 (doi:10.1103/PhysRevLett.97.218701); Zhuang & Muller 2007 Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 76(Pt. 1), 051902 (doi:10.1103/PhysRevE.76.051902)) have proposed, based on finite element simulations, that the furrows present in the noseleaves of these bats act as resonance cavities. Using Rhinolophus rouxi as a model species, they reported that a resonance phenomenon causes the main beam to be elongated at a particular narrow frequency range. Virtually filling the furrows reduced the extent of the main lobe. However, the results of Zhuang & Muller are difficult to reconcile with the ecological background of R. rouxi. In this report, we replicate the study of Zhuang & Muller, and extend it in important ways: (i) we take the filtering of the moving pinnae into account, (ii) we use a model of the echolocation task faced by Rhinolophidae to estimate the effect of any alterations to the emission beam on the echolocation performance of the bat, and (iii) we validate our simulations using a physical mock-up of the morphology of R. rouxi. In contrast to Zhuang & Muller, we find the furrows to focus the emitted energy across the whole range of frequencies contained in the calls of R. rouxi (both in simulations and in measurements). Depending on the frequency, the focusing effect of the furrows has different consequences for the estimated echolocation performance. We argue that the furrows act to focus the beam in order to reduce the influence of clutter echoes.
Figures
Figure 1.
(a) Picture of Rhinolophus sinicus, a species closely related to Rhinolophus rouxi, showing the complex noseleaf structure, including the furrows. Photo courtesy of Garreth Jones, Bristol University. (b) A stylized spectrogram of the call of R. rouxi. (c) Renderings of the three-dimensional model of the complete head used to simulate the spatial hearing sensitivity of R. rouxi. (d) Rendering of the detailed model of the facial structure of R. rouxi. (e) A version of the three-dimensional model in which the upper two rows of furrows were filled as was performed by Zhuang & Muller [3,4] (see arrow). (f) Upper row: the simulated far field emission patterns for the original facial morphology (i.e. model in (d)). Middle row: far field simulated patterns for the model in which the furrows were filled (i.e. model in (e)). Bottom row: difference between upper and middle row.
Figure 2.
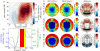
(a) The difference in echolocation performance between the model with open and filled furrows as a function of frequency and echo strength. Positive numbers (red colours) indicate that the performance of the model with filled furrows is better than the model with open furrows. (b) The blue line denotes the difference in echolocation performance between the model with filled and open furrows averaged across echo strengths (positive values indicate that the performance of the model with filled furrows is better than the model with open furrows). The green line denotes the difference in solid angle at half power (i.e. −3 dB) in the emission beam of both models (positive numbers indicate the beam of the model with the filled furrows is larger than the beam of the model with open furrows). The red and yellow bands in panel (b) depict the range of the frequency-modulated component and the constant frequency component, respectively, as given by Neuweiler et al. [8] (c) The entropy, i.e. the uncertainty about the origin of an echo, as a function of azimuth and elevation for both models as well as the difference between both models. The first row shows the entropy averaged across the whole range of modelled echo strengths at 75 kHz. The second row depicts the results for 25–35 dB only at 75 kHz. The bottom row shows the results for 37 kHz and a limited range of echo strengths (10–15 dB). In the difference plots, positive values (red colours) indicate that the performance of the model with filled furrows is better than the model with open furrows.
Similar articles
- The noseleaf of Rhinolophus formosae focuses the Frequency Modulated (FM) component of the calls.
Vanderelst D, Lee YF, Geipel I, Kalko EK, Kuo YM, Peremans H. Vanderelst D, et al. Front Physiol. 2013 Jul 19;4:191. doi: 10.3389/fphys.2013.00191. eCollection 2013. Front Physiol. 2013. PMID: 23882226 Free PMC article. - The aerodynamic cost of head morphology in bats: maybe not as bad as it seems.
Vanderelst D, Peremans H, Razak NA, Verstraelen E, Dimitriadis G. Vanderelst D, et al. PLoS One. 2015 Mar 4;10(3):e0118545. doi: 10.1371/journal.pone.0118545. eCollection 2015. PLoS One. 2015. PMID: 25739038 Free PMC article. - Interplay of lancet furrows and shape change in the horseshoe bat noseleaf.
Gupta AK, Webster D, Müller R. Gupta AK, et al. J Acoust Soc Am. 2015 Nov;138(5):3188-94. doi: 10.1121/1.4935387. J Acoust Soc Am. 2015. PMID: 26627792 - Neural maps for target range in the auditory cortex of echolocating bats.
Kössl M, Hechavarria JC, Voss C, Macias S, Mora EC, Vater M. Kössl M, et al. Curr Opin Neurobiol. 2014 Feb;24(1):68-75. doi: 10.1016/j.conb.2013.08.016. Epub 2013 Sep 17. Curr Opin Neurobiol. 2014. PMID: 24492081 Review. - Evolution of high duty cycle echolocation in bats.
Fenton MB, Faure PA, Ratcliffe JM. Fenton MB, et al. J Exp Biol. 2012 Sep 1;215(Pt 17):2935-44. doi: 10.1242/jeb.073171. J Exp Biol. 2012. PMID: 22875762 Review.
Cited by
- Intensity and directionality of bat echolocation signals.
Jakobsen L, Brinkløv S, Surlykke A. Jakobsen L, et al. Front Physiol. 2013 Apr 25;4:89. doi: 10.3389/fphys.2013.00089. eCollection 2013. Front Physiol. 2013. PMID: 23630501 Free PMC article. - Sensorimotor Model of Obstacle Avoidance in Echolocating Bats.
Vanderelst D, Holderied MW, Peremans H. Vanderelst D, et al. PLoS Comput Biol. 2015 Oct 26;11(10):e1004484. doi: 10.1371/journal.pcbi.1004484. eCollection 2015 Oct. PLoS Comput Biol. 2015. PMID: 26502063 Free PMC article. - The noseleaf of Rhinolophus formosae focuses the Frequency Modulated (FM) component of the calls.
Vanderelst D, Lee YF, Geipel I, Kalko EK, Kuo YM, Peremans H. Vanderelst D, et al. Front Physiol. 2013 Jul 19;4:191. doi: 10.3389/fphys.2013.00191. eCollection 2013. Front Physiol. 2013. PMID: 23882226 Free PMC article. - The aerodynamic cost of head morphology in bats: maybe not as bad as it seems.
Vanderelst D, Peremans H, Razak NA, Verstraelen E, Dimitriadis G. Vanderelst D, et al. PLoS One. 2015 Mar 4;10(3):e0118545. doi: 10.1371/journal.pone.0118545. eCollection 2015. PLoS One. 2015. PMID: 25739038 Free PMC article.
References
- Nowak R. M., Walker E. P. 1994. Walker's bats of the world. Baltimore, MD: Johns Hopkins University Press
- Schnitzler H. U., Grinnell A. 1977. Directional sensitivity of echolocation in the horseshoe bat, Rhinolophus ferrumequinum I. J. Comp. Physiol. A Neuroethol. Sens. Neural Behav. Physiol. 116, 51–6110.1007/BF00605516 (doi:10.1007/BF00605516) - DOI - DOI
- Zhuang Q., Muller R. 2006. Noseleaf furrows in a horseshoe bat act as resonance cavities shaping the biosonar beam. Phys. Rev. Lett. 97, 218701.10.1103/PhysRevLett.97.218701 (doi:10.1103/PhysRevLett.97.218701) - DOI - DOI - PubMed
- Zhuang Q., Muller R. 2007. Numerical study of the effect of the noseleaf on biosonar beamforming in a horseshoe bat. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 76(Pt. 1), 05190210.1103/PhysRevE.76.051902 (doi:10.1103/PhysRevE.76.051902) - DOI - DOI - PubMed
- Vanderelst D., De Mey F., Peremans H., Geipel I., Kalko E., Firzlaff U. 2010. What noseleaves do for FM bats depends on their degree of sensorial specialization. PLoS ONE 08, e1189310.1371/journal.pone.0011893 (doi:10.1371/journal.pone.0011893) - DOI - DOI - PMC - PubMed
MeSH terms
LinkOut - more resources
Full Text Sources