Inference of population structure using dense haplotype data - PubMed (original) (raw)

Inference of population structure using dense haplotype data

Daniel John Lawson et al. PLoS Genet. 2012 Jan.

Abstract

The advent of genome-wide dense variation data provides an opportunity to investigate ancestry in unprecedented detail, but presents new statistical challenges. We propose a novel inference framework that aims to efficiently capture information on population structure provided by patterns of haplotype similarity. Each individual in a sample is considered in turn as a recipient, whose chromosomes are reconstructed using chunks of DNA donated by the other individuals. Results of this "chromosome painting" can be summarized as a "coancestry matrix," which directly reveals key information about ancestral relationships among individuals. If markers are viewed as independent, we show that this matrix almost completely captures the information used by both standard Principal Components Analysis (PCA) and model-based approaches such as STRUCTURE in a unified manner. Furthermore, when markers are in linkage disequilibrium, the matrix combines information across successive markers to increase the ability to discern fine-scale population structure using PCA. In parallel, we have developed an efficient model-based approach to identify discrete populations using this matrix, which offers advantages over PCA in terms of interpretability and over existing clustering algorithms in terms of speed, number of separable populations, and sensitivity to subtle population structure. We analyse Human Genome Diversity Panel data for 938 individuals and 641,000 markers, and we identify 226 populations reflecting differences on continental, regional, local, and family scales. We present multiple lines of evidence that, while many methods capture similar information among strongly differentiated groups, more subtle population structure in human populations is consistently present at a much finer level than currently available geographic labels and is only captured by the haplotype-based approach. The software used for this article, ChromoPainter and fineSTRUCTURE, is available from http://www.paintmychromosomes.com/.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

Figure 1

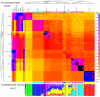
Figure 1. Illustration of the painting process to create the coancestry matrix.

We show the process by which a haplotype (haplotype 1, black) is painted using the others. A) True underlying genealogies for eight simulated sequences at three locations along a genomic segment, produced using the program ‘ms’ and showing coalescence times between haplotypes at each position. B) The Time to the Most Recent Common Ancestor (TMRCA) between haplotype 1 and each other haplotype, as a function of sequence position. Note multiple haplotypes can share the same TMRCA and changes in TMRCA correspond to historical recombination sites. C) True distribution of the ‘nearest neighbour’ haplotype. D) Sample ‘paintings’ of the Li & Stephens algorithm. E) Expectation of the painting process, estimating the nearest neighbour distribution. F) Resulting row of the coancestry matrix, based on the expectation of the painting.

Figure 2

Figure 2. Simulated data scenario and painting results.

A) Effective population size and B) population splits used for creating the simulated data. C) Coancestry heatmaps for linked and unlinked model with formula image regions and 20 individuals per population, showing formula image for (bottom left) the unlinked model, and (top right) the linked model; note that the linked heatmap is slightly asymmetric. D) PCA applied to the dataset using Eigenstrat on the raw SNP data. E) PCA on the coancestry matrix assuming markers are unlinked and F) linked (see text for details).

Figure 3

Figure 3. Simulated data population assignment results.

A) Pairwise coincidence matrix output by fineSTRUCTURE using chunk counts calculated using (top right) the linked and (bottom left) unlinked model, for the datasets from Figure 2C. The colouring represents the posterior coincidence probability (which does not drop below 97%) and the dots represent the maximum a posteriori (MAP) probability state. B) STRUCTURE-style ‘barplot’ for the results in A as well as ADMIXTURE results for the same dataset, where each colour represents a population (formula image, formula image and formula image respectively). C) Aggregated coancestry matrix (bottom left, normalized to have row mean 1) for the linked model dataset (top right) rescaled from Figure 2C (also top right), shown with the inferred MAP tree (top). D) Correlation with the truth as a function of the number of 5 Mb data regions for fineSTRUCTURE linked and unlinked models, and ADMIXTURE on the same data.

Figure 4

Figure 4. World HGDP results summary.

A) Relationship between populations for the whole world data. Each tip corresponds to a population; labels include the number of individuals and are coloured red if all individuals within that label are found in a single clade. See text for an interpretation of the values on the edges; the cut defines the ‘sub-continents’ discussed in the text. B) Transposed coancestry matrix for the Hazara and Burusho (in full: Figure S14), showing CentralSouthAsia and EastAsia donors, which are each normalised to have mean donation rate of 1. The box shows the ‘diagonal’ drift component.

Figure 5

Figure 5. Coancestry heat map for the Europe sub-continent.

A) (bottom left) population averages, (top right) the raw data matrix, and (left) chunks from other sub-continents. To symmetrise the matrices we show the average of the donor/recipient chunk counts; read the row and column for an individual to see their full profile. The tree has the same interpretation as Figure 4, and the heatmap between individuals in Europe has the same interpretation as Figure 2C, with extremely high (black) and low (white) values capped. Each continent has its own scale (top), with the lowest value in yellow and the highest in blue. B) ADMIXTURE barplot for the same dataset.

Figure 6

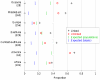
Figure 6. PCA for East Asia HGDP data.

The first 2 PCA components of the East Asian ‘continent’ as defined in Table S1 are shown for A) the linked model and B) the unlinked model. Only the named labels are displayed for clarity; Figure S37 shows the full set. Further structure will be present in other principal components (not shown).

Figure 7

Figure 7. Half-matching using correlations for HGDP data.

For each continent, we show the proportion of times in which two sets of chromosomes of a particular individual are matched correctly based on similarity of their coancestry profile. Coancestry profiles are calculated using a training set as described in the text. Results for coancestry matrices are calculated using correlation between individuals based on the linked and unlinked models. Also shown are the expected success in clustering if individuals within the same label or same inferred (linked results) fineSTRUCTURE population each had the same ancestry profile.

Similar articles

Cited by

References

    1. Menozzi P, Piazza A, Cavalli-Sforza L. Synthetic maps of human gene frequencies in europeans. Science. 1978;201:786–792. - PubMed
    1. Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155:945–959. - PMC - PubMed
    1. Novembre J, Stephens M. Interpreting principal component analyses of spatial population genetic variation. Nature Genetics. 2008;40:646–649. - PMC - PubMed
    1. McVean G. A Genealogical Interpretation of Principal Components Analysis. PLoS Genet. 2009;5:e1000686. doi: 10.1371/journal.pgen.1000686. - DOI - PMC - PubMed
    1. Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, et al. Principal components analysis corrects for stratification in genome-wide association studies. Nature Genetics. 2006;38:904–909. - PubMed

Publication types

MeSH terms

LinkOut - more resources