Summarizing and correcting the GC content bias in high-throughput sequencing - PubMed (original) (raw)

Summarizing and correcting the GC content bias in high-throughput sequencing

Yuval Benjamini et al. Nucleic Acids Res. 2012 May.

Abstract

GC content bias describes the dependence between fragment count (read coverage) and GC content found in Illumina sequencing data. This bias can dominate the signal of interest for analyses that focus on measuring fragment abundance within a genome, such as copy number estimation (DNA-seq). The bias is not consistent between samples; and there is no consensus as to the best methods to remove it in a single sample. We analyze regularities in the GC bias patterns, and find a compact description for this unimodal curve family. It is the GC content of the full DNA fragment, not only the sequenced read, that most influences fragment count. This GC effect is unimodal: both GC-rich fragments and AT-rich fragments are underrepresented in the sequencing results. This empirical evidence strengthens the hypothesis that PCR is the most important cause of the GC bias. We propose a model that produces predictions at the base pair level, allowing strand-specific GC-effect correction regardless of the downstream smoothing or binning. These GC modeling considerations can inform other high-throughput sequencing analyses such as ChIP-seq and RNA-seq.

PubMed Disclaimer

Figures

Figure 1.

Figure 1.

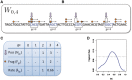
Single position model estimation. (A) Mappable positions along the genome are randomly sampled (⇓); (B) these positions are stratified by the GC count in the corresponding sliding window (here a = 0, l = 4); (C) the number of fragments (→) with 5′-end (○) in sampled locations are counted; (D) mean fragment rates for each stratum are estimated, taking the ratio between fragment count and positions in the stratum. These form the GC curve (here the curve for a = 75, l = 50 from Figure 4C).

Figure 2.

Figure 2.

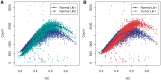
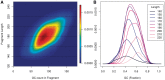
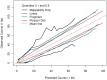
GC curves (10 kb bins). Observed fragment counts and loess lines plotted against GC of (A) two libraries from the same normal sample, and (B) the tumor library (red) with its matched normal sample library (blue). Counts and curves of all libraries are scaled to fit median counts of normal library 1. Bins were randomly sampled from chromosome 1, and counts include fragments from both strands.

Figure 3.

Figure 3.

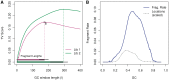
Single position models. (A) The top curves represent TV scores for GC windows of different lengths, all beginning at 0 (a = 0). The horizontal bars on the bottom mark the median fragment lengths (and 0.05, 0.95 quantiles). For each library, the strongest GC windows are those that encompass the full fragment. For library 1, we mark the optimal model (_W_0,180), and show its resulting GC curve on the right panel (B). (We actually show _W_2,176, removing 2 bp from each side of the fragment.) The GC curve measures the fragment rate given the fraction of GC in the window. Vertical lines (blue) represent 1 SD. For comparison, we plot the distribution of GC (dotted line) in our sample from chromosome 1 (scaled).

Figure 4.

Figure 4.

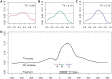
Different lags. (A) GC curve of the window before the fragment, _W_−50,50; (B) within the read, _W_0,50 and (C) in the fragment center, not overlapping the read, _W_75,50. (D) A plot of TV scores for 50 bp sliding windows (W a,50). The _x_-axis marks a, the location of the window 5′-end relative to 5′-end of the fragment. On the bottom, we mark a fragment and its reads in relation to the GC windows from the top panels.

Figure 5.

Figure 5.

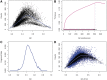
Fragment rate by length and GC. (A) A heat map describes rates for each (GC, length) pair. Each dotted line represents a single length. In (B), GC curves for fragments of specific lengths are drawn [corresponding to the dotted lines in (A)]. Blue / dark curves represent shorter fragments than red / bright. Here _x_-axis is the fraction of GC. All fragment length models here have a margin of 2 from both fragment ends (a = 2, m = 2).

Figure 6.

Figure 6.

Fragmentation effect. Left: relative abundance of nucleotides at fixed positions relative to fragment 5′-end. A horizontal dotted line marks the relative abundance of the base at mappable positions. Right: fragment rates when stratifying by the dinucleotide (−1,0). Dinucleotide counts overlapping the fragment 5′-end.

Figure 7.

Figure 7.

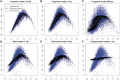
Aggregation of single location estimates. (A–C) Estimates based on the fragment GC curve (black) trace similar paths as loess (cyan) estimated on observed counts (blue) on multiple scales. (D–F) Estimates based on alternative models compared with observed counts on 1 kb bins. (D) Read model, predictions based on GC of the 5′ read only (_W_0,75); (E) Two-ended model uses GC (30 bp) from both ends of the fragments; (F) Fragmentation model based on location-specific composition around the 5′-end. See

Supplementary methods

for details on how models for (E) and (F) were defined and estimated.

Figure 8.

Figure 8.

Corrected counts of normal sample. (A) Counts in 1 kb bins not corrected for GC (top), corrected by loess (center) and corrected by fragment model (bottom), positions 58 000–62 000 kb of chromosome 1 (chr1). (B) Histograms of the corrected counts (random sample of 1 kb bins in chr1). Each point represents counts from both libraries (forward strand).

Figure 9.

Figure 9.

CN gain from tumor sample. Counts and corrected counts at position 29 000 kb on chromosome 2. (A) Unnormalized counts at 1 kb bins (top), corrected by loess (center) and corrected by fragment model (bottom). GC curves estimated on chromosome 1 (which has no large CN changes). (B) Histogram of normalized counts at 28–30 mb (underlined on left plots).

Figure 10.

Figure 10.

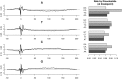
Comparison to Poisson variation. 0.1 and 0.9 quantiles of observed counts grouped by estimated rates. Models that predict better will have narrower vertical spreads. Variation around the mean of the fragment model (green), the loess (blue) and mappability (black) are compared to variation around a Poisson (red).

Figure 11.

Figure 11.

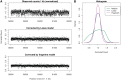
GC plots for Dataset 2. (A) GC effect for 10 kb (chromosome 1). (B) TV scores for GC windows of different lengths with a = 0 (comparable to Figure 3). (C) GC curve at fragment model (_W_2,500). (D) Observed (blue) and predicted (black) counts against GC for 10 kb bins (chromosome 2).

Similar articles

Cited by

References

    1. Dohm JC, Lottaz C, Borodina T, Himmelbauer H. Substantial biases in ultra-short read data sets from high-throughput DNA sequencing. Nucleic Acids Res. 2008;36:e105. - PMC - PubMed
    1. Chiang DY, Getz G, Jaffe DB, O'Kelly MJ, Zhao X, Carter SL, Russ C, Nusbaum C, Meyerson M, Lander ES. High-resolution mapping of copy-number alterations with massively parallel sequencing. Nat. Methods. 2008;6:99–103. - PMC - PubMed
    1. Quail MA, Kozarewa I, Smith F, Scally A, Stephens PJ, Durbin R, Swerdlow H, Turner DJ. A large genome center's improvements to the Illumina sequencing system. Nat. Methods. 2008;5:1005–1010. - PMC - PubMed
    1. Ivakhno S, Royce T, Cox AJ, Evers DJ, Cheetham RK, Tavaré S. CNAseg—a novel framework for identification of copy number changes in cancer from second-generation sequencing data. Bioinformatics. 2010;26:3051. - PubMed
    1. Yoon S, Xuan Z, Makarov V, Ye K, Sebat J. Sensitive and accurate detection of copy number variants using read depth of coverage. Genome Res. 2009;19:1586. - PMC - PubMed

Publication types

MeSH terms

Substances

LinkOut - more resources