Revisiting the isobole and related quantitative methods for assessing drug synergism - PubMed (original) (raw)
Review
Revisiting the isobole and related quantitative methods for assessing drug synergism
Ronald J Tallarida. J Pharmacol Exp Ther. 2012 Jul.
Abstract
The isobole is well established and commonly used in the quantitative study of agonist drug combinations. This article reviews the isobole, its derivation from the concept of dose equivalence, and its usefulness in providing the predicted effect of an agonist drug combination, a topic not discussed in pharmacology textbooks. This review addresses that topic and also shows that an alternate method, called "Bliss independence," is inconsistent with the isobolar approach and also has a less clear conceptual basis. In its simplest application the isobole is the familiar linear plot in cartesian coordinates with intercepts representing the individual drug potencies. It is also shown that the isobole can be nonlinear, a fact recognized by its founder (Loewe) but neglected or rejected by virtually all other users. Whether its shape is linear or nonlinear the isobole is equally useful in detecting synergism and antagonism for drug combinations, and its theoretical basis leads to calculations of the expected effect of a drug combination. Numerous applications of isoboles in preclinical testing have shown that synergism or antagonism is not only a property of the two agonist drugs; the dose ratio is also important, a fact of potential importance to the design and testing of drug combinations in clinical trials.
Figures
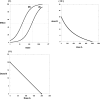
Fig. 1.
I, dose-effect curves for agonists with a constant potency ratio (10:1) with ED50 values of 200 and 20. II, the isobole for the 50% effect is linear, has intercepts equal to the respective ED50 values, and obeys the equation a/200 + b/20 = 1 for doses a and b. All points (a,b) on the isobole represent dose pairs that are expected to give effect = 50% _E_max when there is no interaction between the drugs. III, if the maximal effects _E_A and _E_B differ (say, _E_A = 60 and _E_B = 100), the potency ratio is not constant and the isobole, for the usual hyperbolic dose-effect curves, is nonlinear and given by the equation (Grabovsky and Tallarida, 2004):
where _C_A is the dose of drug A that gives effect ½ _E_A. For dose-effect curves with slopes that differ this result is easily generalized as discussed in Grabovsky and Tallarida (2004) and Tallarida (2006, .
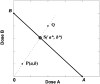
Fig. 2.
Shown here is a linear isobole with an observed synergistic point P having coordinates (a,b), the additive point S with coordinates (a*,b*), and a subadditive point Q. The broken radial line denotes the dose combinations in a fixed ratio. In this case of a linear isobole the interaction index, denoted T, is calculated from the coordinates of P as T = a/A + b/B, a value less than unity and therefore indicative of synergism. For this case (linear isobole) it also follows that T is the ratio of radial distances 0P/0S, which also equals the ratio of total doses, (a + b)/(a* + b*). Situations of suspected departures from additivity require statistical testing of the difference (observed total − additive total). The variance (square of S.E.) for the additive total _Z_add is given by
The S.E. of the observed total dose is obtained from the dose-effect data of the combination. These totals and their S.E. are examined as the difference as described previously (Tallarida, 2000).
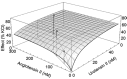
Fig. 3.
Shown is a response surface for the effect of two vasoconstrictors on isolated aortic rings, where the effect is expressed as the percentage of tension produced by KCl. Three dose combinations in the fixed ratio 94:6 were tested and showed that the two highest doses produced effects above the additive surface. Based on Lamarre and Tallarida (2008) with permission.
Similar articles
- Drug Combinations: Tests and Analysis with Isoboles.
Tallarida RJ. Tallarida RJ. Curr Protoc Pharmacol. 2016 Mar 18;72:9.19.1-9.19.19. doi: 10.1002/0471141755.ph0919s72. Curr Protoc Pharmacol. 2016. PMID: 26995550 Free PMC article. - An overview of drug combination analysis with isobolograms.
Tallarida RJ. Tallarida RJ. J Pharmacol Exp Ther. 2006 Oct;319(1):1-7. doi: 10.1124/jpet.106.104117. Epub 2006 May 2. J Pharmacol Exp Ther. 2006. PMID: 16670349 - The application of drug dose equivalence in the quantitative analysis of receptor occupation and drug combinations.
Tallarida RJ, Raffa RB. Tallarida RJ, et al. Pharmacol Ther. 2010 Aug;127(2):165-74. doi: 10.1016/j.pharmthera.2010.04.011. Epub 2010 May 28. Pharmacol Ther. 2010. PMID: 20546783 Free PMC article. Review. - Fitting models for the joint action of two drugs using SAS.
Whitehead A, Whitehead J, Todd S, Zhou Y, Smith MK. Whitehead A, et al. Pharm Stat. 2008 Oct-Dec;7(4):272-84. doi: 10.1002/pst.312. Pharm Stat. 2008. PMID: 17979217 - Dose addition and the isobole method as approaches for predicting the cumulative effect of non-interacting chemicals: a critical evaluation.
Bosgra S, van Eijkeren JC, Slob W. Bosgra S, et al. Crit Rev Toxicol. 2009;39(5):418-26. doi: 10.1080/10408440902787592. Crit Rev Toxicol. 2009. PMID: 19514914 Review.
Cited by
- Identification of optimal dosing schedules of dacomitinib and osimertinib for a phase I/II trial in advanced EGFR-mutant non-small cell lung cancer.
Poels KE, Schoenfeld AJ, Makhnin A, Tobi Y, Wang Y, Frisco-Cabanos H, Chakrabarti S, Shi M, Napoli C, McDonald TO, Tan W, Hata A, Weinrich SL, Yu HA, Michor F. Poels KE, et al. Nat Commun. 2021 Jun 17;12(1):3697. doi: 10.1038/s41467-021-23912-4. Nat Commun. 2021. PMID: 34140482 Free PMC article. Clinical Trial. - Evaluation of synergism in drug combinations and reference models for future orientations in oncology.
Duarte D, Vale N. Duarte D, et al. Curr Res Pharmacol Drug Discov. 2022 May 12;3:100110. doi: 10.1016/j.crphar.2022.100110. eCollection 2022. Curr Res Pharmacol Drug Discov. 2022. PMID: 35620200 Free PMC article. Review. - Behavioral effects of triazolam and pregnanolone combinations: reinforcing and sedative-motor effects in female rhesus monkeys.
Cook JE, Platt DM, Rüedi-Bettschen D, Rowlett JK. Cook JE, et al. Front Psychiatry. 2023 May 12;14:1142531. doi: 10.3389/fpsyt.2023.1142531. eCollection 2023. Front Psychiatry. 2023. PMID: 37252149 Free PMC article. - A military-centered approach to neuroprotection for traumatic brain injury.
Shear DA, Tortella FC. Shear DA, et al. Front Neurol. 2013 Jun 12;4:73. doi: 10.3389/fneur.2013.00073. eCollection 2013. Front Neurol. 2013. PMID: 23781213 Free PMC article. - Using Various Nonlinear Response Surfaces for Mathematical Description of the Type of Combined Toxicity.
Varaksin AN, Panov VG, Katsnelson BA, Minigalieva IA. Varaksin AN, et al. Dose Response. 2018 Dec 5;16(4):1559325818816596. doi: 10.1177/1559325818816596. eCollection 2018 Oct-Dec. Dose Response. 2018. PMID: 30574029 Free PMC article.
References
- Adams JU, Tallarida RJ, Geller EB, Adler MW. (1993) Isobolographic superadditivity between δ and μ opioid agonists in the rat depends on the ratio of compounds, the μ agonist and the analgesic assay used. J Pharmacol Exp Ther 266:1261–1267 - PubMed
- Berenbaum MC. (1989) What is synergy? Pharmacol Rev 41:93–141 - PubMed
- Bliss CI. (1939) The toxicity of poisons applied jointly. Ann Appl Biol 26:585–615
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources