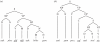Artificial grammar learning meets formal language theory: an overview - PubMed (original) (raw)
Review
Artificial grammar learning meets formal language theory: an overview
W Tecumseh Fitch et al. Philos Trans R Soc Lond B Biol Sci. 2012.
Abstract
Formal language theory (FLT), part of the broader mathematical theory of computation, provides a systematic terminology and set of conventions for describing rules and the structures they generate, along with a rich body of discoveries and theorems concerning generative rule systems. Despite its name, FLT is not limited to human language, but is equally applicable to computer programs, music, visual patterns, animal vocalizations, RNA structure and even dance. In the last decade, this theory has been profitably used to frame hypotheses and to design brain imaging and animal-learning experiments, mostly using the 'artificial grammar-learning' paradigm. We offer a brief, non-technical introduction to FLT and then a more detailed analysis of empirical research based on this theory. We suggest that progress has been hampered by a pervasive conflation of distinct issues, including hierarchy, dependency, complexity and recursion. We offer clarifications of several relevant hypotheses and the experimental designs necessary to test them. We finally review the recent brain imaging literature, using formal languages, identifying areas of convergence and outstanding debates. We conclude that FLT has much to offer scientists who are interested in rigorous empirical investigations of human cognition from a neuroscientific and comparative perspective.
Figures
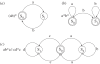
Figure 1.
Three examples of simple finite-state automata and their stringsets. Circles represent states, arcs represent transitions between states, with the corresponding symbols, and double circles indicate ‘accept’ states. (a) The (ab)* or (ab)n: accepts strings of zero or more ‘ab’ bigrams. (b) The a*b*: accepts any number of ‘a's followed by any number of ‘b's. (c) A long-distance dependency: this automaton illustrates that FSAs can also check for arbitrarily long-distance dependencies. This grammar accepts strings of the form ab*a, where any number of ‘b's can intervene between the two ‘dependent’ ‘a's, (or similarly for cd*c strings).
Figure 2.
The Chomsky hierarchy for grammars, languages and automata. The Chomsky hierarchy is an inclusion hierarchy that aligns particular forms of grammar, and the languages they generate, with particular classes of automata—abstract computational ‘machines’ that can be constructed to accept such languages. All of the grey circles beyond the innermost white circle represent the supra-regular grammars and languages, which require computational power above the level of a finite-state automaton. See Jäger & Rogers [16] for more details.
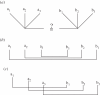
Figure 3.
Three possible strategies, and corresponding structures, for recognizing A_n_B_n_. (a) The simplest strategy is ‘count-and-compare’: count the number of ‘a's and the number of ‘b's, and then accept the string if they are equal. This strategy is supra-regular, and generates a single hierarchical level. (b) An alternative strategy yields a ‘nested’ or ‘centre-embedded’ structure, and is a natural strategy for a pushdown automaton because it matches each ‘b’ with the most recently seen ‘a’. (c) A third strategy yields a ‘crossed’ dependency, and cannot be accomplished with a single pushdown stack. It thus requires at least a context-sensitive grammar.
Figure 4.
Regular string supersets for A_n_B_n_. Although recognition of the specific stringset A_n_B_n_ requires a supra-regular grammar, various regular languages contain A_n_B_n_ strings as special cases. For example, the regular language A*B* includes all strings of ‘A's followed by ‘B's, including those where the number happens to be the same. Similarly, the regular language {A,B}* simply means ‘any string of ‘A's and ‘B's’ and also obviously includes A_n_B_n_ strings as a special case. Thus, perhaps non-intuitively, the most inclusive languages (the outer circles of the figure) require less powerful computational machinery.
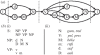
Figure 5.
Artificial grammar of BROCANTO. (a) Transition from the left to the right following the arrows generates a sentence. For example, {dN Vm DMN}, {dDMN v} and {dN v dN} are correct sentences generated from this automaton. The nodes represent syntactic categories: N (noun), d and D (determiner), v (verb), M (adjective) and m (adverb), and ‘[’ and ‘]’ represents the start and end symbols. (b) The rewriting rules (i) of the grammar. The rules define the derivation of S (sentence), NP (noun phrase) and VP (verb phrase) from the terminal symbols given as a set of novel vocabulary (ii).
Figure 6.
Phrase structures for modified version of BROCANTO. BROCANTO was modified to investigate the difference between grammars that have long-distance dependency (indicated by underlined element (a,b)) and those that do not. Moreover, the introduction of the complementizer required a word order change in the subordinate clause: from (a) verb second position in the main clause to (b) verb final position in the subordinate clause. (a) Structure with local dependencies. Dependent elements are underlined. (b) Structure with long-distance dependencies. Dependent elements are underlined. A set of rewriting rules builds a hierarchical structure. The rewriting rules are represented as binary branches, e.g. S → NP VP. S, sentence; NP, noun phrase; VP, verb phrase; CP, complementizer phrase; D, determiner; A, adjective; N, noun; V, verb; M, verb modifier; C, complementizer.
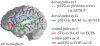
Figure 7.
Structural connectivities between the language cortices. Schematic of two dorsal pathways and two ventral pathways. Dorsal pathway I connects the superior temporal gyrus (STG) to the premotor cortex via the arcuate fasiculus (AF) and the superior longitudinal fasiculus (SLF). Dorsal pathway II connects the STG to BA 44 via the AF/SLF. Ventral pathway I connects BA 45 and the temporal cortex via the extreme capsule fibre system (ECFS). Ventral pathway II connects the frontal operculum (FOP) and the anterior temporal STG/STS via the uncinate fasciculus (UF). Reproduced from Friederici [91].
Similar articles
- Pattern perception and computational complexity: introduction to the special issue.
Fitch WT, Friederici AD, Hagoort P. Fitch WT, et al. Philos Trans R Soc Lond B Biol Sci. 2012 Jul 19;367(1598):1925-32. doi: 10.1098/rstb.2012.0099. Philos Trans R Soc Lond B Biol Sci. 2012. PMID: 22688630 Free PMC article. - Formal language theory: refining the Chomsky hierarchy.
Jäger G, Rogers J. Jäger G, et al. Philos Trans R Soc Lond B Biol Sci. 2012 Jul 19;367(1598):1956-70. doi: 10.1098/rstb.2012.0077. Philos Trans R Soc Lond B Biol Sci. 2012. PMID: 22688632 Free PMC article. Review. - Toward a computational framework for cognitive biology: unifying approaches from cognitive neuroscience and comparative cognition.
Fitch WT. Fitch WT. Phys Life Rev. 2014 Sep;11(3):329-64. doi: 10.1016/j.plrev.2014.04.005. Epub 2014 May 13. Phys Life Rev. 2014. PMID: 24969660 Review. - Computational and evolutionary aspects of language.
Nowak MA, Komarova NL, Niyogi P. Nowak MA, et al. Nature. 2002 Jun 6;417(6889):611-7. doi: 10.1038/nature00771. Nature. 2002. PMID: 12050656 Review. - Discovery of a Recursive Principle: An Artificial Grammar Investigation of Human Learning of a Counting Recursion Language.
Cho PW, Szkudlarek E, Tabor W. Cho PW, et al. Front Psychol. 2016 Jun 8;7:867. doi: 10.3389/fpsyg.2016.00867. eCollection 2016. Front Psychol. 2016. PMID: 27375543 Free PMC article.
Cited by
- Far transfer of retrieval-practice benefits: rule-based learning as the underlying mechanism.
Opitz B, Kubik V. Opitz B, et al. Cogn Res Princ Implic. 2024 Oct 8;9(1):65. doi: 10.1186/s41235-024-00598-y. Cogn Res Princ Implic. 2024. PMID: 39379748 Free PMC article. - Artificial Grammar Learning Capabilities in an Abstract Visual Task Match Requirements for Linguistic Syntax.
Westphal-Fitch G, Giustolisi B, Cecchetto C, Martin JS, Fitch WT. Westphal-Fitch G, et al. Front Psychol. 2018 Jul 24;9:1210. doi: 10.3389/fpsyg.2018.01210. eCollection 2018. Front Psychol. 2018. PMID: 30087630 Free PMC article. - Universal Grammar and Biological Variation: An EvoDevo Agenda for Comparative Biolinguistics.
Benítez-Burraco A, Boeckx C. Benítez-Burraco A, et al. Biol Theory. 2014;9(2):122-134. doi: 10.1007/s13752-014-0164-0. Epub 2014 Mar 15. Biol Theory. 2014. PMID: 24955079 Free PMC article. - EEG potentials associated with artificial grammar learning in the primate brain.
Attaheri A, Kikuchi Y, Milne AE, Wilson B, Alter K, Petkov CI. Attaheri A, et al. Brain Lang. 2015 Sep;148:74-80. doi: 10.1016/j.bandl.2014.11.006. Epub 2014 Dec 17. Brain Lang. 2015. PMID: 25529405 Free PMC article. - Cellular computation and cognition.
Fitch WT. Fitch WT. Front Comput Neurosci. 2023 Nov 23;17:1107876. doi: 10.3389/fncom.2023.1107876. eCollection 2023. Front Comput Neurosci. 2023. PMID: 38077750 Free PMC article.
References
- Turing A. M. 1936–1937 On computable numbers, with an application to the Entscheidungsproblem. Proc. Lond. Math. Soc. 42, 230–265
- Post E. L. 1944. Recursively enumerable sets of positive integers and their decision problems. Bull. Am. Math. Soc. 50, 284–31610.1090/S0002-9904-1944-08111-1 (doi:10.1090/S0002-9904-1944-08111-1) - DOI - DOI
- Chomsky N. 1956. Three models for the description of language. IRE Trans. Inf. Theory IT-2, 113–12410.1109/TIT.1956.1056813 (doi:10.1109/TIT.1956.1056813) - DOI - DOI
- Chomsky N. 1959. On certain formal properties of grammars. Inf. Control 2, 137–16710.1016/S0019-9958(59)90362-6 (doi:10.1016/S0019-9958(59)90362-6) - DOI - DOI
- Hopcroft J. E., Motwani R., Ullman J. D. 2000. Introduction to automata theory, languages and computation, 2nd edn Reading, MA: Addison-Wesley
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous