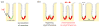Spatial structure increases the waiting time for cancer - PubMed (original) (raw)

Spatial structure increases the waiting time for cancer

Erik A Martens et al. New J Phys. 2011.

Abstract

Cancer results from a sequence of genetic and epigenetic changes which lead to a variety of abnormal phenotypes including increased proliferation and survival of somatic cells, and thus, to a selective advantage of pre-cancerous cells. The notion of cancer progression as an evolutionary process has been experiencing increasing interest in recent years. Many efforts have been made to better understand and predict the progression to cancer using mathematical models; these mostly consider the evolution of a well-mixed cell population, even though pre-cancerous cells often evolve in highly structured epithelial tissues. In this study, we propose a novel model of cancer progression that considers a spatially structured cell population where clones expand via adaptive waves. This model is used to assess two different paradigms of asexual evolution that have been suggested to delineate the process of cancer progression. The standard scenario of periodic selection assumes that driver mutations are accumulated strictly sequentially over time. However, when the mutation supply is sufficiently high, clones may arise simultaneously on distinct genetic backgrounds, and clonal adaptation waves interfere with each other. We find that in the presence of clonal interference, spatial structure increases the waiting time for cancer, leads to a patchwork structure of non-uniformly sized clones, decreases the survival probability of virtually neutral (passenger) mutations, and that genetic distance begins to increase over a characteristic length scale L(c). These characteristic features of clonal interference may help to predict the onset of cancers with pronounced spatial structure and to interpret spatially-sampled genetic data obtained from biopsies. Our estimates suggest that clonal interference likely occurs in the progression of colon cancer, and possibly other cancers where spatial structure matters.

PubMed Disclaimer

Figures

Figure 1

Figure 1

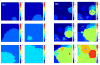
Two important dynamical regimes may dominate clonal expansions: Periodic selection (a): Mutations occur so rarely that adaptive (clonal) waves sweep through the habitat one-by-one. Clonal interference (b): Frequent mutations lead to simultaneous competition of clones, which collide at a characteristic “interference” length Lc. In the presence of such clonal interference, only few clones may reach fixation, leading to the loss of clones carrying a selective advantage, thus slowing down evolution [26, 27]. Simulations were carried out on a hexagonal lattice with side length L = 100 and absorbing boundary conditions with a selective advantage of _s_0 = 0.25 and a mutation rate of μ = 10−7 in (a), and μ = 10−5 in (b). The interference length is determined via Eq. (4) and is Lc ~ 29 for periodic selection and Lc ~ 135 for clonal interference, respectively. Selective advantages are drawn from an exponential distribution. Small numbers denotes the time sequence. Colors define different levels of (logarithmic) fitness.

Figure 2

Figure 2

Clonal expansion is possible via crypt bifurcation, and has been observed in the human colon [11, 32] and may play an important role in Barrett’s esophagus [10]. Mutations can occur anywhere within the epithelium but persist only in stem cells. The number ν of stem cells in a crypt is very small. A mutation can spread in the stem cells until most stem cells within the crypt carry that mutation (a). At some point, crypts go through a bifurcation process (b). Such processes continue throughout the life of the host. If the mutation is pro-oncogenic, it may lead to a higher proliferation rate and to the spreading of potentially cancerous mutations over several crypts in the neoplasm. Crypts have an orifice width δ and are relatively densely packed, with an average spacing Δ.

Figure 3

Figure 3

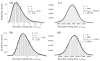
The (rescaled) waiting times for k hits, tk/_t_mut, (histogram bars) for small and large neoplasm sizes L. When the neoplasm size is small (a,b), clones reach fixation one-by-one. In this case of periodic selection, waiting times are distributed according to Eq. (2) (solid curve). Larger neoplasms increase the mutation supply rate, _μL_2, and shorten the typical waiting time for successful mutations to occur, _t_mut = (2_s_0_μL_2)−1. When the neoplasm size is sufficiently large (c,d), mutations arise frequently and their clones interfere at a characteristic interference length Lc, given by Eq. (4). However, in this case of clonal interference (c,d), waiting times are normally distributed (solid curve; see text). Data represents 1000 realizations with exponentially distributed fitness effects with mean _s_0 = 0.05 and mutation rate μ = 10−4 per crypt and cycle, yielding an interference length of Lc ~ 17, in agreement with our estimates for colon cancer (Table 1).

Figure 4

Figure 4

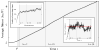
The logarithmic fitness 〈log W (t)〉, averaged over the entire crypt population (lattice sites), increases at a constant average rate _v_·_s_0 after a transient time τ (see Ref. [27]). At this point, the number of coexisting clones also starts to saturate (left inset). After the saturated state, the accumulation rate carries out a random walk (right inset) around its mean value v (dashed red line), given by Eq. (6), resulting in the Gaussian distribution of waiting times seen in Fig. 3(c,d). The relative width of the Gaussian distribution of waiting times scales like σ/〈_tk_〉 ~ (v/k)1/2, see Eq. (8). Vertical dashed lines denote the times at which k = 5, 10, 20 hits have been acquired. The simulation is carried out with _s_0 = 0.05, μ = 10−3 (corresponding to a characteristic interference length Lc ~ 8) and a neoplasm size L = 100, until k = 20 hits have occurred.

Figure 5

Figure 5

The average waiting time for the accumulation of k = 5 and k = 10 driver mutations is associated with the waiting time for cancer. For periodic selection (L < Lc), the rate-limiting step is for both well-mixed and spatially extended populations given by the waiting time for the next successful mutation _t_mut. The waiting time is thus 〈_tk_〈 = k · _t_mut (the mismatch in the data for non-structured and structured populations is due to the finite size effects for small neoplasm sizes). For clonal interference, the waiting time for k hits is markedly longer for spatially structured (black) than non-structured populations (red). The discrepancy between non-structured and spatially structured populations increases for larger number of driver mutations k. Error bars indicate the sample standard deviations σ(tk). The inset displays how the relative (sample) standard deviation σ(tk)/〈_tk_〉 depends on the neoplasm size L. Notice that fluctuations around the mean are smaller in the clonal interference than in the periodic selection regime (see inset). Simulations were carried out with absorbing boundaries and exponentially distributed selective advantages. We have chosen a selective advantage of _s_0 = 0.05 and a mutation rate of μ = 10−4, such that the characteristic interference length Lc ~ 17 falls into the range of values we have estimated for pre-malignant tissues in the colon (see Table 1).

Figure 6

Figure 6

Distribution of rescaled clonal patch sizes after k = 5 and k = 10 hits have occurred (clonal interference). The patch size A is defined as the number of crypts carrying the same mutation. The mean clonal patch size is of order Lc2. Data represents 1000 realizations with a neoplasm width of L = 1000, exponentially distributed selective advantages with mean _s_0 = 0.05, and a mutation rate of μ = 10−4 (yielding an interference length of Lc ~ 17, in agreement with estimates in Table 1). Clonal patches of 1 are excluded, since the patch at the end of the simulation always has size 1, thus generating an unrealistic bias.

Figure 7

Figure 7

Genetic (Hamming) distance (number of differing mutations in two crypts) increases as a function of spatial distance over the characteristic interference scale Lc (for clonal interference). The genetic distance g(r) in the figure represents the average genetic distances found within a radial interval [r, r + Δ_r_[with binning width Δ_r_ = 1, and is calculated after k = 5 (a) or k = 10 (b) hits have occurred. Each curve represents the ensemble average over 100 realizations; standard errors are too small to be seen on this plot. Simulations were carried out for neoplasms with side length L = 316, exponentially distributed selective fitness effects with mean _s_0 = 0.05, mutation rates μ = 10−4, 10−3, 10−2 per crypt and a crypt cycle, corresponding to Lc ~ 4, 8, 18.

Figure 8

Figure 8

Distribution of fitness effects of mutations in the terminating (“winning”) clone with k = 5 and k = 10 hits. For periodic selection (L = 5), the shape of the fitness distribution is similar to the exponential distribution from which effects are drawn during the simulation (a); no significant difference is discernible in the fitness distribution for non-structured (blue) and structured populations (red). However, when clones interfere (L = 1000), the following observations are made (panels (b) and (c)): (i) the mean 〈_s_〉 is larger, demonstrating that (ii) almost neutral mutations are less likely to survive than for periodic selection, and (iii) distributions for non-structured and spatially structured populations have markedly different shapes: the distribution of fitness effects exhibits a distinct bimodal structure for the spatially structured case, and the associated mean selective advantage is approximately twice as large as in the non-structured population. 500 Simulations have been carried out with selective fitness effects drawn from an exponential distribution with mean _s_0 = 0.05 and a mutation rate of μ = 10−4 (i.e. Lc ~ 17, in agreement with our estimates for colonic tissue in Table 1).

Similar articles

Cited by

References

    1. Nowell PC. The clonal evolution of tumor cell populations. Science. 1976;194:23–28. - PubMed
    1. Tsao J-L, Yatabe Y, Salovaara R, Järvinen HJ, Mecklin J-P, Aaltonen LA, Tavaré S, Shibata D. Genetic reconstruction of individual colorectal tumor histories. Proc Nat Ac Sci. 2000;97:1236–1241. - PMC - PubMed
    1. Gonzalez-Garcia I, Sole RV, Costa J. Metapopulation dynamics and spatial heterogeneity in cancer. Proc Nat Ac Sci. 2002;99:13085–9. - PMC - PubMed
    1. Maley CC, Galipeau PC, Finley JC, Wongsurawat VJ, Li X, Sanchez C, Paulson TG, Blount PL, Risques R-A, Rabinovitch PS, Reid BJ. Genetic clonal diversity predicts progression to esophageal adenocarcinoma. Nature Genetics. 2006 Apr;38(4):468–73. - PubMed
    1. Beerenwinkel N, Antal T, Dingli D, Traulsen A, Kinzler KW, Velculescu VE, Vogelstein B, Nowak MA. Genetic progression and the waiting time to cancer. PLoS Computational Biology. 2007 Nov;3(11):e225. - PMC - PubMed

LinkOut - more resources