Length distributions of identity by descent reveal fine-scale demographic history - PubMed (original) (raw)

Length distributions of identity by descent reveal fine-scale demographic history

Pier Francesco Palamara et al. Am J Hum Genet. 2012.

Erratum in

Abstract

Data-driven studies of identity by descent (IBD) were recently enabled by high-resolution genomic data from large cohorts and scalable algorithms for IBD detection. Yet, haplotype sharing currently represents an underutilized source of information for population-genetics research. We present analytical results on the relationship between haplotype sharing across purportedly unrelated individuals and a population's demographic history. We express the distribution of IBD sharing across pairs of individuals for segments of arbitrary length as a function of the population's demography, and we derive an inference procedure to reconstruct such demographic history. The accuracy of the proposed reconstruction methodology was extensively tested on simulated data. We applied this methodology to two densely typed data sets: 500 Ashkenazi Jewish (AJ) individuals and 56 Kenyan Maasai (MKK) individuals (HapMap 3 data set). Reconstructing the demographic history of the AJ cohort, we recovered two subsequent population expansions, separated by a severe founder event, consistent with previous analysis of lower-throughput genetic data and historical accounts of AJ history. In the MKK cohort, high levels of cryptic relatedness were detected. The spectrum of IBD sharing is consistent with a demographic model in which several small-sized demes intermix through high migration rates and result in enrichment of shared long-range haplotypes. This scenario of historically structured demographies might explain the unexpected abundance of runs of homozygosity within several populations.

Copyright © 2012 The American Society of Human Genetics. Published by Elsevier Inc. All rights reserved.

PubMed Disclaimer

Figures

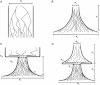
Figure 1

Figure 1

Demographic Models (A) Population of constant size. (B) Exponential expansion (contraction for

N a > N c

). (C) A founder event followed by exponential expansion. (D) Two subsequent exponential expansions divided by a founder event.

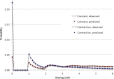
Figure 2

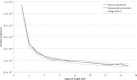
Figure 2

Distribution of Total Sharing The theoretically predicted distribution of total IBD (dots) is compared to the one observed in simulations (dashed lines) for two demographic scenarios: a constant population of 2,000 diploid individuals (red) and an exponentially contracting population in which 50,000 ancestral individuals are reduced to 500 current individuals over 20 generations (blue). For the constant-population model, the distribution was computed for IBD segments in the length interval

R = [1, 4]

, whereas all segments of at least 1 cM were considered for the exponential contraction. The empirical distribution was estimated from the comparison of 124,750 haploid pairs (250 synthetic diploid individuals), whereas the theoretical distribution was predicted with Equation 17. The analyzed genomic region has a length of ∼278 cM, and the distributions were discretized with intervals of 0.1 cM.

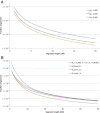
Figure 3

Figure 3

Effects of Demographic Parameters on IBD Sharing When a population of constant size N e is considered (A), a larger number of individuals in the population results in a decreased chance of sharing IBD segments across all length intervals. A similar behavior is observed for the case of an exponential population expansion (B) parameterized by N a ancestral individuals exponentially expanding to N c current individuals during G generations. Larger values of N a and N c correspond to a smaller chance of IBD sharing for short and long segments, respectively. For fixed N a and N c, changes in G (affecting the expansion rate) have an impact on segments of medium length, i.e., the slope of the distribution between short and long segments.

Figure 4

Figure 4

Performance of the Inference Procedure Performance for constant-size populations (A), expanding and contracting populations (B), and a suddenly expanding population (C) studied with a constant-size model (D). (A) We generated synthetic populations of size ranging from 500–40,000 individuals. The ratio between true (x axis) and estimated (y axis) population size has a median of 1.00 and a 95% CI of 0.97–1.03. (B) When expanding and contracting populations were simulated across a wide range of demographic parameters (see Table S1), the reconstructed population size at any of the recent generations (blue dots) was within 10% of the true size 95% of the time. Higher uncertainty was observed in the most recent generations (black lines indicate generation-specific 95% CIs). (C) Demographic model for instantaneous expansion. N a ancestral individuals suddenly expand to N c individuals G generations before the present. (D) We simulated several populations by using the model in (C); we set

N a = 1, 500

and

N c = 25, 000

and used different values for G. We analyzed the demography of this population by assuming a constant-sized population model and used IBD segments in several length intervals to infer the population size. When inference is performed on the basis of longer IBD segments, the prediction is quicker to converge to the current population size when the time from expansion is increased. For example, expansions that occurred more than 100 generations ago leave a negligible signature when IBD segments between 4 and 5 cM in length are considered (purple). An inference procedure based on average levels of heterozygosity, which is strongly biased by population size at ancient times, provides little insight into recent demography even for extremely old expansion events (dark green). In all cases, we simulated a realistic chromosome 1 for 500 diploid samples, equivalent to ∼140 diploid individuals analyzed genome wide.

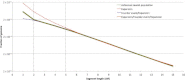
Figure 5

Figure 5

Reconstruction for the AJ Demographic History We applied several demographic models to study the demographic history of 500 self-reported AJ individuals on the basis of the observed distribution of haplotype sharing (green line). The parameters of exponential expansion can be optimized to provide a good fit when only long (≥5 cM) segments are considered (red line, Figure 1B; best fit:

N c ∼ 97, 700, 000

, G = 26, and

N a ∼ 1, 300

). However, this model is not flexible enough to accommodate abundant short segments found in this population. The milder slope observed between segments of 2–5 cM in length suggests a larger ancestral population size that rapidly recovered from a severe founder event by expanding to reach a large modern population size (purple line, Figure 1C; best-fit:

N c ∼ 12, 800, 000, G = 35, N _a_1 ∼ 230, and N _a_2 ∼ 70, 600).

Still, this model cannot provide a good fit for additional slope variation (observed for segments between 1–2 cM) that is well explained by an additional exponential expansion that precedes the founder event but that is distinct from the other, more recent expansion (orange line; Figure 1D; best-fit:

N c ∼ 42, 000, 000, _G_1 = 33, N _a_1 ∼ 23, N _a_2 ∼ 37, 800, N _a_3 ∼ 1, 800, and _G_2 = 167

). All population sizes are expressed as diploid individuals. _G_2 was not optimized because it was assumed that

_G_1 + _G_2 = 200

.

Figure 6

Figure 6

MKK Demography IBD sharing is high across MKK samples, particularly for long haplotypes. Our analysis of the observed distribution of haplotype sharing (red) with the use of a single-population model (blue) suggests occurrence of a severe population contraction in recent generations (∼23,500 ancestral individuals decreasing to ∼500 current individuals during 23 generations at a high exponential rate r ∼ −0.17). An alternative demographic model containing several small demes that interact through high migration rates creates the same effect as a recent severe population bottleneck and provides and alternative justification to the abundance and distribution of IBD sharing. In particular, we reconstructed a plausible scenario (dashed CI obtained through random resampling of 200 synthetic data sets) in which 44 villages of 485 individuals each intermix with a migration rate of 0.13 per individual per generation.

Similar articles

Cited by

References

    1. Bamshad M., Wooding S.P. Signatures of natural selection in the human genome. Nat. Rev. Genet. 2003;4:99–111. - PubMed
    1. Freedman M.L., Reich D., Penney K.L., McDonald G.J., Mignault A.A., Patterson N., Gabriel S.B., Topol E.J., Smoller J.W., Pato C.N. Assessing the impact of population stratification on genetic association studies. Nat. Genet. 2004;36:388–393. - PubMed
    1. Wall J.D. Detecting ancient admixture in humans using sequence polymorphism data. Genetics. 2000;154:1271–1279. - PMC - PubMed
    1. Wall J.D., Hammer M.F. Archaic admixture in the human genome. Curr. Opin. Genet. Dev. 2006;16:606–610. - PubMed
    1. Li H., Durbin R. Inference of human population history from individual whole-genome sequences. Nature. 2011;475:493–496. - PMC - PubMed

Publication types

MeSH terms

LinkOut - more resources