A complex network framework for unbiased statistical analyses of DNA-DNA contact maps - PubMed (original) (raw)
A complex network framework for unbiased statistical analyses of DNA-DNA contact maps
Kai Kruse et al. Nucleic Acids Res. 2013 Jan.
Abstract
Experimental techniques for the investigation of three-dimensional (3D) genome organization are being developed at a fast pace. Currently, the associated computational methods are mostly specific to the individual experimental approach. Here we present a general statistical framework that is widely applicable to the analysis of genomic contact maps, irrespective of the data acquisition and normalization processes. Within this framework DNA-DNA contact data are represented as a complex network, for which a broad number of directly applicable methods already exist. In such a network representation, DNA segments and contacts between them are denoted as nodes and edges, respectively. Furthermore, we present a robust method for generating randomized contact networks that explicitly take into account the inherent 3D nature of the genome and serve as realistic null-models for unbiased statistical analyses. By integrating a variety of large-scale genome-wide datasets we demonstrate that meiotic crossover sites display enriched genomic contacts and that cohesin-bound genes are significantly colocalized in the yeast nucleus. We anticipate that the complex network framework in conjunction with the randomization of DNA-DNA contact networks will become a widely used tool in the study of nuclear architecture.
Figures
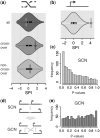
Figure 1.
Data normalization and filtering, complex network framework and topological network properties (a) Log2 contact enrichment of yeast inter-chromosomal DNA–DNA contact data (11) before and after normalization using the probabilistic model of Yaffe and Tanay (15). (b) Filtering of contacts. (c) The high-confidence map of filtered DNA–DNA contacts is represented as a complex network. (d) Randomized networks that maintain essential properties of the original. (e) A large number of random networks is generated using the procedure suggested in this study. (f–h) Topological analysis of the yeast inter-chromosomal segment contact network (SCN). Green denotes yeast SCN nodes, grey denotes random networks of the same size and degree sequence as the yeast SCN (‘rewired networks’, not to be confused with the randomization approach). (f) Degree distribution. (g) Average clustering coefficient distribution. (h) Average clustering coefficient distribution for mixed triangles (where two nodes are neighbours on the same chromosome).
Figure 2.
Colocalization assessment in DNA–DNA contact networks. (a) Colocalization assessment using our randomization approach, in direct comparison to the resampling approach (
Supplementary Materials and Methods
). Green nodes are the nodes investigated for colocalization. Rectangular nodes correspond to the nodes investigated in each of the random null-models. (b) Colocalization assessment tests for 250 random sets of 100 nodes in each of 50 artificial SCNs (Materials and Methods section). Grey (background): rewired random networks (no correction of clustering), excess of low _P_-values (arrow). Green (foreground): randomization approach. (c, d) Boxplots of node degrees in the above-mentioned sets binned by colocalization _P_-value for the resampling approach (light-grey) and the randomization approach (green), respectively. _P_-values obtained by Wilcoxon rank-sum test. Outliers have been omitted for clarity. (e) Boxplots showing that the degree of nodes in the SCN is dependent on the corresponding segment-lengths. Segments have been binned according to their degree into four categories, where 0 is unconnected, while low, med and high are formed by the first, second + third and fourth quartile of nodes, respectively. _P_-value calculated using the Wilcoxon rank-sum test (f) Schematic of colocalized nodes with low versus high degrees.
Figure 3.
Colocalization assessment results of randomization approach in the yeast SCN and GCN. (a) Meiotic recombination hotspot contact enrichment. Figure shows the distribution of contact counts in the randomized networks in comparison to the contact count between recombination hotspots in the original network (violin plot = combined density- and boxplot), measured by the SPI. (b) ORF colocalization (c, e) _P_-value distribution from the colocalization assessment of 1000 gene subsets of 250 genes each. (c) Yeast SCN. Skew towards low _P_-values is clearly visible. (d) Schematic showing the SCN to GCN (gene contact network) conversion (e) Yeast GCN. Skew towards low _P_-values is no longer visible.
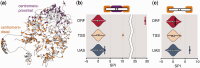
Figure 4.
Cohesin subunit IRR1p colocalization (a) Cohesin binding sites at the UAS overlaid on a 3D representation of the budding yeast genome (11). (b, c) Violinplots of SPIs for IRR1p-bound genes in random networks. SPI of original contact count indicated by rectangle and horizontal line. One plot for each of the three datasets (ORF, TSS and UAS). (b) SPIs of full dataset—note the broken axis between SPI 10 and 25. (c) SPIs of centromere-distal IRR1p-bound genes.
Figure 5.
Unbiased randomization procedure for DNA–DNA contact networks. Our randomization approach for DNA–DNA contact networks aims at maintaining the defining network properties of the original network, thereby creating an appropriate ‘null-model’ for comparison. The toy example illustrates the effects of each randomization step at the network and the DNA level (in a 2D representation). Step 1: This ‘rewiring’ part of the randomization procedure shuffles the contacts between DNA segments by selecting pairs of edges and swapping their targets. While this maintains the exact degrees of every node, the number of triangles is significantly reduced, essentially disrupting the strong clustering behaviour. Thus, no compact representation exists for the rewired network. Step 2: To correct the long-range clustering behaviour, triangles are introduced into the rewired network by an established Markov-chain procedure (31), until the transitivity T (the ratio of observed triangles to possible triangles in the network) of the random network matches that of the original network _T_orig. Step 3: Since the number of ‘mixed triangles’ (where two of the participating nodes are not connected by an edge, but are neighbours on the same chromosome) is also decreased in the rewired networks, this step increases the corresponding mixed transitivity _T_′ until it matches the original mixed transitivity _T_′orig in the same fashion as Step 2. Step 3 is optional, especially in colocalization assessment, because it will only have an effect if genes or DNA segments of interest are actually chromosomal neighbours. In Steps 2 and 3, the overall clustering behaviour is restored, however, individual nodes are allowed to vary in their clustering behaviour. See
Supplementary Figure S9
for comparison of rewired and fully randomized networks.
Similar articles
- In vitro assembly of physiological cohesin/DNA complexes.
Onn I, Koshland D. Onn I, et al. Proc Natl Acad Sci U S A. 2011 Jul 26;108(30):12198-205. doi: 10.1073/pnas.1107504108. Epub 2011 Jun 13. Proc Natl Acad Sci U S A. 2011. PMID: 21670264 Free PMC article. - Genome-wide mapping of the cohesin complex in the yeast Saccharomyces cerevisiae.
Glynn EF, Megee PC, Yu HG, Mistrot C, Unal E, Koshland DE, DeRisi JL, Gerton JL. Glynn EF, et al. PLoS Biol. 2004 Sep;2(9):E259. doi: 10.1371/journal.pbio.0020259. Epub 2004 Jul 27. PLoS Biol. 2004. PMID: 15309048 Free PMC article. - SMC complexes differentially compact mitotic chromosomes according to genomic context.
Schalbetter SA, Goloborodko A, Fudenberg G, Belton JM, Miles C, Yu M, Dekker J, Mirny L, Baxter J. Schalbetter SA, et al. Nat Cell Biol. 2017 Sep;19(9):1071-1080. doi: 10.1038/ncb3594. Epub 2017 Aug 21. Nat Cell Biol. 2017. PMID: 28825700 Free PMC article. - The Yeast Genomes in Three Dimensions: Mechanisms and Functions.
Noma KI. Noma KI. Annu Rev Genet. 2017 Nov 27;51:23-44. doi: 10.1146/annurev-genet-120116-023438. Epub 2017 Aug 30. Annu Rev Genet. 2017. PMID: 28853923 Review. - Cohesin: a guardian of genome integrity.
Mehta GD, Rizvi SM, Ghosh SK. Mehta GD, et al. Biochim Biophys Acta. 2012 Aug;1823(8):1324-42. doi: 10.1016/j.bbamcr.2012.05.027. Epub 2012 Jun 5. Biochim Biophys Acta. 2012. PMID: 22677545 Review.
Cited by
- Improving 3D Genome Reconstructions Using Orthologous and Functional Constraints.
Diament A, Tuller T. Diament A, et al. PLoS Comput Biol. 2015 May 22;11(5):e1004298. doi: 10.1371/journal.pcbi.1004298. eCollection 2015 May. PLoS Comput Biol. 2015. PMID: 26000633 Free PMC article. - Oncogenic extrachromosomal DNA functions as mobile enhancers to globally amplify chromosomal transcription.
Zhu Y, Gujar AD, Wong CH, Tjong H, Ngan CY, Gong L, Chen YA, Kim H, Liu J, Li M, Mil-Homens A, Maurya R, Kuhlberg C, Sun F, Yi E, deCarvalho AC, Ruan Y, Verhaak RGW, Wei CL. Zhu Y, et al. Cancer Cell. 2021 May 10;39(5):694-707.e7. doi: 10.1016/j.ccell.2021.03.006. Epub 2021 Apr 8. Cancer Cell. 2021. PMID: 33836152 Free PMC article. - Quantification of DNA cleavage specificity in Hi-C experiments.
Meluzzi D, Arya G. Meluzzi D, et al. Nucleic Acids Res. 2016 Jan 8;44(1):e4. doi: 10.1093/nar/gkv820. Epub 2015 Aug 11. Nucleic Acids Res. 2016. PMID: 26264668 Free PMC article. - Integrating epigenomic data and 3D genomic structure with a new measure of chromatin assortativity.
Pancaldi V, Carrillo-de-Santa-Pau E, Javierre BM, Juan D, Fraser P, Spivakov M, Valencia A, Rico D. Pancaldi V, et al. Genome Biol. 2016 Jul 8;17(1):152. doi: 10.1186/s13059-016-1003-3. Genome Biol. 2016. PMID: 27391817 Free PMC article. - Tracking the evolution of 3D gene organization demonstrates its connection to phenotypic divergence.
Diament A, Tuller T. Diament A, et al. Nucleic Acids Res. 2017 May 5;45(8):4330-4343. doi: 10.1093/nar/gkx205. Nucleic Acids Res. 2017. PMID: 28369658 Free PMC article.
References
- Dekker J, Rippe K, Dekker M, Kleckner N. Capturing chromosome conformation. Science. 2002;295:1306–1311. - PubMed
- Zhao Z, Tavoosidana G, Sjölinder M, Göndör A, Mariano P, Wang S, Kanduri C, Lezcano M, Sandhu KS, Singh U, et al. Circular chromosome conformation capture (4C) uncovers extensive networks of epigenetically regulated intra- and interchromosomal interactions. Nat. Genet. 2006;38:1341–1347. - PubMed
- Simonis M, Klous P, Splinter E, Moshkin Y, Willemsen R, de Wit E, van Steensel B, de Laat W. Nuclear organization of active and inactive chromatin domains uncovered by chromosome conformation capture-on-chip (4C) Nat. Genet. 2006;38:1348–1354. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases