Polygenic modeling with bayesian sparse linear mixed models - PubMed (original) (raw)
Polygenic modeling with bayesian sparse linear mixed models
Xiang Zhou et al. PLoS Genet. 2013.
Abstract
Both linear mixed models (LMMs) and sparse regression models are widely used in genetics applications, including, recently, polygenic modeling in genome-wide association studies. These two approaches make very different assumptions, so are expected to perform well in different situations. However, in practice, for a given dataset one typically does not know which assumptions will be more accurate. Motivated by this, we consider a hybrid of the two, which we refer to as a "Bayesian sparse linear mixed model" (BSLMM) that includes both these models as special cases. We address several key computational and statistical issues that arise when applying BSLMM, including appropriate prior specification for the hyper-parameters and a novel Markov chain Monte Carlo algorithm for posterior inference. We apply BSLMM and compare it with other methods for two polygenic modeling applications: estimating the proportion of variance in phenotypes explained (PVE) by available genotypes, and phenotype (or breeding value) prediction. For PVE estimation, we demonstrate that BSLMM combines the advantages of both standard LMMs and sparse regression modeling. For phenotype prediction it considerably outperforms either of the other two methods, as well as several other large-scale regression methods previously suggested for this problem. Software implementing our method is freely available from http://stephenslab.uchicago.edu/software.html.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
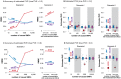
Figure 1. Comparison of PVE estimates from LMM (blue), BVSR (red), and BSLMM (purple) in two simulation scenarios.
The x-axis show the number of causal SNPs (Scenario I) or the number of medium/small effect SNPs (Scenario II). Results are based on 20 replicates in each case. (A) (true PVE = 0.2) and (C) (true PVE = 0.6) show RMSE of PVE estimates. (B) (true PVE = 0.2) and (D) (true PVE = 0.6) show boxplots of PVE estimates, where the true PVE is shown as a horizontal line. Notice a break point on the y-axis in (C).
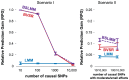
Figure 2. Comparison of prediction performance of LMM (blue), BVSR (red), and BSLMM (purple) in two simulation scenarios, where all causal SNPs are included in the data.
Performance is measured by Relative Predictive Gain (RPG). True PVE = 0.6. Means and standard deviations (error bars) are based on 20 replicates. The x-axis show the number of causal SNPs (Scenario I) or the number of medium/small effect SNPs (Scenario II).
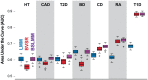
Figure 3. Comparison of prediction performance of LMM (blue), BVSR (red), and BSLMM (purple) for seven diseases in the WTCCC dataset.
Performance is measured by area under the curve (AUC), where a higher value indicates better performance. The order of the diseases is based on the performance of BSLMM. The mean and standard deviation of AUC scores for BSLMM in the seven diseases are 0.60 (0.02) for HT, 0.60 (0.03) for CAD, 0.61 (0.03) for T2D, 0.65 (0.02) for BD, 0.68 (0.02) for CD, 0.72 (0.01) for RA, 0.88 (0.01) for T1D.
Figure 4. Comparison of prediction performance of several models with BSLMM for three traits in the heterogenous stock mouse dataset.
Performance is measured by RMSE difference with respect to BSLMM, where a positive value indicates worse performance than BSLMM. The x-axis shows two different ways to split the data into a training set and a test set, each with 20 replicates. The mean RMSE of BSLMM for the six cases are 0.70, 0.80, 0.79, 0.90, 0.98 and 0.99, respectively.
Similar articles
- Fast and accurate Bayesian polygenic risk modeling with variational inference.
Zabad S, Gravel S, Li Y. Zabad S, et al. Am J Hum Genet. 2023 May 4;110(5):741-761. doi: 10.1016/j.ajhg.2023.03.009. Epub 2023 Apr 7. Am J Hum Genet. 2023. PMID: 37030289 Free PMC article. - Bayesian mapping of quantitative trait loci for complex binary traits.
Yi N, Xu S. Yi N, et al. Genetics. 2000 Jul;155(3):1391-403. doi: 10.1093/genetics/155.3.1391. Genetics. 2000. PMID: 10880497 Free PMC article. - A Bayesian model for detection of high-order interactions among genetic variants in genome-wide association studies.
Wang J, Joshi T, Valliyodan B, Shi H, Liang Y, Nguyen HT, Zhang J, Xu D. Wang J, et al. BMC Genomics. 2015 Nov 25;16:1011. doi: 10.1186/s12864-015-2217-6. BMC Genomics. 2015. PMID: 26607428 Free PMC article. - Single Marker Family-Based Association Analysis Not Conditional on Parental Information.
Namkung J, Won S. Namkung J, et al. Methods Mol Biol. 2017;1666:409-439. doi: 10.1007/978-1-4939-7274-6_20. Methods Mol Biol. 2017. PMID: 28980257 Review. - Bayesian joint modelling of longitudinal and time to event data: a methodological review.
Alsefri M, Sudell M, García-Fiñana M, Kolamunnage-Dona R. Alsefri M, et al. BMC Med Res Methodol. 2020 Apr 26;20(1):94. doi: 10.1186/s12874-020-00976-2. BMC Med Res Methodol. 2020. PMID: 32336264 Free PMC article. Review.
Cited by
- Application of Machine Learning to Ranking Predictors of Anti-VEGF Response.
Arslan J, Benke KK. Arslan J, et al. Life (Basel). 2022 Nov 18;12(11):1926. doi: 10.3390/life12111926. Life (Basel). 2022. PMID: 36431061 Free PMC article. - Accurate liability estimation improves power in ascertained case-control studies.
Weissbrod O, Lippert C, Geiger D, Heckerman D. Weissbrod O, et al. Nat Methods. 2015 Apr;12(4):332-4. doi: 10.1038/nmeth.3285. Epub 2015 Feb 9. Nat Methods. 2015. PMID: 25664543 - Pervasive correlations between causal disease effects of proximal SNPs vary with functional annotations and implicate stabilizing selection.
Zhang MJ, Durvasula A, Chiang C, Koch EM, Strober BJ, Shi H, Barton AR, Kim SS, Weissbrod O, Loh PR, Gazal S, Sunyaev S, Price AL. Zhang MJ, et al. Res Sq [Preprint]. 2023 Dec 15:rs.3.rs-3707248. doi: 10.21203/rs.3.rs-3707248/v1. Res Sq. 2023. PMID: 38168385 Free PMC article. Preprint. - The genetic architecture of gene expression levels in wild baboons.
Tung J, Zhou X, Alberts SC, Stephens M, Gilad Y. Tung J, et al. Elife. 2015 Feb 25;4:e04729. doi: 10.7554/eLife.04729. Elife. 2015. PMID: 25714927 Free PMC article. - Genetic architecture of gene expression traits across diverse populations.
Mogil LS, Andaleon A, Badalamenti A, Dickinson SP, Guo X, Rotter JI, Johnson WC, Im HK, Liu Y, Wheeler HE. Mogil LS, et al. PLoS Genet. 2018 Aug 10;14(8):e1007586. doi: 10.1371/journal.pgen.1007586. eCollection 2018 Aug. PLoS Genet. 2018. PMID: 30096133 Free PMC article.
References
- Yu J, Pressoir G, Briggs WH, Bi IV, Yamasaki M, et al. (2006) A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat Genet 38: 203–208. - PubMed
Publication types
MeSH terms
Grants and funding
- HG02585/HG/NHGRI NIH HHS/United States
- R01 HL092206/HL/NHLBI NIH HHS/United States
- 076113/WT_/Wellcome Trust/United Kingdom
- HL092206/HL/NHLBI NIH HHS/United States
- R01 HG002585/HG/NHGRI NIH HHS/United States
- U01 HL069757/HL/NHLBI NIH HHS/United States
- 085475/WT_/Wellcome Trust/United Kingdom
- WT_/Wellcome Trust/United Kingdom
LinkOut - more resources
Full Text Sources
Other Literature Sources