Estimating variable effective population sizes from multiple genomes: a sequentially markov conditional sampling distribution approach - PubMed (original) (raw)

Estimating variable effective population sizes from multiple genomes: a sequentially markov conditional sampling distribution approach

Sara Sheehan et al. Genetics. 2013 Jul.

Abstract

Throughout history, the population size of modern humans has varied considerably due to changes in environment, culture, and technology. More accurate estimates of population size changes, and when they occurred, should provide a clearer picture of human colonization history and help remove confounding effects from natural selection inference. Demography influences the pattern of genetic variation in a population, and thus genomic data of multiple individuals sampled from one or more present-day populations contain valuable information about the past demographic history. Recently, Li and Durbin developed a coalescent-based hidden Markov model, called the pairwise sequentially Markovian coalescent (PSMC), for a pair of chromosomes (or one diploid individual) to estimate past population sizes. This is an efficient, useful approach, but its accuracy in the very recent past is hampered by the fact that, because of the small sample size, only few coalescence events occur in that period. Multiple genomes from the same population contain more information about the recent past, but are also more computationally challenging to study jointly in a coalescent framework. Here, we present a new coalescent-based method that can efficiently infer population size changes from multiple genomes, providing access to a new store of information about the recent past. Our work generalizes the recently developed sequentially Markov conditional sampling distribution framework, which provides an accurate approximation of the probability of observing a newly sampled haplotype given a set of previously sampled haplotypes. Simulation results demonstrate that we can accurately reconstruct the true population histories, with a significant improvement over the PSMC in the recent past. We apply our method, called diCal, to the genomes of multiple human individuals of European and African ancestry to obtain a detailed population size change history during recent times.

Keywords: hidden Markov model (HMM); population size; recombination; sequentially Markov coalescent.

PubMed Disclaimer

Figures

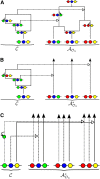
Figure 1

Figure 1

Illustration of a conditional genealogy C for a three-locus model. The three loci of a haplotype are each represented by a solid circle, with the color indicating the allelic type at that locus. Mutation events, along with the locus and resulting haplotype, are indicated by small arrows. Recombination events, and the resulting haplotype, are indicated by branching events. Absorption events are indicated by dotted horizontal lines. (A) The true genealogy AOn for the already observed sample O_n_. (B) Approximation by the trunk genealogy AOn*. Lineages in the trunk do not mutate, recombine, or coalesce. (C) Marginal conditional genealogy for each locus.

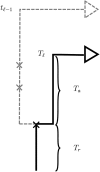
Figure 2

Figure 2

Illustration of the sequentially Markov approximation in which the absorption time _T_ℓ at locus ℓ is sampled conditionally on the absorption time _T_ℓ−1 = _t_ℓ−1 at the previous locus. In the marginal conditional genealogy Cℓ−1 for locus ℓ − 1, recombination breakpoints are realized as a Poisson process with rate ρ(ℓ−1,ℓ). If no recombination occurs, Cℓ is identical to Cℓ−1. If recombination does occur, as in the example here, Cℓ is identical to Cℓ−1 up to the time _T_r of the most recent recombination event. At this point, the lineage at locus ℓ, independently of the lineage at locus ℓ − 1, proceeds backward in time until being absorbed into a lineage of the trunk. The absorption time at locus ℓ is _T_ℓ = _T_r + _T_a, where _T_a is the remaining absorption time after the recombination event.

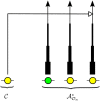
Figure 3

Figure 3

Illustration of the wedding-cake genealogy approximation, in which the varying thickness of a lineage in AOn* schematically represents the amount of contribution to the absorption rate. As shown, the wedding-cake genealogy never actually loses any of the n lineages, and absorption into any of the n lineages is allowed at all times; we are modifying the absorption rate only as a function of time.

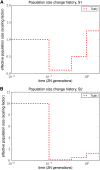
Figure 4

Figure 4

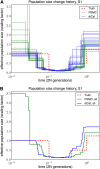
Population size histories considered in our simulation study, with time t = 0 corresponding to the present. (A) History S1 containing a bottleneck. (B) History S2 containing a bottleneck followed by a rapid expansion.

Figure 5

Figure 5

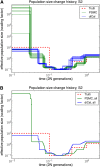
Results of PSMC and diCal on data sets simulated under history S1 with sample size n = 10 and four alleles (A, C, G, and T). PSMC significantly overestimates the most recent population size, whereas we obtain good estimates up until the very ancient past. (A) Results for 10 different data sets. (B) Average over the 10 data sets.

Figure 6

Figure 6

Results of PSMC and diCal on data sets simulated under history S2 with sample size n = 10 and four alleles (A, C, G, and T). The PSMC shows runaway behavior during the recent past, overestimating the most recent time by over three orders of magnitude on average. (A) Results for 10 different data sets. (B) Average over the 10 data sets.

Figure 7

Figure 7

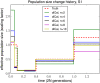
The effect of considering more haplotypes in diCal, using the SMCSD-based leave-one-out likelihood approach. Data were simulated under population size history S1 with two alleles. In this study, we grouped adjacent parameters to fit roughly with population size change points for illustration purposes. Shown is the increase in the accuracy of our method with an increasing sample size n. The recent sizes are the most dramatically affected, while intermediate sizes remain accurate even with few haplotypes.

Figure 8

Figure 8

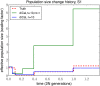
A comparison of the SMCSD-based leave-one-out likelihood approach in diCal, using the wedding-cake genealogy (blue line), with that using the unmodified trunk genealogy (green line). The results shown are for n = 10 haplotypes simulated under history S1 with two alleles. Without the wedding-cake genealogy, absorption of the left-out lineage into the trunk occurs too quickly, and the lack of absorption events in the midpast to the ancient past leads to substantial overestimation of the population sizes. Recent population sizes remain unaffected since during these times the absorption rates in the wedding-cake genealogy and in the trunk genealogy are roughly the same. In this example, we grouped adjacent parameters to fit roughly with population size change points for illustration purposes.

Figure 9

Figure 9

Estimated absorption times in diCal using the leave-one-out SMCSD method vs. the true coalescence times for a 100-kb region. The data were simulated using ms for n = 6 haplotypes, assuming a constant population size. The true coalescence time at each site, obtained from ms, was taken as the time the ancestral lineage of a left-out haplotype joined the rest of the coalescent tree at that site. Shown is the true coalescence time for the _n_th haplotype and our corresponding inferred absorption times, obtained from the posterior decoding and the posterior mean. Our estimates generally track the true coalescence times closely.

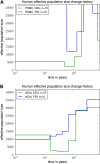
Figure 10

Figure 10

Variable effective population size inferred from real human data for European (CEU) and African (YRI) populations. For each population, we analyzed a 2-Mb region on chromosome 1 from five diploid individuals (10 haplotypes), assuming a per-generation mutation rate of μ = 1.25 × 10−8 per site. (A) The results of PSMC, which had some runaway behavior and unrealistic results. The data set is probably too small for PSMC to work accurately. (B) The results of diCal. We inferred that the European population size underwent a severe bottleneck ∼117 KYA and recovered in the past 16,000 years to an effective size of ≈12,500. In contrast, our results suggest that the YRI population size did not experience such a significant drop during the early out-of-Africa bottleneck phase in Europeans.

Similar articles

Cited by

References

    1. 1000 Genomes Project Consortium , 2010. A map of human genome variation from population-scale sequencing. Nature 467: 1061–1073. - PMC - PubMed
    1. Awadalla P., Gauthier J., Myers R., Casals F., Hamdan F., et al. , 2010. Direct measure of the de novo mutation rate in autism and schizophrenia cohorts. Am. J. Hum. Genet. 87: 316–324 - PMC - PubMed
    1. Chan A. H., Jenkins P. A., Song Y. S., 2012. Genome-wide fine-scale recombination rate variation in Drosophila melanogaster. PLoS Genet. 8(12): e1003090. - PMC - PubMed
    1. Coventry A., Bull-Otterson L. M., Liu X., Clark A. G., Maxwell T. J., et al. , 2010. Deep resequencing reveals excess rare recent variants consistent with explosive population growth. Nat. Commun. 1: 131. - PMC - PubMed
    1. Crawford D. C., Bhangale T., Li N., Hellenthal G., Rieder M. J., et al. , 2004. Evidence for substantial fine-scale variation in recombination rates across the human genome. Nat. Genet. 36: 700–706 - PubMed

Publication types

MeSH terms

LinkOut - more resources