Evolutionary dynamics of cancer in response to targeted combination therapy - PubMed (original) (raw)
doi: 10.7554/eLife.00747.
Johannes G Reiter, Benjamin Allen, Tibor Antal, Krishnendu Chatterjee, Preya Shah, Yo Sup Moon, Amin Yaqubie, Nicole Kelly, Dung T Le, Evan J Lipson, Paul B Chapman, Luis A Diaz Jr, Bert Vogelstein, Martin A Nowak
Affiliations
- PMID: 23805382
- PMCID: PMC3691570
- DOI: 10.7554/eLife.00747
Evolutionary dynamics of cancer in response to targeted combination therapy
Ivana Bozic et al. Elife. 2013.
Abstract
In solid tumors, targeted treatments can lead to dramatic regressions, but responses are often short-lived because resistant cancer cells arise. The major strategy proposed for overcoming resistance is combination therapy. We present a mathematical model describing the evolutionary dynamics of lesions in response to treatment. We first studied 20 melanoma patients receiving vemurafenib. We then applied our model to an independent set of pancreatic, colorectal, and melanoma cancer patients with metastatic disease. We find that dual therapy results in long-term disease control for most patients, if there are no single mutations that cause cross-resistance to both drugs; in patients with large disease burden, triple therapy is needed. We also find that simultaneous therapy with two drugs is much more effective than sequential therapy. Our results provide realistic expectations for the efficacy of new drug combinations and inform the design of trials for new cancer therapeutics. DOI:http://dx.doi.org/10.7554/eLife.00747.001\.
Keywords: None; cancer; genetics; mathematical biology; stochastic processes; targeted therapy.
Conflict of interest statement
The authors declare that no competing interests exist.
Figures
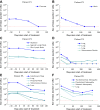
Figure 1.. Variability in treatment response to monotherapy among six patients.
Patients were treated with the BRAF inhibitor vemurafenib. Patients P1 and P2 achieved a complete response. Patient P3 had stable disease. Patients P4, P5, and P6 had partial responses. The minimal detection size (indicated by discontinuous red line) was assumed to be ≈63 × 106 cells. DOI:
http://dx.doi.org/10.7554/eLife.00747.003
Figure 2.. Tumor response to mono and dual therapy.
The tumor grows exponentially until a certain detection size, M, is reached, at which point treatment is initiated. The number of point mutations that could in principle confer resistance to monotherapy is n = 50. For dual therapy, the number of point mutations that could confer resistance to drugs 1 and 2 separately is given by _n_1 = 50 and _n_2 = 50. The number of point mutations that could confer resistance to both drugs simultaneously is given by _n_12. The point mutation rate was assumed to be u = 10−9 and the rate of cell division b = 0.14 per day and is unaffected by treatment. The rate of cell death before treatment is d = 0.13 per day; it is increased to _d_’ for sensitive cells during treatment. (A)–(C) For clinically detectable sizes (M = 1010, 109, 108, depending on the location of the tumors and the detection methods used), monotherapy leads to a temporary shrinkage of the tumor but is always followed by tumor regrowth. (D) Due to stochastic fluctuations the few resistant cells present at the start of treatment go extinct and the lesion is eradicated. (E) Treatment leads to a temporary shrinkage of the tumor followed by regrowth. (F) The tumor decreases slowly in response to dual therapy, but resistant cells eventually evolve and cause treatment failure. DOI:
http://dx.doi.org/10.7554/eLife.00747.005
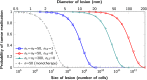
Figure 3.. Probability of tumor eradication for two-drug combination therapy.
A single mutation conferring cross-resistance to both drugs (_n_12 = 1) can prohibit any hope for a successful dual therapy. Solid curves show analytical results for dual therapy and dashed curve shows analytical results for a typical monotherapy, both are calculated using equation (1). Markers (square, triangle, circle, diamond) indicate simulation results (averages of 106 runs). Parameter values: birth rate b = 0.14, death rate d = 0.13, death rate for sensitive cells during treatment d’ = 0.17, point mutation rate u = 10−9. DOI:
http://dx.doi.org/10.7554/eLife.00747.006
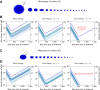
Figure 4.. Treatment response dynamics to monotherapy and dual therapy in two patients.
(A) Depiction of all 18 detectable metastases in patient N1, who had a particularly heavy tumor burden (scale 1:4). (B) Simulated treatment of patient N1, comparing monotherapy with n = 50 resistance mutations and dual therapy with _n_1 = _n_2 = 50 resistance mutations to the individual drugs and one (_n_12 = 1) or no (_n_12 = 0) cross-resistance mutations to both drugs. (C) Depiction of all 14 detectable metastases in patient N11, who had a more typical tumor burden (scale 1:4). (D) Simulated treatment of patient N11. Parameter values for simulations in (B) and (D): birth rate b = 0.14; death rate d = 0.13; death rate for sensitive cells during treatment _d_′ = 0.17; point mutation rate u = 10−9. DOI:
http://dx.doi.org/10.7554/eLife.00747.008
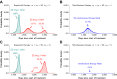
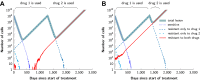
Figure 5.. Sequential vs simultaneous therapy with two drugs.
(A) If there is even a single mutation that confers cross-resistance to both drugs (_n_12 = 1), then sequential therapy will fail in all cases. In 73.7% of the cases, this failure is due to the exponential growth of fully resistant cells that were present at the start of treatment. In the remaining 26.3% of cases, the failure is due to resistance mutations that developed during therapy with the first drug. (B) With simultaneous therapy, 26.3% of patients can be cured under the same circumstances. In the remaining patients (73.7%), cross-resistant mutations existed prior to the therapy and their expansive growth will ensure treatment failure whether treatment is simultaneous or sequential (see Figure 5—figure supplement 1 for further details). (C) and (D) If the two drugs have no resistance mutations in common (_n_12 = 0), then simultaneous therapy is successful with a probability of 99.9% while sequential therapy still fails in all cases. DOI:
http://dx.doi.org/10.7554/eLife.00747.009
Figure 5—figure supplement 1.. Examples for the evolution of resistance during sequential therapy.
Two drugs are available for treatment where _n_1 = 50 and _n_2 = 50 point mutations confer resistance to each drug individually and one mutation confers resistance to both drugs simultaneously (_n_12 = 1). (A) A typical example of a tumor relapsing in the second wave of panel (A) in Figure 5. The few fully resistant cells go extinct due to stochastic fluctuations at the start of treatment. The cells resistant only to drug 1 produce cross-resistant cells during the treatment with the first drug. The cells resistant to both drugs received sequentially two mutations. (B) A typical example of a tumor relapsing in the first wave of panel (A) in Figure 5. The fully resistant cells are already present at the start of treatment. These cells received the cross-resistance mutation and are therefore immediately resistant to both drugs. The exponential growth of these fully resistant cells cause the relapse; their growth is unaffected by whether treatment is simultaneous or sequential. Parameter values: birth rate b = 0.14, death rate d = 0.13, death rate for sensitive cells during treatment d' = 0.17, point mutation rate u = 10−9, detection size of tumor (for start of treatment and relapse) M = N = 109 cells. DOI:
http://dx.doi.org/10.7554/eLife.00747.010
Comment in
- Targeted therapies: the maths behind combination therapy.
Kirk R. Kirk R. Nat Rev Clin Oncol. 2013 Sep;10(9):488. doi: 10.1038/nrclinonc.2013.131. Epub 2013 Jul 16. Nat Rev Clin Oncol. 2013. PMID: 23856749 No abstract available. - Cancer: calculated treatment.
Komarova NL, Boland CR. Komarova NL, et al. Nature. 2013 Jul 18;499(7458):291-2. doi: 10.1038/499291a. Nature. 2013. PMID: 23868257 Free PMC article.
Similar articles
- Evolutionary analysis of replicator dynamics about anti-cancer combination therapy.
Zhao R, Lai X. Zhao R, et al. Math Biosci Eng. 2023 Jan;20(1):656-682. doi: 10.3934/mbe.2023030. Epub 2022 Oct 13. Math Biosci Eng. 2023. PMID: 36650783 - Overcoming acquired BRAF inhibitor resistance in melanoma via targeted inhibition of Hsp90 with ganetespib.
Acquaviva J, Smith DL, Jimenez JP, Zhang C, Sequeira M, He S, Sang J, Bates RC, Proia DA. Acquaviva J, et al. Mol Cancer Ther. 2014 Feb;13(2):353-63. doi: 10.1158/1535-7163.MCT-13-0481. Epub 2014 Jan 7. Mol Cancer Ther. 2014. PMID: 24398428 - BRAF inhibitors in cancer therapy.
Hertzman Johansson C, Egyhazi Brage S. Hertzman Johansson C, et al. Pharmacol Ther. 2014 May;142(2):176-82. doi: 10.1016/j.pharmthera.2013.11.011. Epub 2013 Dec 8. Pharmacol Ther. 2014. PMID: 24325952 Review. - Stochastic modeling of drug resistance in cancer.
Komarova N. Komarova N. J Theor Biol. 2006 Apr 7;239(3):351-66. doi: 10.1016/j.jtbi.2005.08.003. Epub 2005 Sep 27. J Theor Biol. 2006. PMID: 16194548 - Vemurafenib.
Garbe C, Abusaif S, Eigentler TK. Garbe C, et al. Recent Results Cancer Res. 2014;201:215-25. doi: 10.1007/978-3-642-54490-3_13. Recent Results Cancer Res. 2014. PMID: 24756795 Review.
Cited by
- Accumulation of Oncogenic Mutations During Progression from Healthy Tissue to Cancer.
Zhang R, Bozic I. Zhang R, et al. Bull Math Biol. 2024 Oct 29;86(12):142. doi: 10.1007/s11538-024-01372-3. Bull Math Biol. 2024. PMID: 39472320 Free PMC article. - Tumor microenvironment governs the prognostic landscape of immunotherapy for head and neck squamous cell carcinoma: A computational model-guided analysis.
Bhattacharya P, Linnenbach A, South AP, Martinez-Outschoorn U, Curry JM, Johnson JM, Harshyne LA, Mahoney MG, Luginbuhl AJ, Vadigepalli R. Bhattacharya P, et al. bioRxiv [Preprint]. 2024 Sep 27:2024.09.26.615149. doi: 10.1101/2024.09.26.615149. bioRxiv. 2024. PMID: 39386511 Free PMC article. Preprint. - Neutral evolution of rare cancer mutations in the computer and the clinic.
Beckman RA. Beckman RA. NPJ Syst Biol Appl. 2024 Oct 2;10(1):110. doi: 10.1038/s41540-024-00436-3. NPJ Syst Biol Appl. 2024. PMID: 39358357 Free PMC article. Review. - Overcoming drug-resistant tumors with selection gene drives.
Wang H, Xie M. Wang H, et al. Cell Genom. 2024 Sep 11;4(9):100653. doi: 10.1016/j.xgen.2024.100653. Cell Genom. 2024. PMID: 39265528 Free PMC article. - Dissecting the Spatially Restricted Effects of Microenvironment-Mediated Resistance on Targeted Therapy Responses.
Miti T, Desai B, Miroshnychenko D, Basanta D, Marusyk A. Miti T, et al. Cancers (Basel). 2024 Jun 29;16(13):2405. doi: 10.3390/cancers16132405. Cancers (Basel). 2024. PMID: 39001467 Free PMC article.
References
- Antal T, Krapivsky PL. 2011. Exact solution of a two-type branching process: models of tumor progression. J Stat Mech 10.1088/1742-5468/2011/08/P08018 - DOI
- Athreya KB, Ney PE. 1972. Branching Processes. Berlin: Springer-Verlag
Publication types
MeSH terms
Grants and funding
- CA43460/CA/NCI NIH HHS/United States
- P30 CA008748/CA/NCI NIH HHS/United States
- N01-CN-43309/CN/NCI NIH HHS/United States
- CA129825/CA/NCI NIH HHS/United States
- CA57345/CA/NCI NIH HHS/United States
- R37 CA043460/CA/NCI NIH HHS/United States
LinkOut - more resources
Full Text Sources
Other Literature Sources