Transport of H2S and HS(-) across the human red blood cell membrane: rapid H2S diffusion and AE1-mediated Cl(-)/HS(-) exchange - PubMed (original) (raw)
Transport of H2S and HS(-) across the human red blood cell membrane: rapid H2S diffusion and AE1-mediated Cl(-)/HS(-) exchange
Michael L Jennings. Am J Physiol Cell Physiol. 2013.
Abstract
The rates of H2S and HS(-) transport across the human erythrocyte membrane were estimated by measuring rates of dissipation of pH gradients in media containing 250 μM H2S/HS(-). Net acid efflux is caused by H2S/HS(-) acting analogously to CO2/HCO3(-) in the Jacobs-Stewart cycle. The steps are as follows: 1) H2S efflux through the lipid bilayer and/or a gas channel, 2) extracellular H2S deprotonation, 3) HS(-) influx in exchange for Cl(-), catalyzed by the anion exchange protein AE1, and 4) intracellular HS(-) protonation. Net acid transport by the Cl(-)/HS(-)/H2S cycle is more efficient than by the Cl(-)/HCO3(-)/CO2 cycle because of the rapid H2S-HS(-) interconversion in cells and medium. The rates of acid transport were analyzed by solving the mass flow equations for the cycle to produce estimates of the HS(-) and H2S transport rates. The data indicate that HS(-) is a very good substrate for AE1; the Cl(-)/HS(-) exchange rate is about one-third as rapid as Cl(-)/HCO3(-) exchange. The H2S permeability coefficient must also be high (>10(-2) cm/s, half time <0.003 s) to account for the pH equilibration data. The results imply that H2S and HS(-) enter erythrocytes very rapidly in the microcirculation of H2S-producing tissues, thereby acting as a sink for H2S and lowering the local extracellular concentration, and the fact that HS(-) is a substrate for a Cl(-)/HCO3(-) exchanger indicates that some effects of exogenous H2S/HS(-) may not result from a regulatory role of H2S but, rather, from net acid flux by H2S and HS(-) transport in a Jacobs-Stewart cycle.
Keywords: AE1; erythrocyte; hydrogen sulfide; sulfide anion; transport.
Figures
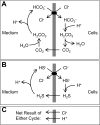
Fig. 1.
A: Jacobs-Stewart cycle for net efflux of acid. Starting at the top and going clockwise, the steps are as follows: 1) Cl−/HCO3− exchange, 2) intracellular HCO3− protonation and dehydration, 3) CO2 efflux, and 4) extracellular CO2 hydration and deprotonation. B: Jacobs-Stewart cycle for net efflux of acid mediated by Cl−/HS− exchange, intracellular HS− protonation, H2S efflux, and extracellular H2S deprotonation. C: net result of 1 cycle.
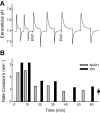
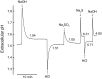
Fig. 2.
Effect of ethoxzolamide on rate of pH equilibration in human erythrocytes at 37°C and atmospheric CO2. Washed erythrocytes (1.75 ml) were suspended in 160 mM KCl buffered with 1 mM glycylglycine and 0.5 mM HEPES. Extracellular buffer power was 14 μmol/pH, and intracellular buffer power was 115 μmol/pH. A: pH vs. time. Each upstroke of the pH trace represents addition of 5 μmol of NaOH, and each downstroke represents addition of 5 μmol of HCl. Ethoxzolamide (EthZ, 10 μM) was added from a 10 mM stock solution in ethanol at each arrow. Final ethanol concentration was 0.2%. B: rate constants for pH equilibration calculated from pH transients over the range 0.07–0.02 unit from the final value. Point with error bars at right represents mean and range of rates of CO2-independent pH equilibration at pH 7.3–7.5 previously published (29) corrected to 37°C and the extracellular buffer power in the present experiment. Rate of pH equilibration in the presence of 20 μM ethoxzolamide is approximately equal to the CO2-independent rate.
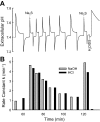
Fig. 3.
Stimulation of pH equilibration by addition of Na2S. Continuation of the experiment in Fig. 2. A: pH vs. time, with the last acid and base pulse in Fig. 2 repeated. Two upstrokes labeled Na2S represent addition of 5 μmol of Na2S from a 0.1 M stock solution that had been frozen until use. Other upstrokes and downstrokes represent additions of 5 μmol of NaOH and HCl, respectively. H2DIDS was added from a 5 mM stock solution to a final concentration of 10 μM. B: rate constants for pH equilibration calculated from the pH transients as described in Fig. 2 legend. In 4 experiments performed at equilibrium pH 7.35–7.45, the mean Na2S-stimulated rate constant for pH equilibration was 4.5 min−1 (range 3.9–5.5), measured immediately after the Na2S pulse.
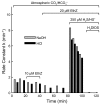
Fig. 4.
Rate constants for pH equilibration following NaOH or HCl pulses at equilibrium pH 8.4–8.45, 37°C, and atmospheric CO2 and with 160 mM KCl buffered with 1 mM glycylglycine and 0.5 mM HEPES. The first gray bar following the bracket labeled 250 μM H2S/HS− is the rate constant following a pulse of 5 μmol of Na2S rather than NaOH.
Fig. 5.
Lack of stimulation of pH equilibration by Na2SO3. Cells were suspended in weakly buffered 160 mM KCl as described previously, and 20 μM ethoxzolamide was added to inhibit CO2-dependent pH equilibration. The number adjacent to each pH transient is the rate constant (min−1) for relaxation of the transient. Each arrow represents addition of 5 μmol of the indicated acid, base, or salt. Na2SO3 does not cause as large a pH transient as Na2S, because SO32− is not as strong a base as S2−. Rate constant for relaxation of the transient could nonetheless be measured and is not detectably different from the rate constant following NaOH. As described previously, Na2S stimulates the rate of pH equilibration by ∼5 min−1, with the rate decaying with subsequent acid and base additions.
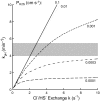
Fig. 6.
Rate constant (min−1) for sulfide-dependent pH equilibration predicted by the Jacobs-Stewart cycle plotted vs. rate constant _k_ex (s−1) for Cl−/HS− exchange for various values of the H2S permeability coefficient _P_H2S (cm/s). Predicted value of _k_pH was calculated as described in Modeling, with extracellular buffer power one-eighth of intracellular buffer power. Gray zone represents range of values of sulfide-dependent _k_pH at equilibrium pH 7.3–7.5 for the same buffer conditions (_k_pH = 3.9–5.5 min−1, 4 experiments). If _P_H2S is >0.001 cm/s, the observed rate is mainly limited by Cl−/HS− exchange and requires a Cl−/HS− exchange rate constant ≥2.5 s−1. If _P_H2S is <0.0003 cm/s, even a very high Cl−/HS− exchange rate could not explain the _k_pH at pH 7.4, because the cycle would be limited by H2S transport.
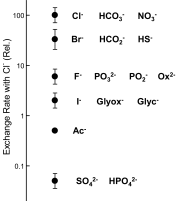
Fig. 7.
Relative Cl−/X− exchange rates for various inorganic and organic anions via mammalian AE1. Present data indicate that the Cl−/HS− exchange rate is about one-third that of Cl− and HCO3− and is comparable to that of Cl−/Br− exchange (19, 20, 64) and Cl−/formate exchange (23, 30). F−, I− (64), oxalate (Ox2−), glycolate (Glyc−), glyoxalate (Glyox−) (30), phosphate, phosphite, hypophosphite (16), acetate (Ac−) (18, 20), and sulfate (47) exchange for Cl− much more slowly.
Similar articles
- Cytosolic H+ microdomain developed around AE1 during AE1-mediated Cl-/HCO3- exchange.
Johnson DE, Casey JR. Johnson DE, et al. J Physiol. 2011 Apr 1;589(Pt 7):1551-69. doi: 10.1113/jphysiol.2010.201483. Epub 2011 Feb 7. J Physiol. 2011. PMID: 21300752 Free PMC article. - Deficient HCO3- transport in an AE1 mutant with normal Cl- transport can be rescued by carbonic anhydrase II presented on an adjacent AE1 protomer.
Dahl NK, Jiang L, Chernova MN, Stuart-Tilley AK, Shmukler BE, Alper SL. Dahl NK, et al. J Biol Chem. 2003 Nov 7;278(45):44949-58. doi: 10.1074/jbc.M308660200. Epub 2003 Aug 21. J Biol Chem. 2003. PMID: 12933803 - Mouse Ae1 E699Q mediates SO42-i/anion-o exchange with [SO42-]i-dependent reversal of wild-type pHo sensitivity.
Chernova MN, Stewart AK, Barry PN, Jennings ML, Alper SL. Chernova MN, et al. Am J Physiol Cell Physiol. 2008 Aug;295(2):C302-12. doi: 10.1152/ajpcell.00109.2008. Epub 2008 May 14. Am J Physiol Cell Physiol. 2008. PMID: 18480299 Free PMC article. - Cell physiology and molecular mechanism of anion transport by erythrocyte band 3/AE1.
Jennings ML. Jennings ML. Am J Physiol Cell Physiol. 2021 Dec 1;321(6):C1028-C1059. doi: 10.1152/ajpcell.00275.2021. Epub 2021 Oct 20. Am J Physiol Cell Physiol. 2021. PMID: 34669510 Free PMC article. Review. - Anion transport systems in the plasma membrane of vertebrate cells.
Hoffmann EK. Hoffmann EK. Biochim Biophys Acta. 1986 Jun 12;864(1):1-31. doi: 10.1016/0304-4157(86)90014-6. Biochim Biophys Acta. 1986. PMID: 3521744 Review.
Cited by
- S-sulfhydration as a cellular redox regulation.
Iciek M, Kowalczyk-Pachel D, Bilska-Wilkosz A, Kwiecień I, Górny M, Włodek L. Iciek M, et al. Biosci Rep. 2015 Nov 25;36(2):e00304. doi: 10.1042/BSR20150147. Biosci Rep. 2015. PMID: 26607972 Free PMC article. Review. - Green tea polyphenolic antioxidants oxidize hydrogen sulfide to thiosulfate and polysulfides: A possible new mechanism underpinning their biological action.
Olson KR, Briggs A, Devireddy M, Iovino NA, Skora NC, Whelan J, Villa BP, Yuan X, Mannam V, Howard S, Gao Y, Minnion M, Feelisch M. Olson KR, et al. Redox Biol. 2020 Oct;37:101731. doi: 10.1016/j.redox.2020.101731. Epub 2020 Sep 18. Redox Biol. 2020. PMID: 33002760 Free PMC article. - Red Blood Cell-Mediated S-Nitrosohemoglobin-Dependent Vasodilation: Lessons Learned from a β-Globin Cys93 Knock-In Mouse.
Premont RT, Reynolds JD, Zhang R, Stamler JS. Premont RT, et al. Antioxid Redox Signal. 2021 Apr 20;34(12):936-961. doi: 10.1089/ars.2020.8153. Epub 2020 Jul 23. Antioxid Redox Signal. 2021. PMID: 32597195 Free PMC article. Review. - The Reactive Species Interactome in Red Blood Cells: Oxidants, Antioxidants, and Molecular Targets.
Cortese-Krott MM. Cortese-Krott MM. Antioxidants (Basel). 2023 Sep 7;12(9):1736. doi: 10.3390/antiox12091736. Antioxidants (Basel). 2023. PMID: 37760039 Free PMC article. - The enzymatic function of the honorary enzyme: S-nitrosylation of hemoglobin in physiology and medicine.
Premont RT, Singel DJ, Stamler JS. Premont RT, et al. Mol Aspects Med. 2022 Apr;84:101056. doi: 10.1016/j.mam.2021.101056. Epub 2021 Nov 28. Mol Aspects Med. 2022. PMID: 34852941 Free PMC article. Review.
References
- Alper SL. The band 3 related anion exchanger gene family. Cell Physiol Biochem 4: 265–281, 1994 - PubMed
- Carrico RJ, Peisach J, Alben JO. The preparation and some physical properties of sulfhemoglobin. J Biol Chem 253: 2386–2391, 1978 - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous