Principles of regulation of self-renewing cell lineages - PubMed (original) (raw)
Principles of regulation of self-renewing cell lineages
Natalia L Komarova. PLoS One. 2013.
Abstract
Identifying the exact regulatory circuits that can stably maintain tissue homeostasis is critical for our basic understanding of multicellular organisms, and equally critical for identifying how tumors circumvent this regulation, thus providing targets for treatment. Despite great strides in the understanding of the molecular components of stem-cell regulation, the overall mechanisms orchestrating tissue homeostasis are still far from being understood. Typically, tissue contains the stem cells, transit amplifying cells, and terminally differentiated cells. Each of these cell types can potentially secrete regulatory factors and/or respond to factors secreted by other types. The feedback can be positive or negative in nature. This gives rise to a bewildering array of possible mechanisms that drive tissue regulation. In this paper, we propose a novel method of studying stem cell lineage regulation, and identify possible numbers, types, and directions of control loops that are compatible with stability, keep the variance low, and possess a certain degree of robustness. For example, there are exactly two minimal (two-loop) control networks that can regulate two-compartment (stem and differentiated cell) tissues, and 20 such networks in three-compartment tissues. If division and differentiation decisions are coupled, then there must be a negative control loop regulating divisions of stem cells (e.g. by means of contact inhibition). While this mechanism is associated with the highest robustness, there could be systems that maintain stability by means of positive divisions control, coupled with specific types of differentiation control. Some of the control mechanisms that we find have been proposed before, but most of them are new, and we describe evidence for their existence in data that have been previously published. By specifying the types of feedback interactions that can maintain homeostasis, our mathematical analysis can be used as a guide to experimentally zero in on the exact molecular mechanisms in specific tissues.
Conflict of interest statement
Competing Interests: The author has declared that no competing interests exist.
Figures
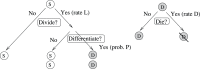
Figure 1. The schematic of cellular decisions and regulation by cell populations.
The circles marked with “S” and “D” denote stem and differentiated cells respectively. On the left, a stem cell decision tree is shown, which includes division/senescence decisions as well as proliferation/differentiation decisions. On top right, a differentiated cell decision tree is shown. All the decisions can be controlled by factors produced by the stem cell population and/or differentiated cell population. The control can be negative or positive in each case.
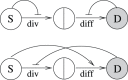
Figure 2. Minimal regulatory networks for a two-compartment system.
(a) Networks with two control loops. (b) Networks with three control loops. The circles marked with “S” and “D” denote stem and differentiated cells respectively. The two cell fate decisions are marked as “div” for divisions and “diff” for differentiation. Positive and negative bow-shaped arrows denote control loops.
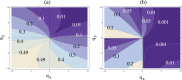
Figure 3. A graphical representation of stability conditions(4–5).
For fixed values of controls  and
and  , we identify the region of the
, we identify the region of the  space corresponding to stability of the stem cell system. The borders of this region are given by lines
space corresponding to stability of the stem cell system. The borders of this region are given by lines  and
and  . (a) Negative division controls:
. (a) Negative division controls:  ,
,  . (b) Positive division controls:
. (b) Positive division controls:  ,
,  . The parameter
. The parameter  .
.
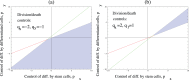
Figure 4. Stability and robustness of two-compartment control systems.
(a) For a wide range of positive and negative controls of the division,  and
and  , we show how robust the stability of the system is with respect to the choice of the controls of differentiation. The maximum robustness is
, we show how robust the stability of the system is with respect to the choice of the controls of differentiation. The maximum robustness is  (meaning that if we choose controls of differentiation
(meaning that if we choose controls of differentiation  and
and  randomly, with probability
randomly, with probability  we will get a stable solution). This corresponds to the lightest region in the south-west part of the diagram. The minimum robustness is zero, such that no choice of controls of differentiation will yield a stable solution. This corresponds to the darkest region in north-east part of the diagram. (b) Under the assumption of the connection between division and differentiation decisions, the same contour-plot is shown with the restriction
we will get a stable solution). This corresponds to the lightest region in the south-west part of the diagram. The minimum robustness is zero, such that no choice of controls of differentiation will yield a stable solution. This corresponds to the darkest region in north-east part of the diagram. (b) Under the assumption of the connection between division and differentiation decisions, the same contour-plot is shown with the restriction  ,
,  . The parameter
. The parameter  .
.
Figure 5. Minimal regulatory networks for a three-compartment system with three control loops.
(a) Left: the 7 networks containing (modifications of) the first pattern of figure 2(a). Right: the 7 networks containing (modifications of) the second pattern of figure 2(a). (b) The remaining 6 networks. Notations are similar to those of figure 2, with “I” denoting the intermediate cell type.
Similar articles
- Spatial dynamics of feedback and feedforward regulation in cell lineages.
Uhl P, Lowengrub J, Komarova N, Wodarz D. Uhl P, et al. PLoS Comput Biol. 2022 May 6;18(5):e1010039. doi: 10.1371/journal.pcbi.1010039. eCollection 2022 May. PLoS Comput Biol. 2022. PMID: 35522694 Free PMC article. - Determining the control networks regulating stem cell lineages in colonic crypts.
Yang J, Axelrod DE, Komarova NL. Yang J, et al. J Theor Biol. 2017 Sep 21;429:190-203. doi: 10.1016/j.jtbi.2017.06.033. Epub 2017 Jun 29. J Theor Biol. 2017. PMID: 28669884 Free PMC article. - Feedback regulation in multistage cell lineages.
Lo WC, Chou CS, Gokoffski KK, Wan FY, Lander AD, Calof AL, Nie Q. Lo WC, et al. Math Biosci Eng. 2009 Jan;6(1):59-82. doi: 10.3934/mbe.2009.6.59. Math Biosci Eng. 2009. PMID: 19292508 Free PMC article. - Interfollicular epidermal homeostasis: dicing with differentiation.
Doupé DP, Jones PH. Doupé DP, et al. Exp Dermatol. 2012 Apr;21(4):249-53. doi: 10.1111/j.1600-0625.2012.01447.x. Exp Dermatol. 2012. PMID: 22417300 Review. - Epidermal cell lineage.
Turksen K, Troy TC. Turksen K, et al. Biochem Cell Biol. 1998;76(6):889-98. doi: 10.1139/bcb-76-6-889. Biochem Cell Biol. 1998. PMID: 10392703 Review.
Cited by
- Spatial dynamics of feedback and feedforward regulation in cell lineages.
Uhl P, Lowengrub J, Komarova N, Wodarz D. Uhl P, et al. PLoS Comput Biol. 2022 May 6;18(5):e1010039. doi: 10.1371/journal.pcbi.1010039. eCollection 2022 May. PLoS Comput Biol. 2022. PMID: 35522694 Free PMC article. - Modelling stem cell ageing: a multi-compartment continuum approach.
Wang Y, Lo WC, Chou CS. Wang Y, et al. R Soc Open Sci. 2020 Mar 18;7(3):191848. doi: 10.1098/rsos.191848. eCollection 2020 Mar. R Soc Open Sci. 2020. PMID: 32269805 Free PMC article. - A modelling framework for cancer ecology and evolution.
Adler FR. Adler FR. J R Soc Interface. 2024 Jul;21(216):20240099. doi: 10.1098/rsif.2024.0099. Epub 2024 Jul 17. J R Soc Interface. 2024. PMID: 39013418 - Mathematical modeling of the impact of cytokine response of acute myeloid leukemia cells on patient prognosis.
Stiehl T, Ho AD, Marciniak-Czochra A. Stiehl T, et al. Sci Rep. 2018 Feb 12;8(1):2809. doi: 10.1038/s41598-018-21115-4. Sci Rep. 2018. PMID: 29434256 Free PMC article. - The Role of Symmetric Stem Cell Divisions in Tissue Homeostasis.
Yang J, Plikus MV, Komarova NL. Yang J, et al. PLoS Comput Biol. 2015 Dec 23;11(12):e1004629. doi: 10.1371/journal.pcbi.1004629. eCollection 2015 Dec. PLoS Comput Biol. 2015. PMID: 26700130 Free PMC article.
References
- Wu H, Ivkovic S, Murray R, Jaramillo S, Lyons K, et al. (2003) Autoregulation of neurogenesis by gdf11. Neuron 37: 197–207. - PubMed
- McPherron A, Lawler A, Lee S (1997) Regulation of skeletal muscle mass in mice by a new tgf-p superfamily member. Nature 387: 83–90. - PubMed
- Daluiski A, Engstrand T, Bahamonde M, Gamer L, Agius E, et al. (2001) Bone morphogenetic protein-3 is a negative regulator of bone density. Nature genetics 27: 84–88. - PubMed
- Yamasaki K, Toriu N, Hanakawa Y, Shirakata Y, Sayama K, et al. (2003) Keratinocyte growth inhibition by high-dose epidermal growth factor is mediated by transforming growth factor β au toinduction: A negative feedback mechanism for keratinocyte growth. Journal of investigative dermatology 120: 1030–1037. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources