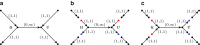Assembling single-cell genomes and mini-metagenomes from chimeric MDA products - PubMed (original) (raw)
. 2013 Oct;20(10):714-37.
doi: 10.1089/cmb.2013.0084.
Anton Bankevich, Dmitry Antipov, Alexey A Gurevich, Anton Korobeynikov, Alla Lapidus, Andrey D Prjibelski, Alexey Pyshkin, Alexander Sirotkin, Yakov Sirotkin, Ramunas Stepanauskas, Scott R Clingenpeel, Tanja Woyke, Jeffrey S McLean, Roger Lasken, Glenn Tesler, Max A Alekseyev, Pavel A Pevzner
Affiliations
- PMID: 24093227
- PMCID: PMC3791033
- DOI: 10.1089/cmb.2013.0084
Assembling single-cell genomes and mini-metagenomes from chimeric MDA products
Sergey Nurk et al. J Comput Biol. 2013 Oct.
Abstract
Recent advances in single-cell genomics provide an alternative to largely gene-centric metagenomics studies, enabling whole-genome sequencing of uncultivated bacteria. However, single-cell assembly projects are challenging due to (i) the highly nonuniform read coverage and (ii) a greatly elevated number of chimeric reads and read pairs. While recently developed single-cell assemblers have addressed the former challenge, methods for assembling highly chimeric reads remain poorly explored. We present algorithms for identifying chimeric edges and resolving complex bulges in de Bruijn graphs, which significantly improve single-cell assemblies. We further describe applications of the single-cell assembler SPAdes to a new approach for capturing and sequencing "microbial dark matter" that forms small pools of randomly selected single cells (called a mini-metagenome) and further sequences all genomes from the mini-metagenome at once. On single-cell bacterial datasets, SPAdes improves on the recently developed E+V-SC and IDBA-UD assemblers specifically designed for single-cell sequencing. For standard (cultivated monostrain) datasets, SPAdes also improves on A5, ABySS, CLC, EULER-SR, Ray, SOAPdenovo, and Velvet. Thus, recently developed single-cell assemblers not only enable single-cell sequencing, but also improve on conventional assemblers on their own turf. SPAdes is available for free online download under a GPLv2 license.
Figures
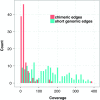
FIG. 1.
Coverage of chimeric and short genomic edges in the de Bruijn graph of the ECOLI-SC single-cell dataset (described in the Results section). The heights of red columns in the histogram give the number of occurrences of chimeric edges in the graph in each coverage bin. The heights of the blue columns give the number of occurrences of short (length less than n = 250) genomic edges in the graph in each coverage bin.
FIG. 2.
Example of breaking long edges in an assembly graph. (a) Subgraph of assembly graph where the four diagonal edges are long edges, while the horizontal edge in the center is not long. (b) Result of breaking the four long edges contains a connected component (in the center) with two sources (red vertices) and two sinks (blue vertices). The capacities of the edges starting (ending) at the newly formed sources (sinks) are inherited from the capacities of the broken edges. (c) Result of breaking long edges in a subgraph similar to the subgraph in (c) but with different directions on some edges.
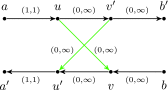
FIG. 3.
Interstrand edge (u, v) and its complementary edge, (_v_′, _u_′), both shown in green. The horizontal paths correspond to the two opposite DNA strands in a genome. Capacities are listed on each edge.
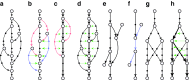
FIG. 4.
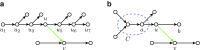
Illustration of bulge removal algorithms. For illustrative purposes, the vertices of the condensed graph are shown in white; the additional vertices present in the uncondensed graph are shown as small solid circles in the color (black, red, or blue) of the condensed edge on which they lie. Dotted green arrows indicate projection operations (not graph edges). (a–c) Algorithm A: The bulge corremoval algorithm from Bankevich et al. (2012). (a) A bulge in the de Bruijn graph. In (b), the blue edges have alternative paths while the red edges do not have alternative paths. After applying the bulge corremoval procedure to the blue edges, graph (b) is transformed into graph (c). There are now alternative paths for red edges in (c), and the graph is further transformed into a single condensed edge representing the bold path in (c). (e–f) Algorithm B: Merging paths instead of projecting paths. Merging two paths in (e) results in a graph (f) with an artificial (blue) path violating condition (ii). (g–h) Algorithm C: Blob corremoval. Complex bulge (g) is not removed by the bulge corremoval procedure from Bankevich et al. (2012). Applying the new “blob corremoval procedure” to blob (g) simplifies it via the projections shown in (h). Thick edges denote the tree to which we project the blob. The blob corremoval procedure may also be applied to (a) to directly simplify it to a single condensed edge in one step via the projections shown in (d); this achieves the same result as bulge corremoval did with two sets of projections, (b) and (c).
FIG. 5.
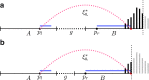
Observed insert length distribution between edges A and B of the assembly graph, given alignment positions pl and pr (left-most coordinates of left and right reads) and gap size g. Reads are shown in blue; in general, they can have different lengths, although on the Illumina platform, they have the same length. The insert length of this read pair goes from the start of the left read (pl) to the end of the right read (red point). A histogram of the full insert length distribution is shown on the right end of the figure; the black part of the histogram is observable while the gray part is unobservable due to finite edge length and the particular value of g. Edge B ends at the dotted vertical line, thus truncating the observable part of this histogram. Panels (a) and (b) illustrate different combinations of gap length and edge lengths, resulting in different portions of the distribution being observable.
FIG. 6.
(a) Edge (u, v) is classified as chimeric since it is a crossing edge for a critical cut. (b) Removal of edge (u, v) reveals a connected component C (after breaking long edges) with the number of incoming long edges exceeding the number of outgoing long edges by 1. This component reveals that (u, v) is a crossing edge in a critical cut.
FIG. 7.
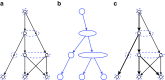
(a) Graph B. Vertices of the graph are iteratively removed and projected (with mapping g) to form a tree (b). Blue ellipses show groups of vertices that were projected onto the same vertex; g maps each vertex of B to the ellipse that contains it. (b) A representation of all skeleton trees of B. Each skeleton tree is formed by selecting one vertex of B from each ellipse and connecting the selected vertices by the same edges that connect the ellipses; these are not necessarily edges of B, however. (c) Thick edges denote a proper skeleton of graph B; this is a skeleton of B that is also a subtree of B. This was constructed by finding an embedding of panel (b) into graph B.
Similar articles
- SPAdes: a new genome assembly algorithm and its applications to single-cell sequencing.
Bankevich A, Nurk S, Antipov D, Gurevich AA, Dvorkin M, Kulikov AS, Lesin VM, Nikolenko SI, Pham S, Prjibelski AD, Pyshkin AV, Sirotkin AV, Vyahhi N, Tesler G, Alekseyev MA, Pevzner PA. Bankevich A, et al. J Comput Biol. 2012 May;19(5):455-77. doi: 10.1089/cmb.2012.0021. Epub 2012 Apr 16. J Comput Biol. 2012. PMID: 22506599 Free PMC article. - IDBA-UD: a de novo assembler for single-cell and metagenomic sequencing data with highly uneven depth.
Peng Y, Leung HC, Yiu SM, Chin FY. Peng Y, et al. Bioinformatics. 2012 Jun 1;28(11):1420-8. doi: 10.1093/bioinformatics/bts174. Epub 2012 Apr 11. Bioinformatics. 2012. PMID: 22495754 - Fragmentation and Coverage Variation in Viral Metagenome Assemblies, and Their Effect in Diversity Calculations.
García-López R, Vázquez-Castellanos JF, Moya A. García-López R, et al. Front Bioeng Biotechnol. 2015 Sep 17;3:141. doi: 10.3389/fbioe.2015.00141. eCollection 2015. Front Bioeng Biotechnol. 2015. PMID: 26442255 Free PMC article. - Sequence assembly using next generation sequencing data--challenges and solutions.
Chin FY, Leung HC, Yiu SM. Chin FY, et al. Sci China Life Sci. 2014 Nov;57(11):1140-8. doi: 10.1007/s11427-014-4752-9. Epub 2014 Oct 17. Sci China Life Sci. 2014. PMID: 25326069 Review. - Assessment of metagenomic assemblers based on hybrid reads of real and simulated metagenomic sequences.
Wang Z, Wang Y, Fuhrman JA, Sun F, Zhu S. Wang Z, et al. Brief Bioinform. 2020 May 21;21(3):777-790. doi: 10.1093/bib/bbz025. Brief Bioinform. 2020. PMID: 30860572 Free PMC article. Review.
Cited by
- Pathogenicity, phylogenomic, and comparative genomic study of Pseudomonas syringae sensu lato affecting sweet cherry in California.
Maguvu TE, Frias RJ, Hernandez-Rosas AI, Shipley E, Dardani G, Nouri MT, Yaghmour MA, Trouillas FP. Maguvu TE, et al. Microbiol Spectr. 2024 Oct 3;12(10):e0132424. doi: 10.1128/spectrum.01324-24. Epub 2024 Sep 3. Microbiol Spectr. 2024. PMID: 39225473 Free PMC article. - Cultivation and Genomics Prove Long-Term Colonization of Donor's Bifidobacteria in Recurrent Clostridioides difficile Patients Treated With Fecal Microbiota Transplantation.
Jouhten H, Ronkainen A, Aakko J, Salminen S, Mattila E, Arkkila P, Satokari R. Jouhten H, et al. Front Microbiol. 2020 Jul 15;11:1663. doi: 10.3389/fmicb.2020.01663. eCollection 2020. Front Microbiol. 2020. PMID: 32760391 Free PMC article. - First Draft Genome Sequence of Thermophilic Laceyella tengchongensis BKK01, Isolated from Municipal Solid Waste in Thailand.
Wachiralurpan S, Ruangsuj P, Yamprayoonswat W, Sopha P, Jumpathong W, Sittihan S, Kanjanavas P, Areekit S, Chansiri K, Chauyrod K, Yasawong M. Wachiralurpan S, et al. Microbiol Resour Announc. 2020 Sep 10;9(37):e00798-20. doi: 10.1128/MRA.00798-20. Microbiol Resour Announc. 2020. PMID: 32912914 Free PMC article. - Importance of Defluviitalea raffinosedens for Hydrolytic Biomass Degradation in Co-Culture with Hungateiclostridium thermocellum.
Rettenmaier R, Schneider M, Munk B, Lebuhn M, Jünemann S, Sczyrba A, Maus I, Zverlov V, Liebl W. Rettenmaier R, et al. Microorganisms. 2020 Jun 17;8(6):915. doi: 10.3390/microorganisms8060915. Microorganisms. 2020. PMID: 32560349 Free PMC article. - The Hypervariable Tpr Multigene Family of Theileria Parasites, Defined by a Conserved, Membrane-Associated, C-Terminal Domain, Includes Several Copies with Defined Orthology Between Species.
Palmateer NC, Munro JB, Nagaraj S, Crabtree J, Pelle R, Tallon L, Nene V, Bishop R, Silva JC. Palmateer NC, et al. J Mol Evol. 2023 Dec;91(6):897-911. doi: 10.1007/s00239-023-10142-z. Epub 2023 Nov 28. J Mol Evol. 2023. PMID: 38017120 Free PMC article.
References
- Aho A.V. Hopcroft J.E. Ullman J.D. Data Structures and Algorithms. Addison-Wesley Publishing Company; Boston: 1983.
- Blattner F.R. Plunkett G. Bloch C.A., et al. The complete genome sequence of escherichia coli K-12. Science. 1997;277:1453–1462. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
- R01 GM095373/GM/NIGMS NIH HHS/United States
- 3P41RR024851-02S1/RR/NCRR NIH HHS/United States
- 1R01GM095373/GM/NIGMS NIH HHS/United States
- 2R01HG003647/HG/NHGRI NIH HHS/United States
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials