Disentangling the effects of geographic and ecological isolation on genetic differentiation - PubMed (original) (raw)
. 2013 Nov;67(11):3258-73.
doi: 10.1111/evo.12193. Epub 2013 Jul 24.
Affiliations
- PMID: 24102455
- PMCID: PMC3808528
- DOI: 10.1111/evo.12193
Disentangling the effects of geographic and ecological isolation on genetic differentiation
Gideon S Bradburd et al. Evolution. 2013 Nov.
Abstract
Populations can be genetically isolated both by geographic distance and by differences in their ecology or environment that decrease the rate of successful migration. Empirical studies often seek to investigate the relationship between genetic differentiation and some ecological variable(s) while accounting for geographic distance, but common approaches to this problem (such as the partial Mantel test) have a number of drawbacks. In this article, we present a Bayesian method that enables users to quantify the relative contributions of geographic distance and ecological distance to genetic differentiation between sampled populations or individuals. We model the allele frequencies in a set of populations at a set of unlinked loci as spatially correlated Gaussian processes, in which the covariance structure is a decreasing function of both geographic and ecological distance. Parameters of the model are estimated using a Markov chain Monte Carlo algorithm. We call this method Bayesian Estimation of Differentiation in Alleles by Spatial Structure and Local Ecology (BEDASSLE), and have implemented it in a user-friendly format in the statistical platform R. We demonstrate its utility with a simulation study and empirical applications to human and teosinte data sets.
Keywords: Isolation by distance; isolation by ecology; landscape genetics; partial Mantel test.
© 2013 The Author(s). Evolution © 2013 The Society for the Study of Evolution.
Figures
Figure 1
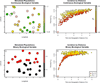
a) Populations simulated in the unit square, colored by their value of a continuous ecological variable. b) Pairwise FST between simulated populations from (a), colored by difference in their values of the continuous ecological variable. c) Populations simulated in the unit square, colored by their value of a binary ecological variable. d) Pairwise FST between simulated populations from (c), colored by difference in their values of the binary ecological variable.
Figure 2
Populations simulated using a spatially explicit coalescent model in the unit square. All simulated populations are indicated with black dots, while populations that were sampled for inclusion in each dataset are indicated by large black dots. All pairwise migration is indicated with gray arrows. The barrier to dispersal is given by the red dotted line, across which the standard migration rate was divided by a barrier effect size, which we varied.
Figure 3
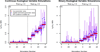
a) Performance of the method for the 100 datasets simulated with a continuous ecological distance variable. b) Performance of the method for the 100 datasets simulated with a binary ecological distance variable. In each, the left panel depicts performance on the 50 datasets for which α_E_ was fixed at 0, and the right panel depicts performance on the 50 datasets for which α_E_ varied.
Figure 4
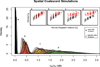
The marginal distributions on the α_E_/α_D_ratio from the analyses performed on the datasets simulated using a spatially explicit coalescent process. The migration rate between populations separated by the barrier was divided by a barrier effect size, which varied among simulations. Inset: Pairwise FST colored by whether populations were on the same or opposite sides of a barrier to dispersal, plotted against pairwise geographic distance for example datasets for each of the 4 barrier effect sizes. a) Barrier effect size of 1 (n=40); **b)**Barrier effect size of 5 (n=20); **c)**Barrier effect size of 10 (n=20); d) Barrier effect size of 15 (n=20).
Figure 5
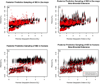
Posterior predictive sampling with 1,000 simulated datasets, using pairwise FST as a summary statistic of the allelic count data for: a) the Teosinte dataset, using the standard model; b) the Teosinte dataset, using the overdispersion model; c) HGDP dataset, standard model. d) HGDP dataset, overdispersion model.
Similar articles
- Using environmental correlations to identify loci underlying local adaptation.
Coop G, Witonsky D, Di Rienzo A, Pritchard JK. Coop G, et al. Genetics. 2010 Aug;185(4):1411-23. doi: 10.1534/genetics.110.114819. Epub 2010 Jun 1. Genetics. 2010. PMID: 20516501 Free PMC article. - Landscape genetic analyses reveal cryptic population structure and putative selection gradients in a large-scale estuarine environment.
McCairns RJ, Bernatchez L. McCairns RJ, et al. Mol Ecol. 2008 Sep;17(17):3901-16. doi: 10.1111/j.1365-294X.2008.03884.x. Epub 2008 Jul 24. Mol Ecol. 2008. PMID: 18662229 - A Markov chain Monte Carlo strategy for sampling from the joint posterior distribution of pedigrees and population parameters under a Fisher-Wright model with partial selfing.
Wilson IJ, Dawson KJ. Wilson IJ, et al. Theor Popul Biol. 2007 Nov;72(3):436-58. doi: 10.1016/j.tpb.2007.03.002. Epub 2007 Mar 12. Theor Popul Biol. 2007. PMID: 17448511 Review. - Analyses of genetic ancestry enable key insights for molecular ecology.
Gompert Z, Buerkle CA. Gompert Z, et al. Mol Ecol. 2013 Nov;22(21):5278-94. doi: 10.1111/mec.12488. Epub 2013 Sep 19. Mol Ecol. 2013. PMID: 24103088 Review.
Cited by
- Drivers of phenotypic divergence in a Mesoamerican highland bird.
Robles-Bello SM, Vázquez-López M, Ramírez-Barrera SM, Terrones-Ramírez AK, Hernández-Baños BE. Robles-Bello SM, et al. PeerJ. 2022 Feb 18;10:e12901. doi: 10.7717/peerj.12901. eCollection 2022. PeerJ. 2022. PMID: 35198262 Free PMC article. - Guiding seed movement: environmental heterogeneity drives genetic differentiation in Plathymenia reticulata, providing insights for restoration.
Conceição TA, Santos AS, Fernandes AKC, Meireles GN, de Oliveira FA, Barbosa RM, Gaiotto FA. Conceição TA, et al. AoB Plants. 2024 May 29;16(3):plae032. doi: 10.1093/aobpla/plae032. eCollection 2024 Jun. AoB Plants. 2024. PMID: 38883565 Free PMC article. - Maize diversity associated with social origin and environmental variation in Southern Mexico.
Orozco-Ramírez Q, Ross-Ibarra J, Santacruz-Varela A, Brush S. Orozco-Ramírez Q, et al. Heredity (Edinb). 2016 May;116(5):477-84. doi: 10.1038/hdy.2016.10. Epub 2016 Feb 24. Heredity (Edinb). 2016. PMID: 26905463 Free PMC article. - Phenotypic Variation in European Wild Pear (Pyrus pyraster (L.) Burgsd.) Populations in the North-Western Part of the Balkan Peninsula.
Vidaković A, Šatović Z, Tumpa K, Idžojtić M, Liber Z, Pintar V, Radunić M, Runjić TN, Runjić M, Rošin J, Gaunt D, Poljak I. Vidaković A, et al. Plants (Basel). 2022 Jan 27;11(3):335. doi: 10.3390/plants11030335. Plants (Basel). 2022. PMID: 35161316 Free PMC article. - A Spatial Framework for Understanding Population Structure and Admixture.
Bradburd GS, Ralph PL, Coop GM. Bradburd GS, et al. PLoS Genet. 2016 Jan 15;12(1):e1005703. doi: 10.1371/journal.pgen.1005703. eCollection 2016 Jan. PLoS Genet. 2016. PMID: 26771578 Free PMC article.
References
- Andrew RL, Ostevik KL, Ebert DP, Rieseberg LH. Adaptation with gene flow across the landscape in a dune sunflower. Molecular ecology. 2012;21:2078–2091. - PubMed
- Balding DJ. Likelihood-based inference for genetic correlation coefficients. Theoretical Population Biology. 2003;63:221–230. - PubMed
- Balding DJ, Nichols RA. A method for quantifying differentiation between populations at multi-allelic loci and its implications for investigating identity and paternity. Genetica. 1995;96:3–12. - PubMed
- Balding DJ, Nichols Ra. Significant genetic correlations among Caucasians at forensic DNA loci. Heredity. 1997;108:583–589. - PubMed
- Charlesworth B, Charlesworth D, Barton NH. The effects of genetic and geographic structure on neutral variation. Annual Review of Ecology, Evolution, and Systematics. 2003;34:99–125.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous