Opening and closing of a toroidal group II chaperonin revealed by a symmetry constrained elastic network model - PubMed (original) (raw)
Opening and closing of a toroidal group II chaperonin revealed by a symmetry constrained elastic network model
Hoomin Lee et al. Protein Sci. 2014 Jun.
Abstract
Recently, the atomic structures of both the closed and open forms of Group 2 chaperonin protein Mm-cpn were revealed through crystallography and cryo-electron microscopy. This toroidal-like chaperonin is composed of two eightfold rings that face back-to-back. To gain a computational advantage, we used a symmetry constrained elastic network model (SCENM), which requires only a repeated subunit structure and its symmetric connectivity to neighboring subunits to simulate the entire system. In the case of chaperonin, only six subunits (i.e., three from each ring) were used out of the eight subunits comprising each ring. A smooth and symmetric pathway between the open and closed conformations was generated by elastic network interpolation (ENI). To support this result, we also performed a symmetry-constrained normal mode analysis (NMA), which revealed the intrinsic vibration features of the given structures. The NMA and ENI results for the representative single subunit were duplicated according to the symmetry pattern to reconstruct the entire assembly. To test the feasibility of the symmetry model, its results were also compared with those obtained from the full model. This study allowed the folding mechanism of chaperonin Mm-cpn to be elucidated by SCENM in a timely manner.
Keywords: GroEL; chaperonin; elastic network interpolation; normal mode analysis; symmetric constrained elastic network model.
© 2014 The Protein Society.
Figures
Figure 1
The closed conformations of Mm-cpn in both the wild and lidless types. (A) Top and side views of Mm-cpn (upper: wild type, lower: lidless type). (B) A single subunit of each type is shown.
Figure 2
The identification of the hinge region. (A) The torsional angle difference between two models, 3IYF(open form) and 3J03(closed form). Because of the resolution difference between these two models (3IYF has a resolution of 4.8 Å, whereas 3J03 has a resolution of 8.0 Å), there exists substantial amount of noise. However, the significant angle difference in the figure indicates the existence of a hinge point in the intermediate domain. (B) Schematic of the torsion angle. It is defined as the angle between plane α (GLU 179-GLY 180-LYS 181) and plane β (GLY 180 –LYS 181- VAL 182). (C) A cartoon model of the wild type closed structure of Mm-cpn. The black arrow indicates the location of the hinge point (which is also highlighted via the space-filling model).
Figure 3
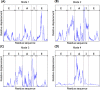
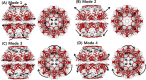
The normal mode shapes of in vitro Mm-cpn. Mode 1 to Mode 4 all show a general opening motion. However, in Modes 2 and 4 the opening motion occurs via a combination of axial motion and shear motion.
Figure 4
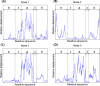
A comparison of the relative displacements of the in vitro (lidless) Mm-cpn, as predicted by SCNMA. The abbreviations “E,” “I,” and “A” represent the equatorial domain (residue numbers 1–135 and 373–491), the intermediate domain (residue numbers 136–212 and 318–372), and the apical domain (residue numbers 213–317), respectively.
Figure 5
The dominant mode shapes of in vivo Mm-cpn. A general opening motion is observed in Modes 1 through 4. Modes 2 and 3 show a simple opening motion, whereas Modes 1 and 4 indicate a breathing motion.
Figure 6
A comparison of the relative displacements of the in vivo (lidded) Mm-cpn, as predicted by symmetry constrained NMA. The abbreviations “E,” “I,” and “A” represent the equatorial domain (residue numbers 1–145 and 401–532), the intermediate domain (residue numbers 146–220 and 367–400), and the apical domain (residue numbers 221–366), respectively.
Figure 7
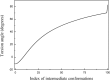
Torsion angle variation at the hinge point (Residues 179–180-181–182) throughout the conformational change from the closed to the open structure of lidless Mm-cpn. The smooth torsion angle change indicates a successful interpolation throughout the entire conformation index (0 to 100).
Figure 8
A diagram of the conformational change of chaperonin, as predicted by SCENI. The top and side views over the course of the transient pathway easily demonstrate its opening and breathing motions.
Figure 9
A schematic model of the chaperonin's structure. The area highlighted in red indicates a single subunit that was used for symmetry constrained ENM.
Figure 10
The formation of the reduced K matrix. Symmetry constraints were applied to both the individual subunit's interconnections and the intraconnections with neighboring subunits.
Similar articles
- Mechanism of folding chamber closure in a group II chaperonin.
Zhang J, Baker ML, Schröder GF, Douglas NR, Reissmann S, Jakana J, Dougherty M, Fu CJ, Levitt M, Ludtke SJ, Frydman J, Chiu W. Zhang J, et al. Nature. 2010 Jan 21;463(7279):379-83. doi: 10.1038/nature08701. Nature. 2010. PMID: 20090755 Free PMC article. - Crystal structures of a group II chaperonin reveal the open and closed states associated with the protein folding cycle.
Pereira JH, Ralston CY, Douglas NR, Meyer D, Knee KM, Goulet DR, King JA, Frydman J, Adams PD. Pereira JH, et al. J Biol Chem. 2010 Sep 3;285(36):27958-66. doi: 10.1074/jbc.M110.125344. Epub 2010 Jun 23. J Biol Chem. 2010. PMID: 20573955 Free PMC article. - The group II chaperonin Mm-Cpn binds and refolds human γD crystallin.
Knee KM, Goulet DR, Zhang J, Chen B, Chiu W, King JA. Knee KM, et al. Protein Sci. 2011 Jan;20(1):30-41. doi: 10.1002/pro.531. Protein Sci. 2011. PMID: 20981710 Free PMC article. - The Mechanism and Function of Group II Chaperonins.
Lopez T, Dalton K, Frydman J. Lopez T, et al. J Mol Biol. 2015 Sep 11;427(18):2919-30. doi: 10.1016/j.jmb.2015.04.013. Epub 2015 Apr 30. J Mol Biol. 2015. PMID: 25936650 Free PMC article. Review. - Chaperonins: two rings for folding.
Yébenes H, Mesa P, Muñoz IG, Montoya G, Valpuesta JM. Yébenes H, et al. Trends Biochem Sci. 2011 Aug;36(8):424-32. doi: 10.1016/j.tibs.2011.05.003. Epub 2011 Jun 30. Trends Biochem Sci. 2011. PMID: 21723731 Review.
Cited by
- Structure-Encoded Global Motions and Their Role in Mediating Protein-Substrate Interactions.
Bahar I, Cheng MH, Lee JY, Kaya C, Zhang S. Bahar I, et al. Biophys J. 2015 Sep 15;109(6):1101-9. doi: 10.1016/j.bpj.2015.06.004. Epub 2015 Jul 2. Biophys J. 2015. PMID: 26143655 Free PMC article. Review. - Fabrication and Characterization of Finite-Size DNA 2D Ring and 3D Buckyball Structures.
Jo S, Kim S, Lee BH, Tandon A, Kim B, Park SH, Kim MK. Jo S, et al. Int J Mol Sci. 2018 Jun 27;19(7):1895. doi: 10.3390/ijms19071895. Int J Mol Sci. 2018. PMID: 29954152 Free PMC article. - Disorder-Order Transitions in Conformational Selection of a Peptide by Ebola Virus Nucleoprotein.
Olson MA. Olson MA. ACS Omega. 2020 Mar 13;5(11):5691-5697. doi: 10.1021/acsomega.9b03581. eCollection 2020 Mar 24. ACS Omega. 2020. PMID: 32226846 Free PMC article.
References
- Young JC, Agashe VR, Siegers K, Hartl FU. Pathways of chaperone-mediated protein folding in the cytosol. Nat Rev Mol Cell Biol. 2004;5:781–791. - PubMed
- Horwich AL, Farr GW, Fenton WA. GroEL-GroES-mediated protein folding. Chem Rev. 2006;106:1917–1930. - PubMed
- Balch WE, Morimoto RI, Dillin A, Kelly JW. Adapting proteostasis for disease intervention. Science. 2008;319:916–919. - PubMed
- Bukau B, Horwich AL. The Hsp70 and Hsp60 chaperone machines. Cell. 1998;92:351–366. - PubMed
- Kubota H, Hynes G, Carne A, Ashworth A, Willison K. Identification of six Tcp-1-related genes encoding divergent subunits of the TCP-1-containing chaperonin. Cell. 1994;4:89–99. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials